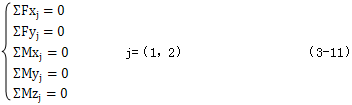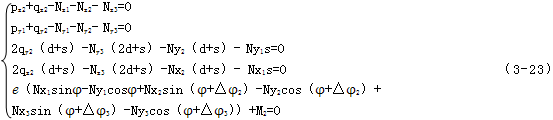3 机构受力分析
3.1 过约束机构的静不定次数
运动构件满足静定条件时，可按刚体力学原理进行分析。当机构中存在虚约束时，运动链不再满足静定条件，机构的受力分析无法由刚体力学的方法完全确定，这种机构称为静不定的约束机构，过约束机构的计算自由度小于实际自由度。
对于连杆行星齿轮传动机构，为了克服机构运动的不确定点，一般采用多相并列双曲柄平行四力形机构或多曲柄平行四边形机构作为输入机构，因此，它是多次静不定的过约束机构。要完全确定机构的约束反力，必须寻求与其静不定次数相同数目的位移协调补充方程。过约束机构的静不定次数与运动构件数、运动副类型及其数量等有关。对于少齿差连杆行星齿轮传动机构，由于轮齿的分担载荷大小与啮合数有关，机构的运转工况角以及构件的变形情况等因素有关，所以运动副数目也随之变化^{[34，35，29]}。

对于一个任意的空间机构，如果有n个运动构件，就能列出6n个动力分析方程，即可以求解确定6n个未知数。未知量的数量可以由以下两部分确定：即运动副中的约束反力未知分量与反力矩未知分量数，作用在输入构件上的输入力矩或输入力偶。一个运动副如沿某轴线有相对移动自由度，则沿该轴线的约束轴线的约束反力矩为零。因此，当一动动副的级别为K时，其约束反力的分量数为Pk，设每一输入构件上存在力或力偶，则输入构件上的未知力数为q，则未知量总数为：

当机构是静定系统时，未知量的总数应与基本方程式数目相等，即：

式（3-2）是机构自由度的计算公式。

当机构为过约束机构时，未知量的总数大于基本方程式数目相等，即：

将上式变为：

式（3-3）的左边为所有构件及运动副的计算自由度，右边q为实际自由度。设过约束机构的静不定闪数为S，由式（3-2）可得：

由此可知，当S=0时为静定机构，当S＞0时为静不定机构。

平面过约束机构得静不定次数可表示为：

式中P为低副数，t为高副数。
若一个多相多曲柄并列连杆行星传动机构有m根高速轴，n片行星齿扳，第i片行星齿板与输出外齿轮参加接触承载得齿对数为Z（i），则由工（3-4）求得其静不定次数为：

当m=2时，得多相并列双轴式得连杆行星齿轮传动机构得静不定次数

3.2 单个构件的位移协调原理

设一构件ab在外力的作用下产生微小位移（包含刚体位移和弹性变形位移），如图3.1所示。ab长为L，与水平坐标轴的夹角为θ₀，构件上a、b两点在受力后变位到a′，b′。作辅助线使：

由上图可得：

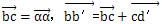
式中

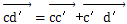
图3.1 构件变形位移关系

故：

式中：

用u、v分别表示点x、y方向的位 坐标分量，则式（3-5）写成坐标分量得：

由于构件得位移及变形很小，可取

所以

式中u_b，v_b是构件上b点的位移；

u_α，v_α是构件上α点的位移；

u_bα，v_bα是构件两点α、b的相对变形位移；

θ是构件上b点饶基点α的微小角位移。

式（3-6）是构件上任意两点的位移协调方程，其特理意义是：构件在外力作用下，产生微小刚体位移和弹性变形位移时，其上某点的位移是所选参考点的位移与该点饶参考点转动的角位移以及相对变形位移的合位移。

连杆上接触点b处受到的作用力Nx,Ny与接触点处的弹性变形量成正比，方向与变形方向相同，故

式中k：接触刚度系数

对于平行四边形双曲柄连杆机构，在外力的作用下，连杆B、C相对其理论位置产生一个微小位移，且在两端较链点B、C的接触处产生弹性变形。了B点为参考点，根据变形真调方程，在接触点C的变形量可表达如下：

上式中，（x_b，y_b）是B处的位移量，θ为连杆绕铰点的转角位移，β为接触点C在从动曲柄轴上绕轴线(D)的转角位移，L为连杆的长度，见图3.2。

图3.2 连杆接触点的变形关系

连杆上两端的作用反力与接触点处的弹性变形量成正比，因此可表达为：

式中（N_bx，N_by)、(N_cx，N_cy):连杆两端B、C的作用反力沿x轴、y轴的分量。

3.3 多相并列双曲柄机构动力分析模型
3.3.1 忽略质量时受力数学模型

图3.3是一多相并列双曲柄机构的结构简图，曲柄轴为输入轴，其上作用有已知外力F₁和未知输入力矩T₁，曲柄轴为支撑轴，其上的外力知T2和外力F₂以及作用在连杆B₁C₁上的合外力F_n1，外力矩M₁都是已知的，在任一时刻t，连杆A₁B₁与XOZ平面的夹角为φ₁，运用机构静态力学分析方法^{[22、29、30、34]}，对连杆B₁C₁可列出受力平衡方程：

共可列出3n 个方程。

图3.3 多相并列双曲柄机构的结构简图

而两曲柄轴上的力系为空间力系，其平衡方程为：

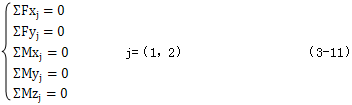
共可列出10个方程，联立式（3-10）或（3-11），对于多相并列双曲柄结构，用一般静态力学分析方法，可列出3n+10个方程，而未知量的总数为4n+9（运动副反力和输入力矩），故机构中未知量，（n-1）正是机构中的虚约束个数，为了得到补充方程，必须考虑构件的变形协调要求。

根据公式（3-9），每个环板可建立4个方程，那么n个环板可建立的方程总数为4n，式中位移量x_bi,y_bi,θ_i和β都是未知量，其总数为3n+1，故能提供的补充方程数为4n+3n-1=n-1个，同机构所包含的虚约束个数相等，联立式（3-10）、（3-11）、（3-9）可解得全部未知量。为了简化计算过程，可以利用结构力学中求解静定结构的位移计不，即把式（3-9）代入式（3-10）中，得到以连杆参数点位移x_bi,y_bi,θ_i和曲柄位移β为未知量的3n个方程，再由式（3-11）得到位移变形量B_xi，B_yi,θ_i, β为未知量的3n+1个方程，并从中解得各位移变量，然后代入式（3-11）、（3-9）中可求得机构各运动副反力及力矩。

把一个三相并列双曲柄机构作为一般情况进行受力分析，建立相应的数学模型，然后分四种状况进行计算。图3.4是基本型（低速轴在中间，高速轴两侧布置）环板受力情况，左边的高速轴为输入轴，输入力知M，输入转速为n,中间带外摆线轮的为输出轴，右边的高速轴为中间轴（支撑轴），在齿板上以左边轴承孔中心B₁为坐标原点建立坐标系0-XYZ，输入曲轴A₁B₁与X轴的夹角为φ。

在这里摆线针轮轮齿的受力情况作一个简化。因轮齿上受到的力均通过摆线轮的节圆上的一点，故可能所有轮齿受到的力简化成为一个合力，与摆线轮齿运动方向的夹角为α′（即啮合角）。见图3.4。

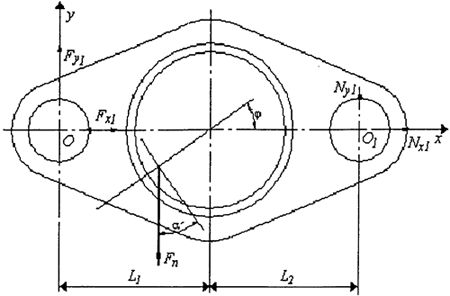
图3.4 连杆内齿轮的受力图

作用在输出轴摆线轮上的啮合力

式中：T——摆线轮上的扭矩（N·m）
r′_c——摆线轮节圆半径（mm）
α′——啮合角
P——输入轴输入功率（W）

n——输入轴转速（rpm）

t：环板参与啮合时的数量

由前面的分析可知，对A₁B₁C₁D₁双曲柄连杆机构，其平衡方程为：

式中：e——曲柄A1B1的长度。

如有多快环板，第二块与第一块的相位差为△φ₂，则有：

第三块与第一块的相位差为△φ₃

故齿板受力平衡方程：

式中：r_p′——针轮节圆半径。

那么中间轴的绕Z轴的力矩平平方程可写为：

e(Ny₁cosφ+Ny₂cos(φ+△φ₂)+Ny₃cos(φ+△φ₃)-Nx₁sinφ-Nx₂sin(φ+△φ₂)-Nx₃sin(φ+△φ₃) (3-20)

将工（3-15）～（3-20）代入式（3-19）～（3-20）可得到如下线性方程组：

[DIX]=[B] （3-21）

式中，[D]为系数矩阵：

式中：φ₁=φ；φ₂=φ+△φ₂；φ₃=φ+△φ₃。

[X]为变量阵：

[X]=[x_b1 y_b1 θ₁ x_b2 y_b2 θ₂ x_b3 y_b3 θ₃ β]^T

[B]为常数列阵：

图3.5是输入轴和支撑轴（中间轴）的受力图，不计自重及惯性力时，可得到高速轴的受力平衡方程。

图3.5 系统的受力图

输入轴：

中间轴：

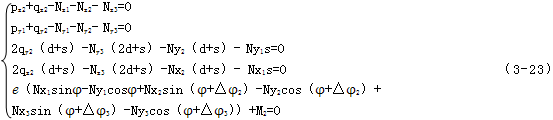
式中，d：环板与环板间的水平距离；

s：环板与箱体技撑轴承的水平距离；

p_x1，q_x1：主动高速轴支撑轴承的水平受力；

p_x2，q_x2：从动高速轴支撑轴承的水平受力。

3.3.2 考虑质量时受力数学模型

在常规情况L1=L2时，考虑质量时，力学模型中多了重力和惯性力，其数学模型可将式（3-19）改变为式（3-24），即：

当对两相平行轴摆线针轮减速器求解时，△φ₂=180，第三块环板因每输出扭矩，其相应的Fn=0；而对三相平行轴摆线针轮减速器，△φ₂=120，△φ₃=240。

3.4 不同结构平行轴摆线针轮减速器的受力分析
在不作特殊说明时，以下的受力分析是基于给定的条件：要率p=15kw，输入转速n=1500rpm，速比i=17，偏心距e=5,啮合角α=30°。
3.4.1连杆式两相平行轴摆线针轮减速器的受力分析
1）环板行星轴承的载荷情况
图3.6、图3.7给出了输入轴、从动轴环板行星与连杆轴承的载荷在一个循环周期内变化情况，其最大载荷及相应的位置见表3.1。
表3.1 环板行星与连杆轴承的最大载荷与位置

	沿x轴分力（N）		沿y轴分力（N）		合力（N）
	最大值	位置（°）	最大值	位置（°）	最大值	位置（°）
输入轴上环板1 轴承的受力F1	10248.4	117	7968.58	30	10882	93
输入轴上环板2 轴承的受力F2	10248.4	297	7968.58	210	10882	273
输入轴上连杆轴 承的受力F3	9549	180	0		9549	180
从动轴上上环板 1轴承的受力N1	3908.88	204	7968.58	210	8857.88	206
从动轴上上环板 2轴承的受力N2	3908.88	24	7968.58	30	8857.88	26
从动轴上连杆轴 承的受力N3	9549	180，0	0		9549	180，0

由表3.1可知，环板1与环板2上轴承的载荷 呈正弦分布，不论输入轴还是从动员，峰值的位置相差180°（即297-117，273-93，204-24，206-26），与它们在结构上的相位差相吻合；从动轴上连杆轴承的受力也呈正弦变化，在φ=180k(k=0,1,2...)时达到最大值，此时，正是环板1与环板2处于死点的位置，通过连杆使机构连续旋转。输入轴轴承上载荷峰值比从动轴的值大，连杆轴承的载荷介于两者之间。

2）箱体轴承的载荷情况
图3.8、3.9给出了输入轴、从动轴与箱体相联轴承的载荷在一个循环周期内变化情况，其最大载荷及相应的位置见表3.2。
表3.2 箱体轴承的最大载荷与位置

由图3.8、图3.9及表3.2可知，靠近联轴器侧的箱体轴承的载荷比另一侧的大，输入轴的箱体轴承的受力比从动轴的箱体轴承的大近50%。

3）啮合角对轴承载荷的影响
见图3.10与3.12。随着啮合角的增大，环板行星轴承的载荷增大，因此摆线针轮啮合力的合矢角度不谊太大（小于40°）；但啮合角的变化对连杆轴承的载荷的影响甚小。
4）仿主距对轴承载荷的影响

见图3.11与图3.13。随着偏心距增大，环板行星轴承的载荷和连杆轴承的载荷几乎成线性减少，因此不受体积限制时，应尺可能增加偏心距。

5）连杆机构中曲柄相位角对轴承载荷的影响

见图3.14、图3.15及图3.6。随着连杆机构中曲柄相位角增大，环板行星轴承的载荷和连杆轴承的载荷呈下降的趋势，但环板行星轴承沿y矢的载荷基本不受影响；大约在小于45°范围时，连杆轴承的载荷大于环板行星轴承的载荷，否则相反。因此取连杆机构曲柄与环板曲柄机构的曲柄相位差为90°最佳。

3.3.2 皮带轮式两相平行轴摆线针轮减速器的受力分析

所谓皮带轮式两相平行轴摆线针轮减速器，是指上属的连杆机构由齿形皮带传动取代。图3.17给出了输入轴环板行星与皮带轮轴承的载荷在一个循环周期内变化情况，其最大载荷及相应的位置见表3.3。由表3.3可知，环板上轴承的载荷以2π为周期进行变化，载荷峰值的位置相差180°（即288-108，271-91，360-180，206-26），与它们在结构上的相位差相吻合；皮带轮上的受力以π/2为周期进行变化，最大值所在位置介于环板上轴承的载荷的最大与最小时的相位之间，不是位于φ=180k（k=0，1，2...）。输入轴轴承上载荷峰值比从动轴的大，皮带轮上轴承的载荷介于两者之间。

表3.3 环板行星与连杆轴承的最大载荷与位置

	沿x轴分力（N）		沿y轴分力（N）		合力（N）
	最大值	位置（°）	最大值	位置（°）	最大值	位置（°）
输入轴上环板1 轴承的受力F1	9938.90	288	3057.66	32	10880.06	271
输入轴上环板2 轴承的受力F2	9938.90	108	3057.66	212	10880.06	91
输入轴上连杆轴 承的受力F3	7594.93	146	0		7594.93	56
从动轴上上环板 1轴承的受力N1	2756.56	360	7968.58	32	8332.03	26
从动轴上上环板 2轴承的受力N2	2756.56	180	7968.58	210	8332.03	206
从动轴上连杆轴 承的受力N3	7594.93	146	0		7594.93	56

表3.4 箱体轴承的最大载荷与位置

由表3.4及计算结果可知，靠近皮带轮侧的箱体轴承的载荷经比另一侧的小，输入轴的箱体轴承的受力比从动轴的箱体轴承的小近10%。

由图3.18可知，与连杆式平行轴摆线针轮减速器一样，随着啮合角的增大，环板行星轴承的载荷和皮带轮的受力增大；由图3.19可知，随着偏心距增大，环板行星轴承的载荷几乎成线性减少，而皮带轮轴承的载荷基本保持不变。

上一页

下一页