第五章 RV减速器固有频率的研究
RV减速器主要用于机器人中，而机器人对高定位精度和低振动水平的要求非常严格，因此还必须考虑RV减速器的动态特性，将其振动限制到很低的水平。为此，本课题利用有限元分析软件ANSYS对减速器的固有频率进行了研究，分析其振动是否达到要求。
5.1结构振动分析理论
减速器主要由机架、齿轮、轴、轴承等元件组成，对于此类系统，在内部和外部激励下将发生机械振动。振动系统的固有特性，一般包括固有频率和振型，它是系统的动态特性之一，对系统的动态响应、动载荷的产生与传递以及系统振动的形式等具有重要的影响。而结构在动载荷作用下所表现出来的动态特性是结构动力学的基本任务。
结构动力学中常用的分析模型是集中参数模型，集中参数模型是用常微分方程来描述的，而在集中参数模型中最常用的是有限元模型

其中，M、c、K分别为总体质量矩阵、阻尼矩阵和刚度矩阵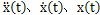，为结构的加速度向量、速度向量和为位移向量，f(t）为结构的激振力向量。

若无外力作用，即f(t)=0，则得到系统的自由振动方程。在求结构自由振动的频率和振型即求结构的固有频率和固有振型时，阻尼对它们影响不大，因此，阻尼项可以略去，这时无阻尼自由振动的运动方程为

此时系统存在n个固有频率和n个主振型。每一对频率和振型代表一个单自由度系统的自由振动。这种在自由振动时结构所具有的基本振动特性称为结构的模态。多自由度系统的自由振动可以分解为n个单自由度的简谐振动的叠加，或者说系统的自由振动是n个固有模态振动的线性组合。这意味着多自由度系统一般说来不是作某一个固有频率的自由振动而是作多个固有频率的简谐振动的合成振动。
设多自由度系统自由振动中某一简谐振动形式的解为

凡是满足频率方程的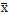和ω均代表该自由振动系统某一阶的基本振动特性，即系统的某一阶模态。求解式（5-6）得到n个特征值，特征值代表该系统的各阶固有频率固有频率具有如下特点：(l）固有频率仅和系统固有的质量和刚度有关而和外界激励无关，无阻尼系统的固有频率均是正实数；(2）固有频率是系统处在简谐振动时的频率，多自由度系统处于简谐振动是指多自由度系统的质点均处在简谐振动状态；(3）它们由小到大排列，即ω₁≤ω₂≤…≤ω_n。

将各阶固有频率ω_i，(i-l,2，…，n）依次代入方程式（5-6）便得到n个特征向量，即系统的n个主振型。主振型与固有频率是一

一对应的，不同的固有频率对应着不同的主振型。
5.2模态分析简介
结构动态设计要求根据结构的动载功况，根据对结构提出的功能要求及设计准则，按照结构动力学的分析方法和实验方法反复进行分析和计算，而结构模态分析是结构动态设计的核心。从物理方面看，模态表示其无阻尼自由振动时的各阶固有频率和主振型，它表明结构的共振频率以及在各阶频率下结构的相对变形。传统的动态分析只是在机器制成后在时域内测定机器有关结构的振动量，即选择若干测点测定其位移、速度及加速度随时间变化的曲线，这种方法不能直接了解系统的动态特性以及响应和结构之间的关系，因此既不能找出产生某种响应的原因，更不能在设计阶段就预见其动态特性。对比之下，模态分析的重要性显而易见。
对结构进行模态分析是ANSYS的强大功能之一。模态分析用于确定设计中的结构或机器部件的振动特性（固有频率和振型），其分析过程主要由四个步骤组成：
1.建模
建模过程中必须注意以下两点：
(l）在模态分析中只有线性行为是有效的，如果指定了非线性单元，将作为线性的来对待。
(2）材料性质可以是线性的或非线性的、各向同性的或正交各向异性的、恒定的或与温度相关的。在模态分析中必须指定弹性模量Ex（或某种形式的刚度）和密度DENS（或某种形式的质量），而非线性特性将被忽略。
2.加载及求解
(l）选择一种合适的模态提取方法。可选的模态提取方法有：
1)Subspace法（子空间法），该方法适用于大型对称特征值求解问题。可以用几种求解控制选项来控制子空间迭代过程。
2)Blook Lanozos法（分块的兰索斯法），适用于大型对称特征值求解问题。
3)PowerDynamics法，此方法适用于非常大的模型（100000个自由度以上），尤其适合于只求解结构前几阶模态，以了解结构将如何响应的情形，接着可以选择合适的提取方法（subspace或Block Lanczos）求得最终的解。
4）Reduced Householder法（豪斯霍尔德法），它比Subspace法快，但精度较低。
5）Unsymmetric法（非对称法）, 该方法适用于系统矩阵为非对称矩阵的问题，例如流体一结构相互作用问题。
6)Damped法，主要用于阻尼不可忽略的问题例如轴承问题。
在大多数分析过程中将选用Subspace法、Block Lanczos法、Reduced Householder法或PowerDynamics法，Unsymmetric法和Damped法只在特殊情形下才会用到，因此本课题中分别采用前两种方法进行了求解,得到相同的结果。
(2）在模型上加载荷。在典型的模态分析中唯一有效的“载荷”是零位移约束。如果在某个DOF处指定了一个非零位移约束，程序将以零位移约束替代在该DOF处的设置。对于其它类型的约束，如力、压力、温度、加速度等，可以在模态分析中指定，但在模态提取时将被忽略。
3.观察结果，结果包括固有频率和振型。
5.3 RV减速器有限元模型的建立及分析结果

将UG中的几何模型导入到ANSYS中，利用其AWE模块可自动地划分网格、施加接触。在对机械系统进行有限元分析时，所建立的模型在达到所要求分析精度的前提下应该尽量简单，这样可以节省计算时间，因此考虑到针齿壳与机物固结，不影响分析，建立有限元模型前将针齿壳去除。对于RV减速器选用八节点六面体实体单元来划分网格，共划分为56139个单元和97246个节点，划分网格后的有限元模型如图5-1所示。同时AWE模块根据所设定的接触检测的间隙误差（此处设为0），自动定义接触，之后在输入轴上施加固定约束，即可进行模态求解。利用AWE模块进行模态分析比传统的ANSYS进行模态分析过程简单、方便、所得结果也非常准确。

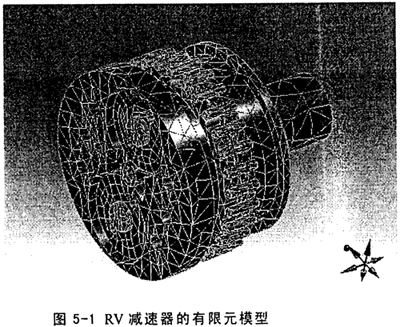
对上图有限元模型进行模态计算时不必求出全部的固有频率和振型，越是低价模态，对振动影响越大，通常取前5～10阶模态，精度就已足够。本课题在分析中求解了前11阶模态，这些模态的固频率和振型情况见表5-1，图5-2仅给出减速器的前6阶固有振型，通过振型图和各阶振型的动画显示，可直观地分析RV减速器的动态特性。

模态阶次	固有频率（Hz)	振型
1	836.42	输入轴水平摆动
2	841.39	输入轴垂直摆动
3	1300.58	刚性盘和输出盘扭转＋摆线轮扭转
4	4164.25	输入轴垂直弯曲
5	4403.56	输入轴水平弯曲
6	4882.55	输入轴轴向伸缩
7	8323.59	输入轴与渐开线齿轮水平摆动
8	9240.31	渐开线齿轮、曲柄轴及摆线轮扭转
9	9947.73	渐开线齿轮与曲柄轴摆动
10	10112.03	刚性盘与输出盘膨胀
11	10159.04	渐开线齿轮与曲柄轴摆动

表5-1 RV减速器的固有频率及振型表

在RV减速器的负载变化和误差较小的情况下，其激励就是啮合刚度的变化频率。RV减速器的啮合刚度由渐开线齿轮传动啮合刚度和摆线针轮传动啮合刚度组合而成，该系统的运动周期应是所包含的两种啮合刚度变化周期的最小公倍数，由于从输入齿轮轴到摆线轮的减速比很大，可以把摆线针轮啮合刚度变化的周期作为运动周期，其变化的频率为

f₂=n₂·（Z_b-1）/60 （5-7）

式中，n₂是第二级减速部分的输入转速。在额定功况下，输入轴转速为1500r/min，则n₂约为435r/min，这样得f₂=210.25Hz，由

5-1可以发现基叔远大于激励频率，因此RV减速器的振动水平很低，这也是RV减速器越来越广泛地应用于机器人的一个非常重要的原因。

上一页

下一页