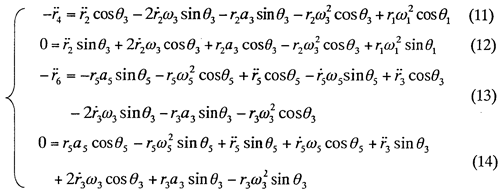第三章 运动学分析
本章中，从运动学角度入手分析柔性速度补偿装置的速度输出特性，对两自由度连杆机构用解析法作运动学分析，再借助Matlab软件来编程计算。运动学分析的结果将为下面的动力学分析提供理论依据。
§3.1引言
机械系统可以视为是由多个相互连接、彼此能够相互运动的构件的组合。
在机械系统设计中有3种性质不同的分析：
(l）机械系统的运动学分析
(2）机械系统的静力学分析
(3）机械系统的动力学分析
在本章中，暂不考虑系统的静力学分析，先从运动学分析入手，对柔性速度补偿装置进行分析研究。主要涉及系统及其各构件的运动分析，而与引起运动的力无关。运动学分析中，系统中一个或多个构件的位置或相对位置与时间的关系是规定好的，其余构件的位置、速度和加速度与时间的关系，可以通过求解位置的非线性方程组和速度、加速度的非线性方程组来确定。
本章所要做的工作就是对上一章选出来的二自由度连杆机构，进行运动学分析，初步选定机构的结构参数，分析其输入输出速度能否满足设计要求，为以后的动力学分析做依据。
§3.2Mat1ab软件
本章里，运动学分析中，有多组比较复杂的非线性方程要解，这些都是通过Matlab来实现的。
Mat1ab目前是大家比较常用的功能强大的数学计算软件，具有良好的开放性和运行的可靠性，在数值计算方面比较有优势。
本章所用的Matlab，是较新的6.5版本，是一种功能强、效率高、便于进行科学和工程计算的交互式软件包。其中包括：一般数值分析、矩阵运算、数字信号处理、建模、系统控制和优化等应用程序，并二集应用程序和图形于同一环境，便于使用。在此环境下，所解问题的Matlab语言表述形式和其数学形式相同，不需要按传统的方法编程。
对多数科学工作者而言，使用Matlab的库函数的可以节省很多重复编程，节省了大量的人力、物力和时间，加快了工作进程和效率。本章要借助Matlab软件编程来解方程。
§3.3运动学分析
平面机构运动分析的解析法也有多种，采用矢量方程解析法，比较便于应用和编程计算。
将图2-18所示的机构简图，按比例绘成运动简图，建立直角坐标系，按照矢量方程解析法，在图中标注各杆矢及其各杆矢的方位角。
对两自由度连杆机构，螺旋传动部分运动简单，不在这里做分析，本文主要针对其余的6杆机构构成的封闭链，进行分析计算，建立坐标如图3-1所示：

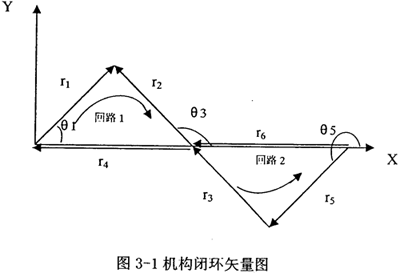
建立回路1矢量方程：

同理，建立回路2矢量方程：

对上述两个矢量方程式写成标量形式的方程式，如下：

同样，两边再对时间求导，整理，可得出加速度分析式：

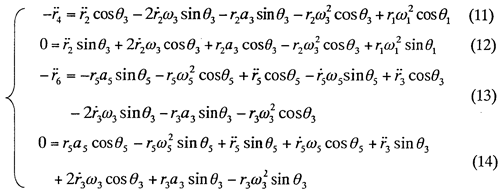
则同理，知：

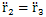
该机构本身是两自由度机构，但是在本文中，它须满足设计要求，即作为可调整机构，它在单自由度情况下，通过事先调整杆长比例，在第二输入不加的的时候，也可以达到比较理想的补偿效果，伺服电机电机驱动的第二输入是起补偿作用，微调杆长比例的。所以运动分析分两种情况，一种是单自由度下的运动状况，第二种是加入微调函数进行的运动分析。
第一种情况设曲柄输入角速度ω=1 rad/s，第二输入速度为零，这时相当于一个单自由度机构，螺旋传动未起作用。机构的结构在初始状态是完全对称的，运用matlab编程计算，得出运动分析结果，如图3-2所示。

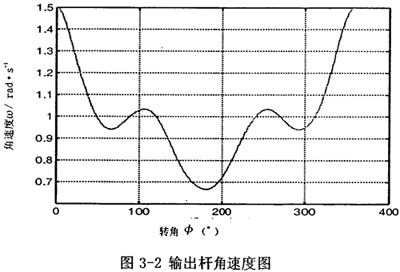
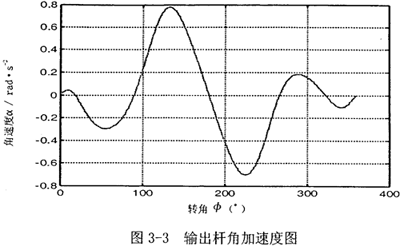
首先由图3-2可以看到，若机构结构参数设计恰当，并且调整中间滑块3偏移到合适的位置时，可在一定范围内，产生一个反向的速度波适度抵消原速度波动。再由图3-3可知，在未加入第二自由度时，加速度变化值不大，说明阻力矩和电机主动力矩不会受到大的影响，不致导致原机械系统的各项参数发生大的变化。
第二种情况 第一输入速度和第一种情况的速度值相同，现第二输入经螺旋机构转化为往复运动后，输入速度为v=sinθ₁（θ₁为第一输入角位移），即为滑块3的速度，再编程计算，得出结果如图3-4，图3-5所示。

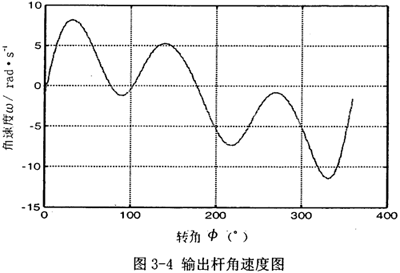
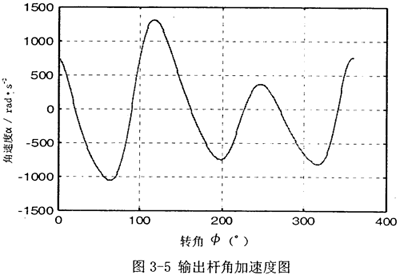
有上述图3-4和图3-5可知，引入第二自由度时，原速度波加速度波发生很大变化，这和第二自由度引入的驱动函数，有很大关系，所以应采用合理可行的控制函数，才能取得理想的速度输出。这将为后面的控制策略提供参考。
§3.4本章小节
本章对柔性速度补偿装置的机械机构，进行了运动学分析。借助Matlab计算软件编程解出了多组非线性方程，并分单自由度情况和两自由度情况给出速度和加速度图，可以直观的看到通过柔性速度补偿装置本身产生的速度波动来抵消机械运行中产生的速度波动，为后面章节的动力学分析提供理论依据。

上一页

下一页