工况2：加载时设置滑块3初始状况为从中间位置左移8mm，电机函数及其它参数不变，进行动力学仿真，其结果如秋4-15、图4-16所示。图中，纵轴上速度为负值，表示与输入轴曲柄速度方向相反。

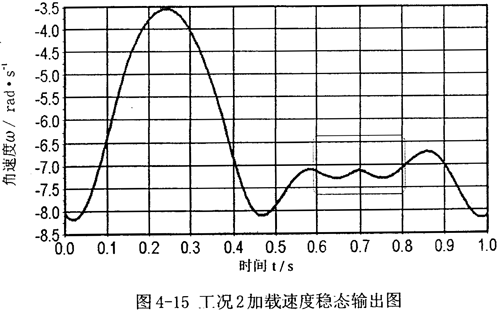
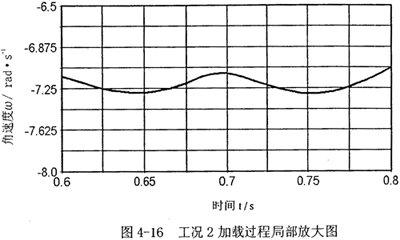
和工况上相比，工况2的负载特点不变，仍然是在一周期运动过程当中，加载的时段，载荷剧增。只是载荷的大小、位置，调节结构参数，仍然可以得到很好的速度补偿效果。
只是这种情况只在一定的载荷变化范围内，调节的是有效的，如果载荷变化大，超出允许的范围，该装置的补偿效果就不理想了。
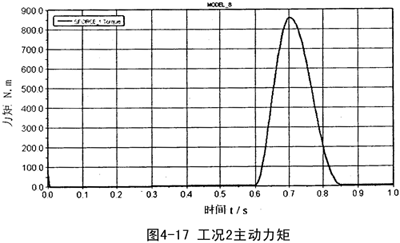
上述情况下邮电机力矩和岁载力矩的变化如图4-17、图4-18：

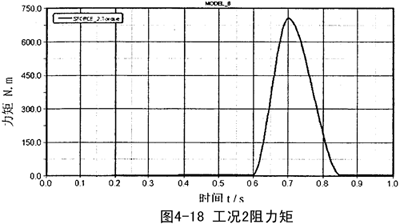
将上述两种工况下经柔性速度补偿装置速度补偿之后的数据分析计算如表4-3所示。

表4-3速度补偿前速度波动情况

工况1	ωmax=7.2969rad/s	ωmin=7.0178rad/s	δ1=0.0390
工况2	ωmax=6.0128rad/s	ωmin=5.7656rad/s	δ2=0.0420

以上两组数据分析表明，加载时，经柔性速度补偿装置速度补偿后的速度输出，在加载的时段，速度波动明显减小，具体数值可参看其局部放大图，另外，阻力矩和电机的主动力距和加柔性速度补偿装置前数值大小没有明显变化，表明对原机械系统的电机和其它动力、强度等一些性能参数没有大的影响。
两种工况下，δ均在不均匀系数许用值范围内，速度平稳，可见速度补偿装置的速度调节作用显著。
§4.3控制策略与第二阶段的速度补偿
本论文所研究的柔性速度补偿装置的设计思想是立足于传统机构学，强调以机构为主体，以控制为辅助，但也同时重视机构与控制的有机集成。因此选择合适的控制策略，和机构能很好的配合，才能完成所设计的速度调节。计算机具有的软件可调性为机器控制系统提供了柔性化和智能化的可能性，所以也是本论文极为重要的一环。
4.3.1选定控制方法
经分析，认为基于适度柔性机器理论的柔性速度补偿装置，其控制方式仍具有挑战性，这主要是因为：
(1）常速电机在系统的运转过程当中是不可控的。
(2）由伺服电机驱动的输入运动和常速电机驱动的输入运动是否能很好的耦合。
控制方式有多种，有经典的PID控制，也有现代的智能控制。经分析，并参考前人在该类机构控制方面所做的一些研究工作，决定系统采用学习控制（1eaming control）的方法。这也是由该柔性速度补偿装置本身的特点决定的：
(1）模型不确定。工作当中会因工作环境变化、磨损、受力受热等情况使工作情况发生变化，但这些变化无规律可循，只能靠控制来逐渐逼近期望输出。
(2)周期性。柔性速度补偿装置是以常速电机驱动的曲柄旋转一周为一周期的。
(3）需要控制简单、迅速，成本低。
依据这些这些特点，选择学习控制的方法作为柔性速度补置的控制方案。
学习控制是智能控制策略的一种。简单的说，由干对未知信息的估计逐步改善而导致控制性能的逐步改善，就是自学习控制。对学习控制的定义，不少学者给出了各自的见解:
Y.Z.Tsypkin把系统中的学习一词理解为一种过程，通过重复各输入信号并从外外部校正该系统，从而使系统对于特定的输入信号具有特定的响应。而自学习就是不具有外来校正的学习，或即不具有惩罚和奖励的学习。
G.N.Saridis认为，如果一个系统能对一个过程或其环境的未知特征所固有的信息进行学习，并将得到的经验用于进一步估计、分类、决策或控制，从而使系统的品质得到改善，那就称此系统为学习系统。
而学习系统将其得到的信息用于控制具有未知特征的过程，就成为学习主之制系统。
L.walter和J.A.farrell给出了比较完整、规范的学习控制表述是：一个学习控制系统是具有这样一种能力的系统，它能通过与控制对象和环境的闭环交互作用，根据过去获得的经验信息，逐步改进系统自身的未来性能。
这种表述说明了学习控制的一般特点：
(1)有一定的自主性。学习控制系统的性能是自我改进的；
(2)是一种动态过程。学习控制系统的性能随时间而变，性能的改进在与外界反复作用的过程中进行；
（3）有记忆功能。学习控制系统需要积累经验，用以改进其性能；
（4）有性能反馈。学习控制系统需要明确它的当前性能与某个目标性能之间的差距，施加改进操作。
学习控制有多种分类，本文采用基于迭代和重复的自学习控制。这类学习控制主要是针对在一定周期内作重复运动的系统，它不但与传统的控制理论相联系，而且可导出易于工程实现的学习控制规律。这正符合本课题的要求。
基于迭代和重复的自学习控制，其基本思想是针对一类特定的系统但又不依赖系统的精确数学模型，它通过反复训练的方式进行自学习，使系统逐步逼近期望的输出。控制作用的学习是通过对以往控制经验（控制作用与误差的加权和）的记忆实现的。算法的收敛性依赖于加权因子k的确定。这种学习系统的核心是系统不变性的假设以及基于记忆单元的间断的重复训练过程，因而不但有较好的实时性，而且对干扰和系统模型的变化具有一定的鲁棒性。
4.3.2控制算法
柔性速度补偿装置特征之一就是具有柔性、可控性功能。这一特征主要是靠控制器通过对伺服电机的实时在线控制来实现的，伺服电机是控制系统关键的执行元件。
系统的具体控制算法如下：
设ω₁、ω₂、ω₃、k分别为常速电机输入速度，伺服电机的输入速度，输出速度，理论输出速度（理想值）和加权因子，e为输出速度和理论输出速度值的误差范围。迭代周期以常速电机旋转一周（2π）为一周期，迭代进行一次。
则迭代过程如下：

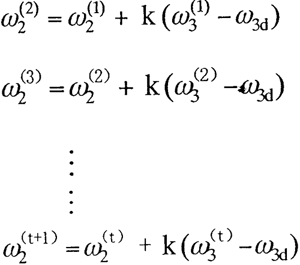
迭代直至判断式：δ=|ω₃^(t)-ω_3d|≤e。满足时，即说明该周期系统的误差收敛，则该周期终止，输出ω₃^(t)，然后进入下一轮迭代，依此循环下去。
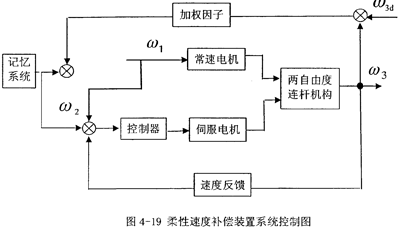
整个柔性速度补偿装置系统的控制方式如图4-19所示：

4.3.3第二阶段的速度补偿
第二阶段的速度补偿是在常速电机和控制器控制的伺服电机混合驱动的情形下，进行的动态仿真，是跟进一步的速度补偿。
依照此学习控制算法，第一输入还是采用上述等效力矩模型不变，然后设置第二自由度输入函数，再进行两自由度的动力学仿真分析，研究该柔性速度补偿装置的柔性功能和速度补偿效果。
由于控制的数学模型不确定，所以只能通过先给第二输入一个初始函数，比如三角函数，加权因子先给一个假设值，然后经两自由度机构输出一个速度波，根据算法和理想值比较，误差如果超出允许范围，计算机经计算给定第二步的输入函数，再进行速度补偿，取得第二个输出速度波……依次循环，逐步逼近理想输入函数。通过不断的调试，选择合适的加权因子，直到速度输入函数逐渐收敛为止，这样就得到了理想的第二输入速度函数。
迭代步骤如下：
初始设置加权因子k=10，ω₁=ω_3d=6.5rad/s，第一输入等效力矩模型和负载力矩模型依前述单自由度仿真建立。v₂为ω₂经螺旋传递装置转化为往复运动的速度。
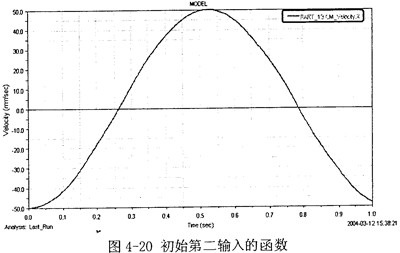
第一步：（1）给第二输入一个函数，假设V₂⁽²⁾=50cos(2πt)mm/s，如图4-20所示。

（2）在adams下建立的样机模型里，将上述速度值设置到第二输入中，设置好后，进行仿真。得到输出速度图4-21。

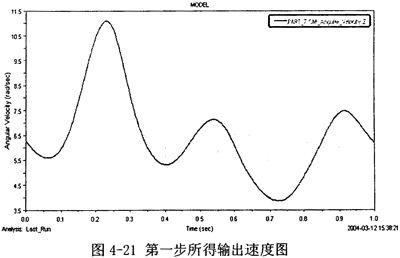
（3）将上述输出速度图每隔0.005秒采样一次，得到一组输出速度值的离散数据，以数据文件格式输出，如图4-22所示（图中只截取0.2秒内）。

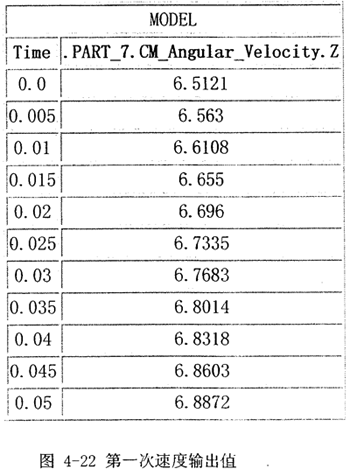
（4）将上述数据，形成一组输出速度函数ω₃⁽¹⁾，控制器调用学习控制算法，先根据判断式：

δ=|ω₃⁽¹⁾-ω_3d|≤e

判断是否超出许用值，在误差范围内。如果超出，用以下算式计算，

ω₂⁽²⁾=ω₂⁽¹⁾+K(ω₃⁽¹⁾-ω_3d)

得到新的一组ω₂⁽²⁾值，数据处理转化成平动速度，拟合形成3阶拟合曲线函数，如图4-23所示（实线为拟合曲线，下同）。

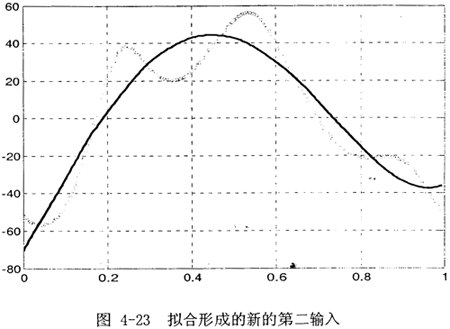
第二步：（1）将上述拟合的函数：作为新的第二输入函数：

V₂⁽²⁾=404.2t³-1023.2t²+652.6t-83.8

（2）在Adams下建立的样机模型里，将上述V2(2)速度函数设置到第二输入中，设置好后，进行仿真。得到输出速度曲线，如图4-24所示。

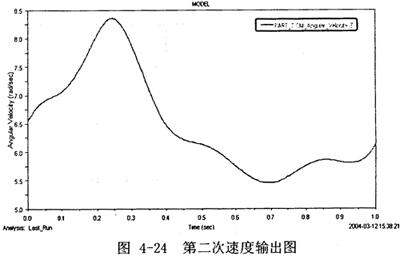
（3）同样，将上述输出速度图每隔0.005秒采样一次，得到一组输出速度值的离散数据，以数据文件格式输出，如图4-25所示（截取0.05秒内）。

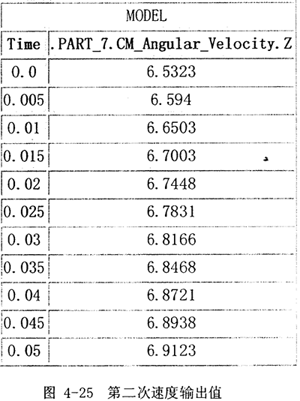
（4）将上述数据，形成一组输出速度函数ω₃⁽²⁾，控制器调用学习控制算法，先根据判断式：

δ=|ω₃⁽²⁾-ω_3d|≤e，

判断是否超出许用值，在误差范内。如果超出，用不以下算式计算，

ω₂⁽³⁾=ω₂⁽²⁾+K(ω₃⁽²⁾-ω_3d)

得到新一组ω₂⁽³⁾值，数据处理转化成平动速度，拟合形成3阶拟合函数曲线，如图4-26所示（图中实线为拟合函数）。

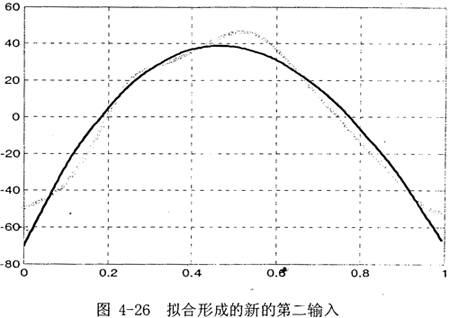
第n步：
依次类推，程序一周期迭代一次，直至得到符合要求的输出速度，最后得到一组理想的第二输入速度函数。
由于算法是用C语言编写的，它和Adams软件的接口技术问题一直没有很好的解决，导致上述过程事实上分两阶段手动完成的，就是先仿真得到输出速度曲线，然后将该曲线离散化输出到数据文件当中，然后在C语言环境下，调用该数据文件，编程处理计算出新的ω₂。所以这一部分没有实现完全的控制和仿真联合起来，导致无法得到一个收敛的ω₂函数和一个比较适合的加权因子k的值，很是遗憾。
§4.4本章小结
在本章中，经理论分析和仿真研究表明，该柔性速度补偿装置主要融合一些适度柔性机器原理，利用机构自身的运动特性，并通过伺服驱动系统的适度调整来调节速度的波动。
首先伺服电机不动作，该装置作为一个单自由度机构就可以补偿大部分的速度波动。然后，采用学习控制的方法作为该柔性速度补偿装置的控制策略。因为基于迭代的学习控制基本思想是针对一类特定的系统但又不依赖系统的精确数学模型，它通过反复训练的方式进行自学习，使系统逐步逼近期望的输出。在控制算法控制下伺服电机依据波动情况驱动第二输入，实现在两自由度机构和控制系统协同工作，最终为执行机构提供一个比较平稳的速度输入。
该补偿装置的主要特点是具有适度的柔性，可在一定范围内根据机械参数或运行工况的变化而进行相应调整。此外，其柔性还体现在对非加载时段的速度波动可根据需要选择是否进行补偿，不是全程速度补偿，从而适度降低补偿的代价。

上一页

下一页