第五章 三环减速器振动与噪声预估值分析与计算
§5-1 引言
在第三章中我们建立了三环减速器的数学模型,并对其理论建模进行了分析和计算,在第四章中我们又分析计算了Ⅱ子模型在各种工况下所受的激励力,这样我们就可以对三环减速机理论模型进行动态特性及响应计算了。主要计算Ⅱ子模型表面的振动速度用于表征、三环减速器噪声发射的预估值。
§5-2 振动与噪声
噪声来源于振动。运动着的机械必然产生振动,而机械噪声大部分是由于工程机械的振动而辐射的。
在对声场作出如下两点假设:
1、假设声场介质是理杨的流体介质。所谓的理想是认为介质运动过程中没有能量损耗。
2、假设介质是连续的。在讨论场中流体介质运动时,只考虑介质分子运动的平动特性,而不考虑分子的单独运动。
这样,我们就可以得出静止介质中小振幅声中介质的运动方程为:

式中:u(x,y,z,t)——介质质点的振速分布函数;
p(x,y,z,t)——介质质点压力分布函数;
Po(x,y,z,t)——介质g静态密度分布函数;
其中(x,y,z)为坐标值,t为时间,在介质为均匀时,Po为常数。
上式表征了振速与声压间关系。换句话说,我们也可以用介质中的振速来表征噪声的大小及规律。
根据介质连续性假设,三环减速器表面的振速就是与它相近的邻近介质(空气)的振动速度。这样,在近场中测量噪声值时,我们就可以用三环减速器箱体——Ⅱ子模型表面有振动速度来表示。
在第三章中我们已建立了三环减速器箱体的理论模型,在第四章中我们又计算了各种工况下,Ⅰ子模型对Ⅱ子模的激励X(ω)的大小,这样我们就可以使用SUN工作站上I—DEAS软件中动态分析软件来计算Ⅱ子模型表面的振动速度。
这样,我们就达到了对三环减速器进行振动噪声值预估的目的。
振动速度级:

式中:V——速度均方根值或峰值,单位mm/s;
Vo——参考电平,Vo=5×10-5mm/s
声压级:

式中:P——声压,单位Pa;
Po——2×10-5Pa
声强级:

式中:I——声强;
IO=10-12W/m2
再振动速度级表征振动所产生的噪声的声压级,这两者的关系是:振动速度级若降低若干分贝。因此,若已知振动的表面的振动速度级后,即可明确该振动所产生的噪声的声压极,进而就可以计算出噪声的声强及声功率。
§5-3 三环减速噪声振动速度级预估值计算
在第三章中我们建立并求解了SHQ40三环减速器的理论模型,在第四章我们又通过试验的方法分析求解了SHQ40在四种工况下的激励源的载荷谱,(如图4-11、图4-12、图4-13及图4-14所示,这样我们就可以将载荷加在理论模型上,在SUN工作站上使用I——DEAS软件的系统动态分析模块进行系统响应计算了。
如图6-4所示,我们将载荷沿X向加在SHQ40三环减速器箱体的理论模型的输入轴承座孔处对振动系统进行激励,然后沿Z向计算分析点2点5和点8的振动速度。
在如图4-11和1000rpm-100kgm工况下的载荷谱的激励作用下,SHQ40振动系统测点2、5、8Z向的振动速度的幅值谱函数如图5-1、图5-2、图5-3和图5-6为其相应的时域波形。振动速度预度估值与试验实测值(如表6-10)的对比如表5-1的工况一。
在如图4-12的1000r/m-250kgm工况下的载荷谱的激励作用下,SHQ40振动系统浊点2、5、8Z向的振动速度的幅值谱函数如图5-7、图5-8、图5-9所示。图5-10、图5-11和图5-12为其相应的时域波形。振动速度预估值与试验实测值(如表6-11)的对比见表5-1所示的工况二。
在如图4-13的1000rm-3350kgm工况下的载荷谱的激励作用下,SHQ40振动系统测点2、5、8Z向振动速度的幅值谱函数如图5-13、图5-14和图5-15所录,图5-16、图5-17和图5-18为其相应的时域波形。振动速度的预估值与试验的实测值(如表6-12)对比见表5-1所示的工况三。
在如图4-14的1000rm-400kgm工况下的载荷谱的激励作用下,SHQ40振动系统测点2、5、8Z向的振动速度的幅值函数如图5-19、图5-20和图5-21所录,图5-22、图5-23和图5-24为其相应的时域皮形。振动速度的预估值与试验的实测值(如表6-13)对比见表5-1所示的工况四。
表5-1 SHQ40振动速度级对比表
| 工况 |
测点 |
VrmsE |
LVE |
Vrmso |
LVC |
误差% |
| 一 |
2Z
5Z
8Z |
-
-
7.725 |
-
-
103.78 |
3.46
6.92
7.76 |
86.80
102.82
103.82 |
-
-
0.04 |
| 二 |
2Z
5Z
8Z |
4.255
7.870
8.802 |
88.60
103.94
104.91 |
4.41
8.39
8.81 |
88.91
104.50
104.92 |
0.35
0.54
0.01 |
| 三 |
2Z
5Z
8Z |
4.277
-
9.093 |
88.64
-
105.19 |
4.78
9.08
9.41 |
89.61
105.18
105.49 |
1.09
-
0.29 |
| 四 |
2Z
5Z
8Z |
5.684
9.780
10.257 |
101.11
105.83
106.24 |
5.71
10.28
10.71 |
101.15
106.28
106.62 |
0.04
0.41
0.36 |
表中,Vrmse是振动速度测验实测值的均方根值,如表6-10、表6-11、表6-12和表6-13中数值决定,单位为mm/s;LVE为VrmsE的振速级,由式(5.2)计算,单位dB;VrmsC为振动速度计算预估值,由图5-1~图5-24计算而来,单位为mm/s;LVC为Vrmsc的振速级,由式(5-2)计算,单位dB。
误差由式(5.5)计算:


图5-1
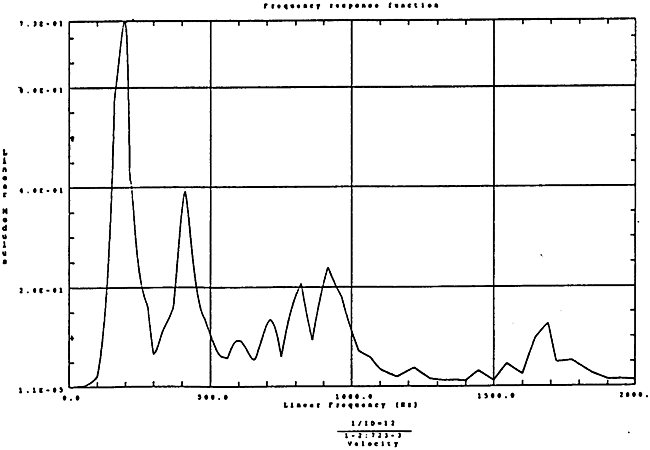
图5-2
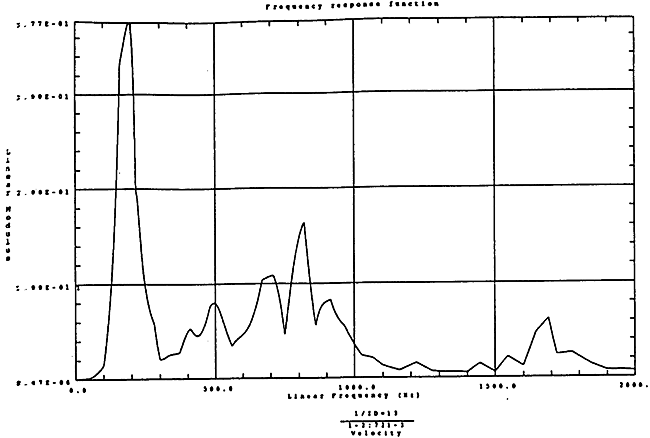
图5-3
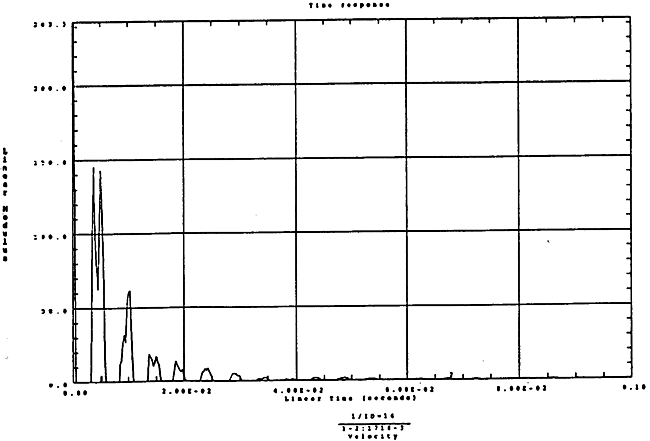
图5-4
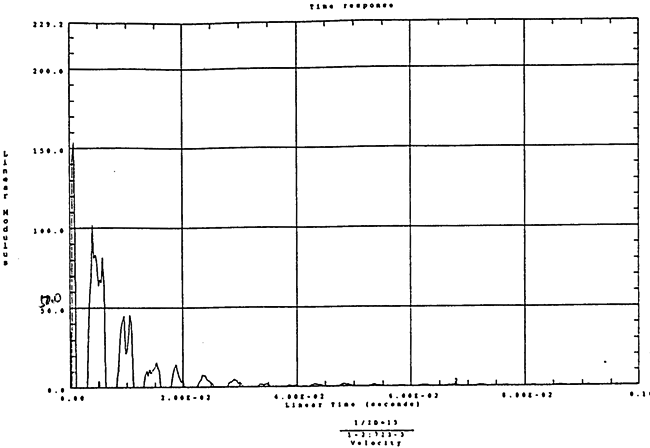
图5-5
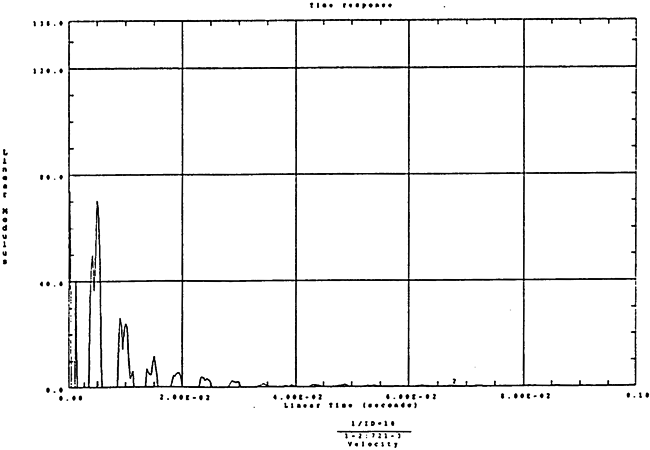
图5-6
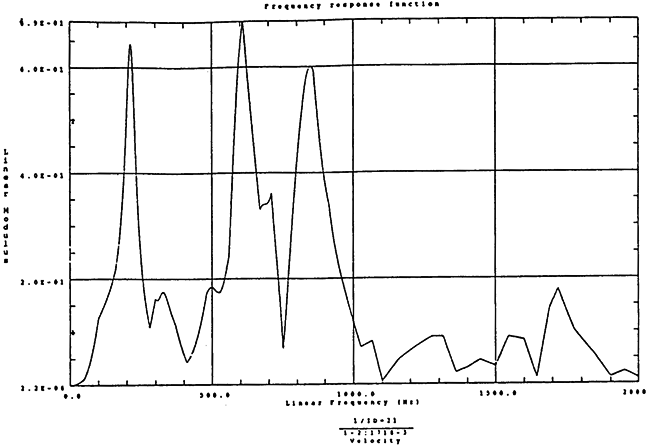
图5-7
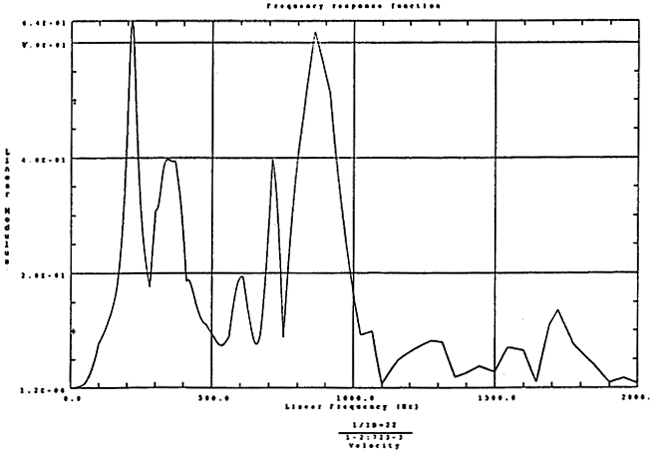
图5-8
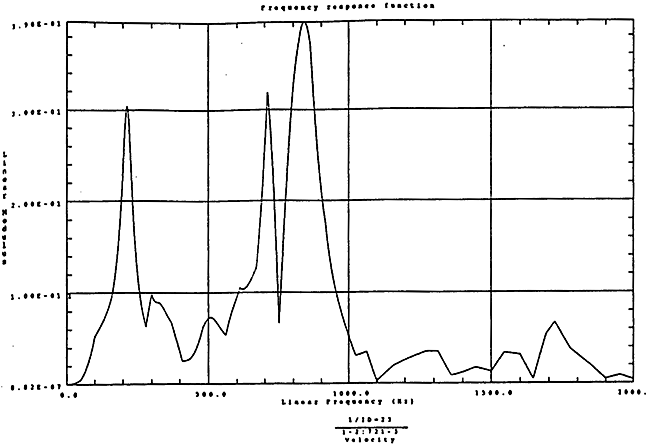
图5-9
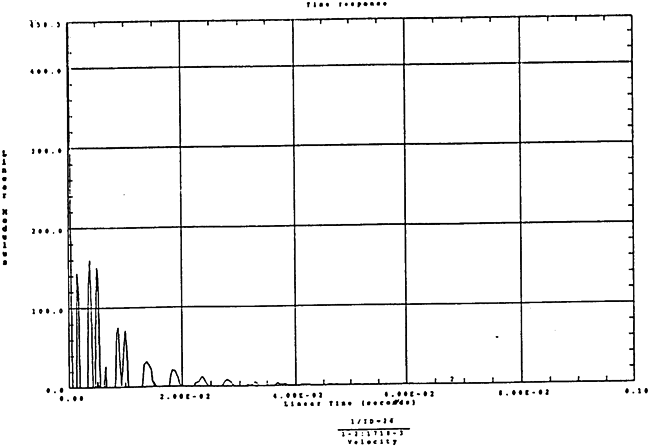
图5-10
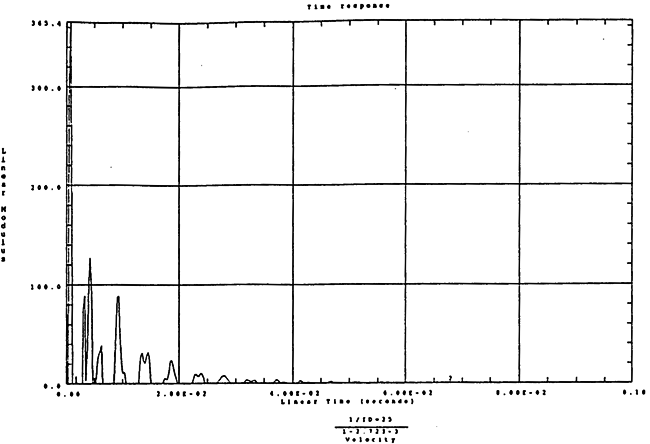
图5-11
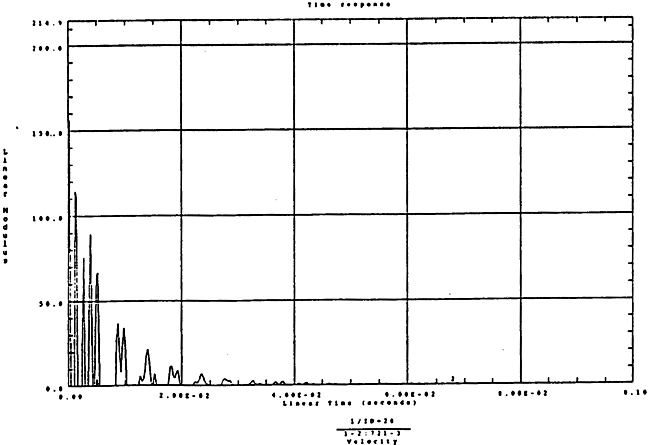
图5-12
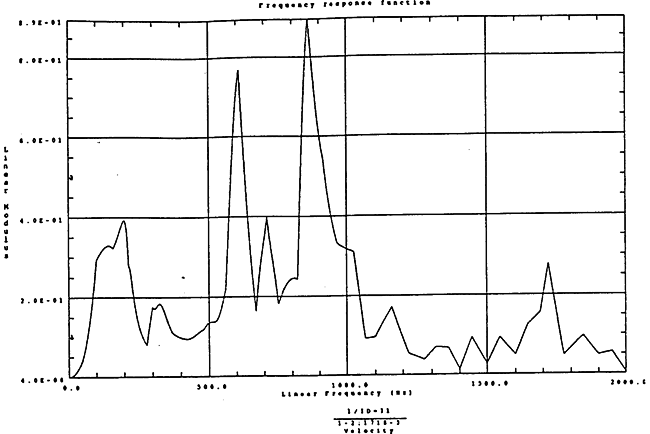
图5-13
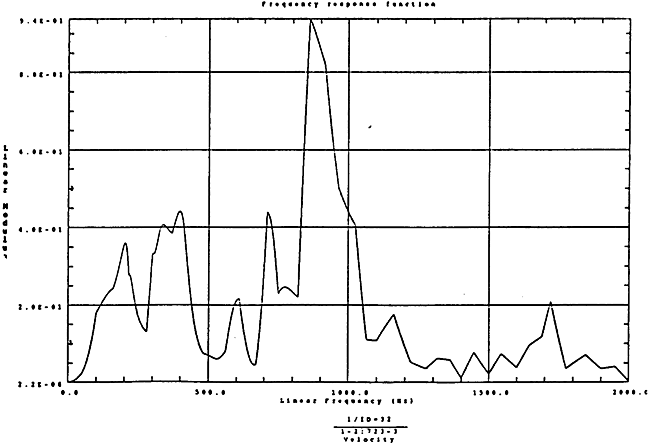
图5-14
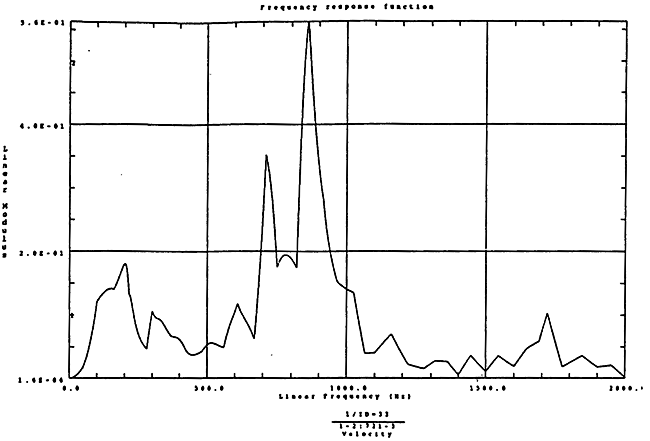
图5-15
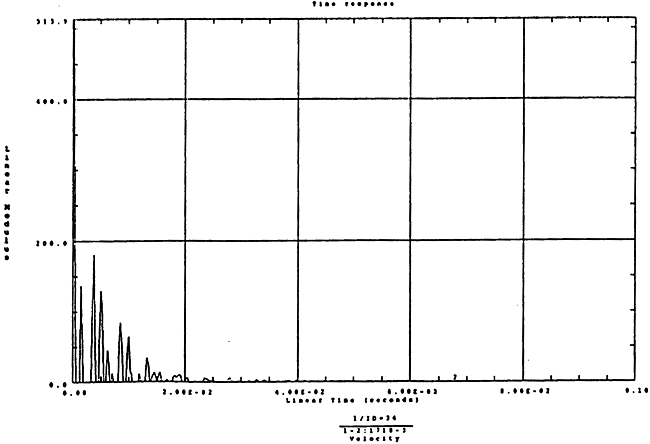
图5-16
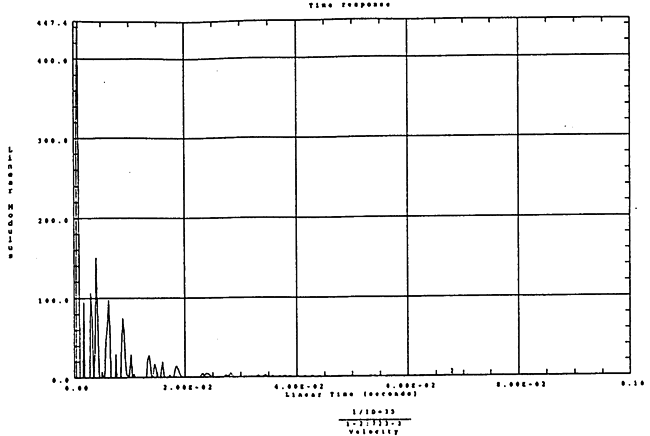
图5-17
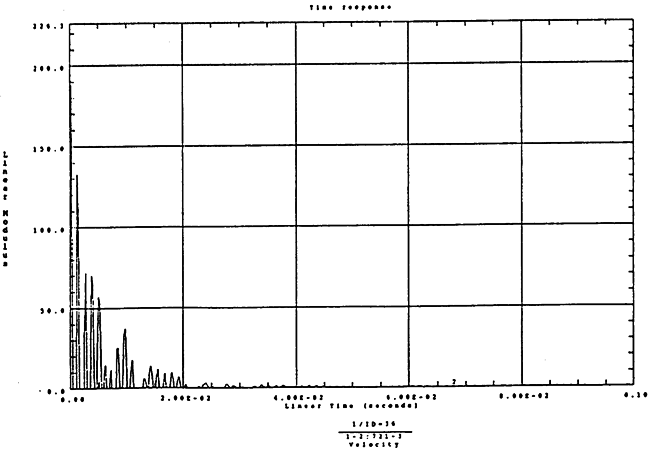
图5-18
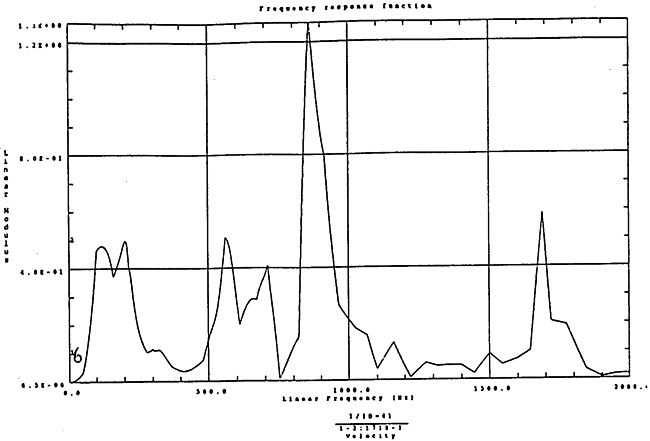
图5-19
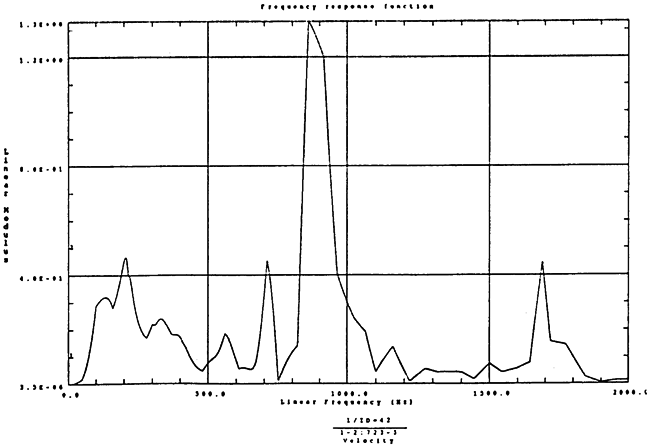
图5-20
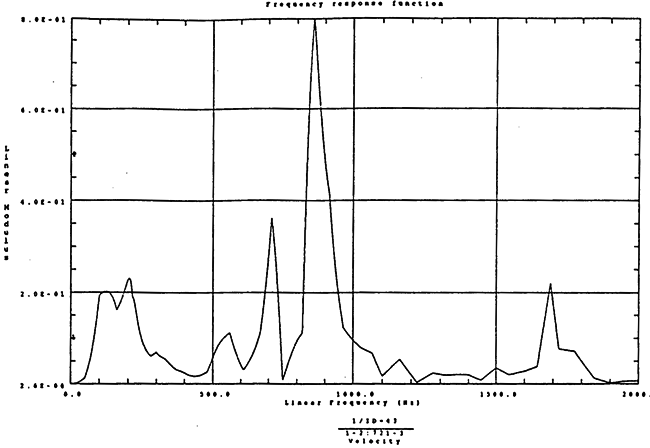
图5-21
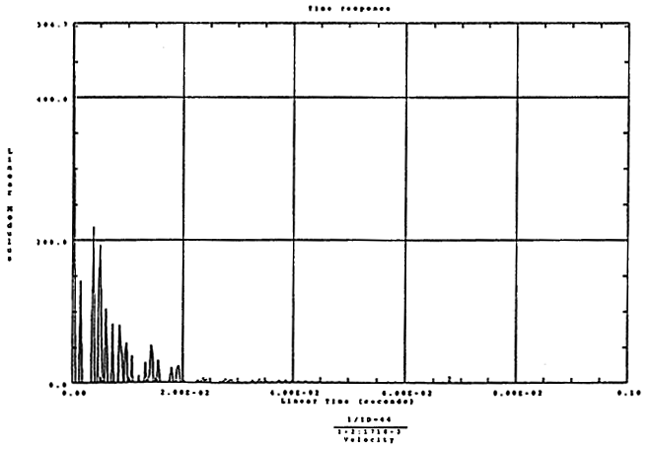
图5-22
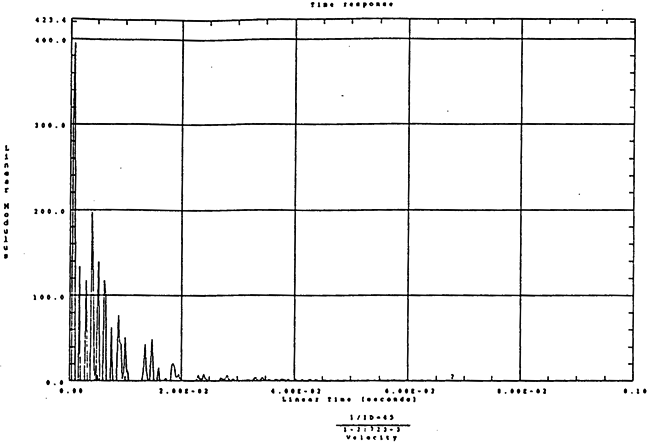
图5-23
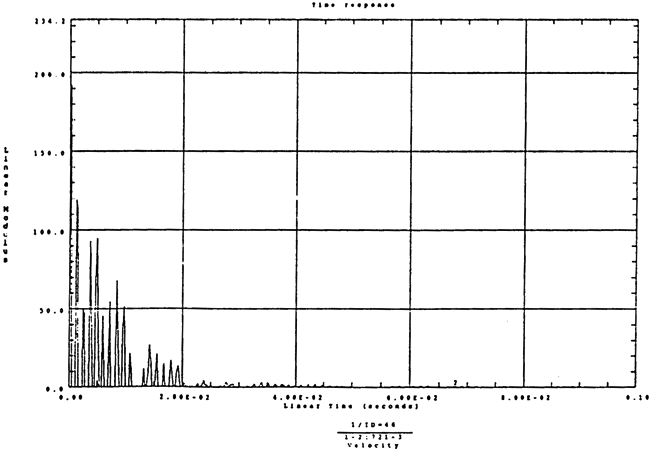
图5-24
从表中可以得出以下规律:
1、输入轴端的振速级大于输出端的振速级;
2、随载荷增加,振速级加大;
3、振速级的预估计算值与试验值误差较小,计算值精度足够,且偏于安全;
4、振速级超标,换句话说SHQ40减速器的振动噪声值超标,标准值最大为90dB。
上一页
下一页
























