第六章 三环减速器振动和噪声试验分析研究
§6-1 引言
以SHQ40型三环减速器分例,我们对三环减速器进行了固有参数测试、振动和噪声级的测试及分析,验证理论建模及噪声预估值计算的可信程度,分析三环减速器的振动机理及振动、噪声分布。
§6-2 振动噪声试验方案
§6-2.1 振动噪声试验方案设计
试验方案设计示意图如图6-0示。
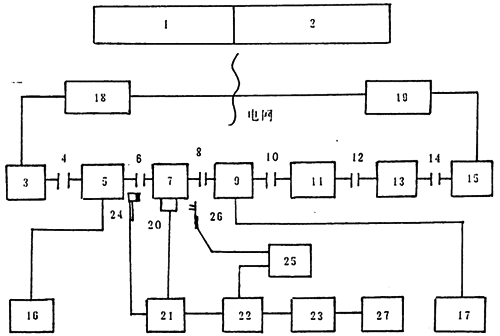
图6-0 试验方案布置
图中:1,2——控制台;
3——100kw直流测功机;
5——联轴器;
4,6,8,10,12,14——输入转速扭矩传感受器;
7,11——SHQ40;
9——输出转速扭矩传感器;
13——汽车变速箱;
15——50kw直流测功机;
16——输入转速扭矩仪;
17——输出转速扭矩仪;
18,19——交直流机组;
20——传感器;
21——放大器2635型;
22——TEAC-5000WB磁带记录仪;
23——CF-355频谱分析仪;
24——脉冲锤;
25——声强仪,Sound Intensity Analyzer Type 4433;
26——声强仪测头,Tho Sound Intensity Probe Type 3520;
27——CX-335绘图仪;
实物如图6-1及图6-2示;

图6-1 电功率流封闭齿轮运转试验台
试验时,通过控制台1,2调节控制系统让交直流机组18发出适当的直流电压使直流测功机3(工作于恒速电动工况)按恒定转速转动,通过联轴器4,6和输入转速扭矩传感器5与试件7输放端(高速端)相联接。试件7输出端通过联轴器8,10,12,14及输出扭矩传感受器9、升速用11、汽车变速箱13而与直流测功机15(工作于恒电流工况)联接,驱使其发出适当电压的直流电,再通过交直流机组19将其逆变成为工频北流电返回电网,完成整个电功率封闭闭链。

图6-2 控制台
输入转速扭矩传感器5得到的输入转速和输入扭矩信号,通过输入扭矩仪16直接数显读出。同样,输出转速扭矩传感器9得到的输出转速和转速扭矩信号,可通过输出扭矩仪17直接数显读出。
试件7上的振动信号与脉冲激励的响应信号通过传感器20取出信号,然后经过放大器21放大后,用磁带记录仪22记录并可采用频谱分析仪23监控并分析,而其上的噪声信号可以通过声强仪25的测头26取出信号后送入22和23中用于分析研究。
§6-2.2 SHQ40试件及测点布置
SHQ40试件如图6-4(a)(b)所示。
其主要特性参数如下:
一、名称:SHW40
二、传动比:i=16;
三、输出扭矩:Mout=4.196KNm;
四、箱体材料:HT20-40
a.抗拉强度:δb=314MPa
b.抗弯强度:δbB=520MPa
c.布氏硬义:HB=187~255;
d.抗压强度:δbc=736MPa
e.弹性模量:E=118~126GPa
f.切变模量:G=44.3GPa
g.泊松比:μ=0.3
h.密度γ=7.0g/cm3

图6-3 SHQ40三环减速器
五、环板材料:45#钢
六、齿轮材料:45#钢
七、齿轮副齿数:
a.内齿轮齿数:51
b.外齿轮齿数:48
八、齿轮齿形:渐开线
九、轴承
a.箱体上:输入轴与支承轴端为深沟球轴承409:
输出端为调心滚子轴承53518
b.环板上:输入轴与支承轴上为E92515。
十、重量:
三环减速器上测点布置如图6-4示。
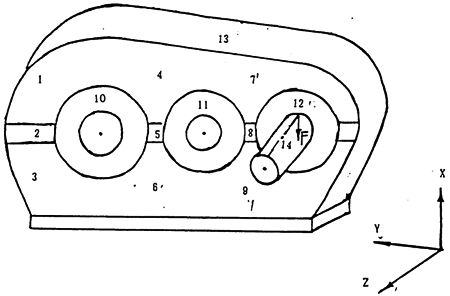
图6-4 SHQ40试件测点
§6-2.3 试验规程
一、跑合试验
1、在200rpm、300rpm、400rpm、500rpm、600rpm、700rpm、800rpm、900rpm及1000rpm转速下用30号机员跑合二十小时;
2、清选SHQ40,然后加双曲线齿轮油;
3、在400rpm、650rpm-50kgm、850rpm-100kgm、1000rpm-150kgm、1000rpm-200kgm、1000rpm-300kgm、1000rpm-400kgm、1000rpm-440kgm工况下跑合二十小时。
4、清选SHQ40然后加双曲线齿轮油,准备试验。
二、空载试验
1、在转速为400rpm工况下,测定并记录试件SHQ40上测点1~12点的振动速度和加速度;
2、在转速为750rpm工况下,测定并记录试件SHQ40上测点1~12点的振动速度和加速度;
3、在转速为1000rpm工况下,测定并记录试件SHQ40上测点1~12点的振动速度和加速度;
三、加载试验
1、在1000rpm-100kgm工况下测定并记录SHQ40上测点1~12的振动速度、加速度及声压和声强;
2、在1000rpm-250kgm工况下测定并记录SHQ40上测点1~12的振动速度、加速度及声压和声强;
3、在1000rpm-350kgm工况下测定并记录SHQ40上测点1~12的振动速度、加速度及声压和声强;
4、在1000rpm-400kgm工况下测定并记录SHQ40上测点1~12的振动速度、加速度及声压和声强;
四、脉冲激励试验
1、固有特性参数测试
敲击测点1~12,在测点13处记录分析;
2、频响函数测试
沿X向敲击试件SHQ40上输入轴上的14点并记录测点12的响应信号,用于分析计算。
§6-3 SHQ40试件振动频率计算
一、转轴频率
由式(2.3)可计算出SHQ40在各工况下转轴频率,如表6-1示,其中输入轴频率为fin,输出轴频率为fout,转速单位转/分(rpm)。
表6-1 转频表
| 输入轴转速(rpm) |
400 |
750 |
1000 |
| 输出轴转速(rpm) |
25 |
46.87 |
62.50 |
| fin(Hz) |
6.67 |
12.50 |
16.66 |
| fout(Hz) |
0.41 |
0.78 |
1.04 |
二、轮齿的啮合频率
由式(2.2)可计算出SHQ40在各种工况下轮齿的啮合频率,见表6-2示。
表6-2 啮频表
| 输入轴转速(rpm) |
400 |
750 |
1000 |
| ft(Hz) |
340 |
637.5 |
850 |
三、轴承频率
由式(2.4)、(2.5)、(2.6)、(2.7)可计算出各轴承在不同工况下的外圈频率for、内圆频率fin滚子元件频率fb及保持架频率fo,见表6-3示
表6-3 轴承频率
| 转速 |
轴承 |
| 409 |
453518 |
92515E |
| 频率 |
| for |
fin |
fb |
fo |
for |
fin |
fb |
fo |
for |
fin |
fb |
fo |
| 400 |
21.6 |
31.7 |
33.0 |
2.7 |
5.2 |
5.2 |
2.8 |
0.2 |
31.2 |
42.2 |
44.6 |
2.8 |
| 750 |
40.5 |
59.5 |
61.9 |
3.9 |
9.8 |
9.8 |
5.3 |
0.3 |
58.4 |
79.1 |
83.7 |
5.3 |
| 1000 |
54 |
79.3 |
82.6 |
9.9 |
13.1 |
7.1 |
7.1 |
0.4 |
77.9 |
105.4 |
111.6 |
7.1 |
四、平面四杆机构产生的激励频率
由式(2.8)、式(2.9)可计算出在各种工况下由平面四杆机构所产生的激励频率如表6-4。
表6-4 平面四杆机构死点冲击激励频率表
| 输入轴转速(rpm) |
400 |
750 |
1000 |
| fN |
6.67 |
12.50 |
16.66 |
| fmx |
13.33 |
25 |
33.33 |
| fmt |
680 |
1275 |
1700 |
五、箱体固有频率
见第三章表3-1。
§6-4 SHQ40固有频率试验
本试验采用脉冲激励法中的锤击法测试SHQ40三环减速器的固有频率,有关脉冲激励法的理论及方法已在第三章中详细论述过了。
脉冲激励信号采样的触发值的大小及方法、位置及其窗函数如图6-5所录。脉冲响应信号所加的窗函数——指数窗如图6-6所示。
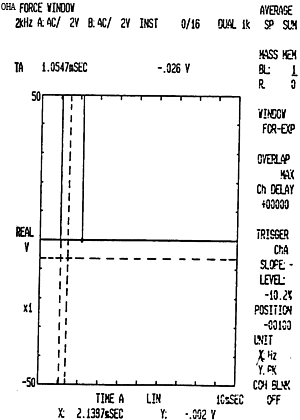
图6-5 脉冲激励信号力窗
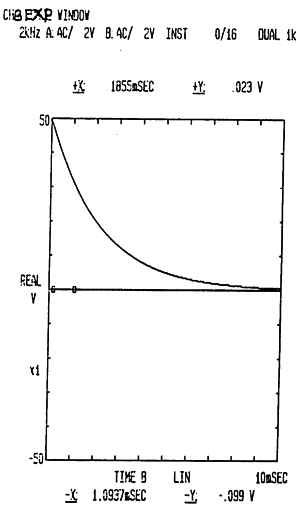
图6-6 脉冲响应信号指数窗
脉冲激励信号及响应信号的时域波形及自功率谱密度函数分别如图6-7和图6-8示。由图中可以看出,脉冲激励信号及其响应信号都较为理想。
在本试验中,通过锤击SHQ40试件上的测点1~12,而在测点13上记录其响应信号,在此我们仅取测点及测点5来讨论。
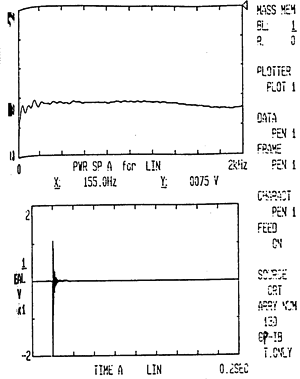
图6-7 脉冲激励信号
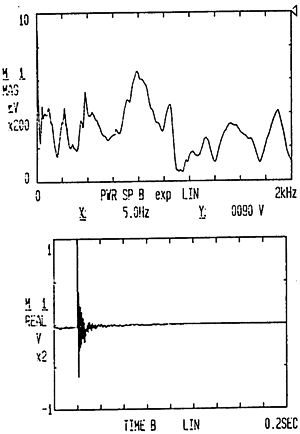
图6-8 脉冲响应信号
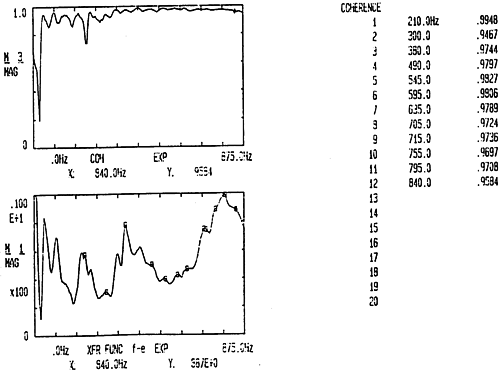
图6-9 13Z-5Z测试
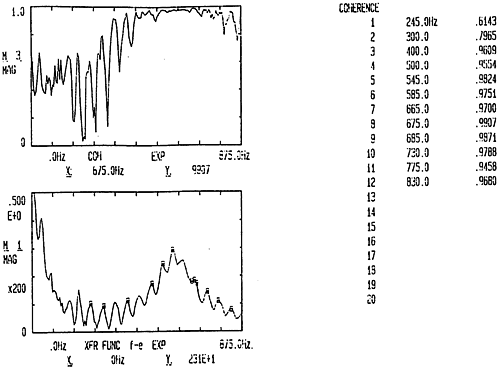
图6-10 13X-5Z测试
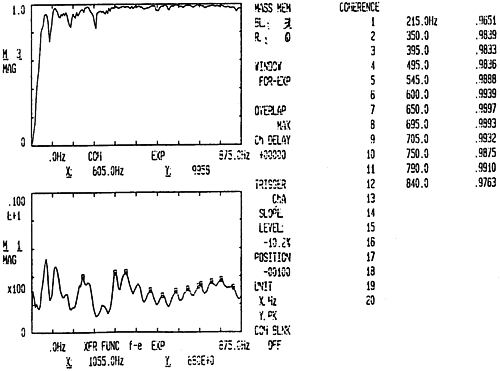
图6-11 13Z-8Z测试
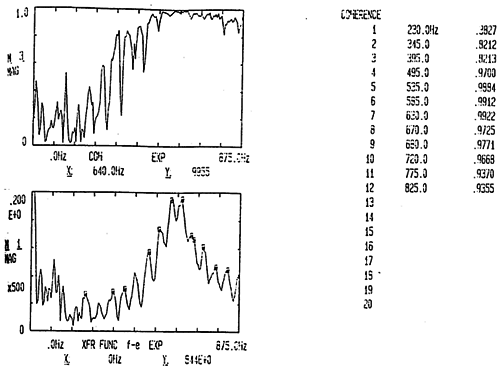
图6-12 13X-8Z测试
图6-9及图6-10分别是锤击测点5Z方向而在测点13Z向和X向采集响应信号经CF-355型频谱分析仪分析后而得出的频响函数及其相干函数以及SHQ40前十二阶模态固有频率值,其与理论建模通过FEM法计算而得的固有频率值对比见表6-5。
图6-11及图6-12分别是锤击测点8Z方向而在测点13Z向和X向采集信号经CF-355型频谱分析仪分析后而得出的频响函数、相干函数以及SHQ40前十二阶模态固有频率值,其与理论建模通过FEM法计算出的固有频率值对比见表6-6示。
从表6-5和表6-6中固有频率的理论建模通过FEM法算出的计算值与脉冲激励阶测出的试验值对比可知,它们前十二阶模态的固有频率值相符性较好,尽管存在一定的误差,但都在允许的范围之内。换句话说,我们建立的理论模型在一定的范围内(本文只研究了前十二阶模态950HZ以内的范围)是可以替代实际的结构用于分析、研究及计算。
造成固有频率计算值与试验值之间误码率差的因素有以下几个方面:
1、由实际结构进行一定简化而建立理论模型而带来的误差;
2、FEM法本身所带来的近似误差;
3、加在理论模型上的约束和载荷与实际结构的工况之间误差;
下面我们列出SHQ40振动系统850HZ-2KHZ间各阶模态固有频率的试验值。如图6-13示。图中左上部为相干函数,左下部图为频响函数图,而右半图部分为十三阶到三十一阶固有频率值及其相干值。
表6-5 固有频率计算值与试验对比表
| 序号 |
计算值HZ |
13Z-5Z值Hz |
误差% |
13X-5Z值Hz |
误差% |
1
2
3
4
5
6
7
8
9
10
11
12 |
215.0
322.9
409.2
501.0
537.5
577.7
670.4
673.1
683.1
754.8
765.7
851.7 |
210.0
300.0
380.0
490.0
545.0
595.0
635.0
705.0
715.0
755.0
795.0
840.0 |
2.0
7.0
7.0
2.0
1.0
2.0
5.0
4.0
4.0
0.0
3
1 |
245.0
300.0
400.0
500.0
545.0
585.0
665.0
625.0
685.0
730.0
775.0
830.0 |
13.0
2.0
7.0
0.0
1.0
1.0
0.0
0.0
0.0
3.0
1.0
2.0 |
表6-6 固有频率计算值与试验对比表
| 序号 |
计算值HZ |
13Z-5Z值Hz |
误差% |
13X-5Z值Hz |
误差% |
1
2
3
4
5
6
7
8
9
10
11
12 |
215.0
322.9
409.2
501.0
537.5
577.7
670.4
673.1
683.1
754.8
765.7
851.7 |
215.0
350.0
395.0
495.0
545.0
600.0
650.0
695.0
705.0
750.0
790.0
840.0 |
0.0
8.0
3.0
1.0
1.0
3.0
3.0
3.0
3.0
0.0
3.0
1.0 |
230.0
345.0
395.0
495.0
535.0
585.0
630.0
670.0
680.0
720.0
775.0
825.0 |
6.0
6.0
3.0
1.0
0.0
1.0
6.0
0.0
0.0
4.0
1.0
3.0 |
阶固有频率值及其相干值。
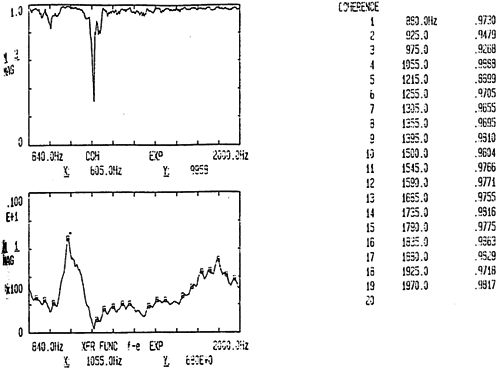
图6-13 固有频率值及相干值
上一页
下一页














