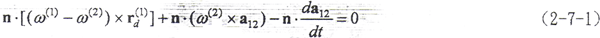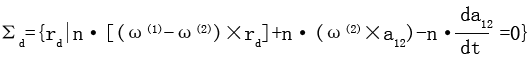第二章 弹性共轭曲面原理的研究
2.1 导言
弹性共轭曲面原理的研究是为了适应现代机械工业发展的需要,解决成对弹性体曲面的几何图形及其运动间的关系的问题。在机械制造和机械设计中,都存在共轭曲面问题,它们对加工质量和传动性能都有非常大的影响。在有弹性变形时,共轭曲面的几何图形及其运动间的关系将与由刚性条件下得出的结果不同,从而不能满足原来所设想的要求。尤其在刚性较差的零件加工和大柔性的传动中,弹性变形对共轭关系的影响就更为重要。如在齿轮传动方面,以往的轮齿修形的研究主要是针对多齿啮合的啮合齿对数变化的过渡状态的。而在非多齿啮合过渡状态,由于变形的作用,共轭条件也会遭到破坏,尤其在大齿面和大柔性的传动中,弹性变形的影响是不能忽略的。因此,这些修形的研究由于缺乏具有普遍意义的理论的指导,都存在一定的片面性。随着机械加工向高精度、高效率的发展和机械传动向大载荷、高性能的发展,迫切需要新的弹性共轭曲面理论作为指导,解决机械设计和机械制造中出现的弹性共轭曲面问题。
本文提出了弹性共轭曲面的基本理论,建立弹性共轭曲面运动基本方程,研究弹性共轭曲面的一般求解方法,为进一步深入全面地研究弹性共轭曲面问题奠定理论基础。
2.2 弹性共轭曲面研究的前提假设
弹性共轭曲面原理的研究是一个复杂的问题,为了突出主要问题,因而忽略一些因素的影响,首先作出一些前提假设,而且本文只研究线接触弹性共轭曲面问题。
1.所研究的变形是在弹性变形范围,受力变形在作用力消除后完全恢复,即变形曲面的完全弹性体概念;
2.忽略接触曲面间的相互摩擦作用,即忽略曲面上的切向力的作用;
3.不考虑热变形;
4.弹性变形相对于曲面的相对运动无滞后。
2.3 弹性共轭曲面定义
弹性共轭曲面的定义是:两弹性体在外力作用下产生弹性变形后,彼此既保持连续相切接触,又不互相干涉,并且按给定运动规律运动的一对弹性变形恢复后的曲面。
一对弹性体曲面在外力作用下的运动规律与在弹性变形恢复状态下几何图形间关系的研究就是弹性共轭曲面研究的内容。弹性共轭曲面是在受力变形下仍保持共轭运动规律的,它们在相互接触的运动过程中几何形状是不断变化的,是动态的过程,我们最终需要求解的弹性共轭曲面不是这一系列的动态的几何图形,而是利用这些动态的几何图形和它们的相对运动要求来求解在不受力变形状态下的曲面几何图形及其运动关系。
根据上述弹性共轭曲面概念可知,一对弹性共轭曲面在外力作用下相互接触产生弹性变形,接触参考点处的两曲面的速度矢量沿该点的公法线的投影应相等,有
v(1)·n=v(2)·n
即
v(12)·n=0
这就是弹性共轭曲面在相对运动时所应满足的要求。
2.4 弹性共轭曲面的运动分析
2.4.1 坐标系(如图2-1所示)
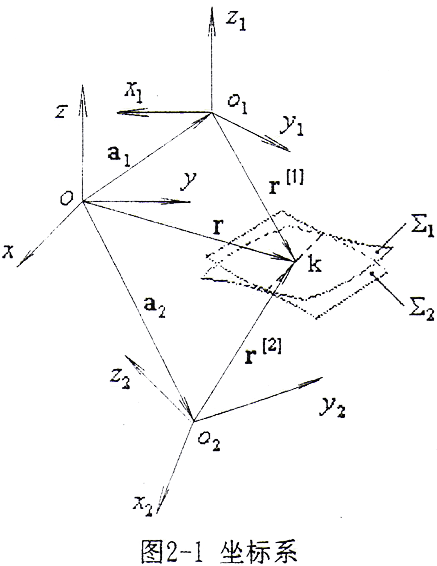
坐标系S1(o1,x1,y1,z1):与曲面Σ1固连的动坐标系;
坐标系S2(o2,x2,y2,z2):与曲面Σ2固连的动坐标系;
坐标系S(o,x,y,z):静坐标系;
设K点为两曲面受力变形后的接触参考点,a1、a2为静坐标系S原点到两动坐标系S1和S2原点的径矢;r(1)、r(2)为Σ1、Σ2上K点在S1、S2坐标系的径矢;r为K点在S坐标系的径矢。
2.4.2 弹性体接触参考点的运动分析
由图2-1知
r=r(1)+a1
所以有
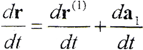
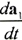 表示动坐标系S1的原点o1相对于静坐标系S的运动速度矢量。
表示动坐标系S1的原点o1相对于静坐标系S的运动速度矢量。
由于 r(1)=x1i1+y1j1+z1k1
所以
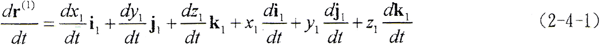
若为刚性曲面,则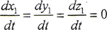 ,由于现在所研究的曲面为弹性曲面,接触参考点在S1坐标系的径矢将随弹性变形而发生变化,因此,
,由于现在所研究的曲面为弹性曲面,接触参考点在S1坐标系的径矢将随弹性变形而发生变化,因此,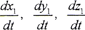 不恒等于零,令
不恒等于零,令
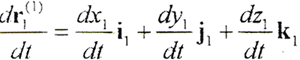
显然它是Σ1上接触参考点在S1坐标系的径矢对时间的变化率,即接触参考点相对于S1坐标系的速度矢量。
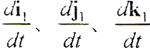 为S1坐标分量的单位矢量对时间的微分[2]。
为S1坐标分量的单位矢量对时间的微分[2]。
由i1⊥j1⊥k1
i1·j1=j1·k1=k1·i1=0有
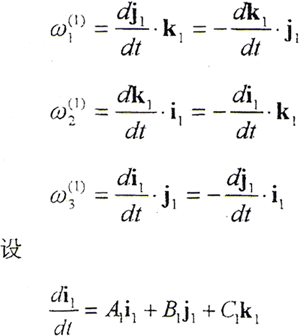
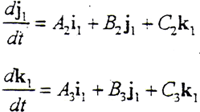
以i1、j1、k1分别点乘以上三式的两边,有
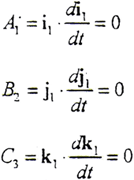
同理可得
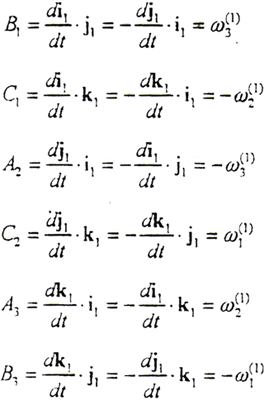
所以有

令 ω(1)=ω1(1)i1+ω2(1)j1+ω3(1)k1
而 r(1)=x1i1+y1j1+z1k1
则有
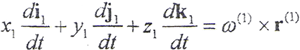
所以

式中ω(1)为S1坐标系的角速度矢量。
2.4.3 弹性体相对运动分析
由前推导知,Σ1上K点的相对于S坐标的速度

式中
r(2)=x2i2+y2j2+z2k2
ω(2)=ω1(2)i2+ω2(2)j2+ω3(2)k2
ω(2)为S2坐标系的角速度。
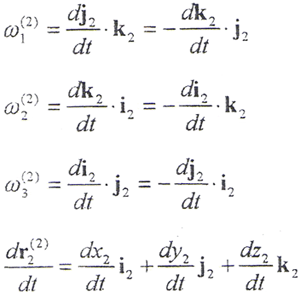
 包含坐标系S1、S2原点的运动速度和由变形使原点位置产生变化的速度。
包含坐标系S1、S2原点的运动速度和由变形使原点位置产生变化的速度。
所以,Σ1、Σ2在K点的相对速度
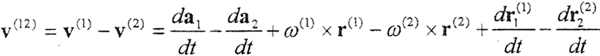
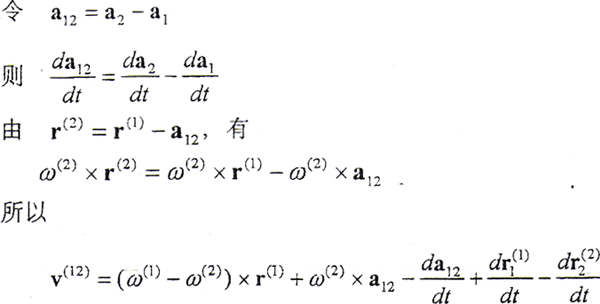
a12为坐标系S1原点至坐标系S2原点的矢量,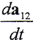 为坐标系S1、S2原点的相对运动速度矢量,它可包含两共轭曲面支承件的弹性变形速度,
为坐标系S1、S2原点的相对运动速度矢量,它可包含两共轭曲面支承件的弹性变形速度,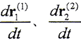 分别为曲面Σ1、Σ2上接触参考点相对于坐标系S1、S2的弹性变形速度矢量。
分别为曲面Σ1、Σ2上接触参考点相对于坐标系S1、S2的弹性变形速度矢量。
2.5 弹性共轭曲面运动基本方程
根据弹性共轭曲面在相对运动时所应满足的条件
n·v(12)=0
即有
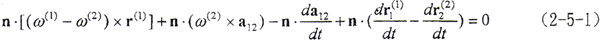
(2-5-1)式就是弹性共轭曲面运动基本方程。
若为刚性曲面,上式中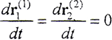 ,则可由(2-5-1)式得出传统的刚性共轭曲面运动基本方程。由此可知,刚性共轭曲面只是弹性共轭曲面的特殊情况。
,则可由(2-5-1)式得出传统的刚性共轭曲面运动基本方程。由此可知,刚性共轭曲面只是弹性共轭曲面的特殊情况。
(2-5-1)式中有三个运动矢量ω(1)、ω(2)、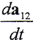 ,不同的共轭运动形式,其三个运动矢量方向都是确定的。在机械加工中,根据不同情况有不同的运动自由度,均可用以上三个运动矢量确定;在啮合传动中,最一般情况为相错轴传动,在定轴传动中,如果不考虑轴系的变形,则
,不同的共轭运动形式,其三个运动矢量方向都是确定的。在机械加工中,根据不同情况有不同的运动自由度,均可用以上三个运动矢量确定;在啮合传动中,最一般情况为相错轴传动,在定轴传动中,如果不考虑轴系的变形,则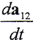 =0,(2-5-1)式成为
=0,(2-5-1)式成为
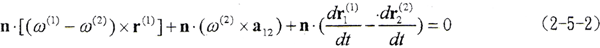
2.6 变形对接触参考点法线方向的改变
由于变形的作用,接触参考点的法线方向将发生一定的变化,以下分析在xoy平面内接触参考点法线方向的改变量。
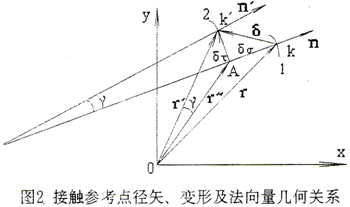
如图2所示,变形前,曲面在位置1;变形后,曲面在位置2。变形前后接触参考点为k、k′。变形前的接触参考点径矢及法线向量为r、n;变形后的接触参考点径矢及法线向量为r′、n′。设变形为δ,其切向分量和法向分量分别为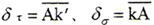 。变形前后的法线向量夹角为γ。r″为只产生法向变形后的接触参考点径矢。在小变形条件下,可认为只产生切向变形后的接触参考点径矢与法线向量的夹角不变,即r″与n的夹角等于r′与n′的夹角。由几何关系有
。变形前后的法线向量夹角为γ。r″为只产生法向变形后的接触参考点径矢。在小变形条件下,可认为只产生切向变形后的接触参考点径矢与法线向量的夹角不变,即r″与n的夹角等于r′与n′的夹角。由几何关系有

式中 ∠k′A0=3π/2-∠kA0
设r、n之间的夹角为ε,则有
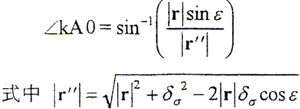
通常情况下,变形量相对于曲面参考点径矢的大小为微小量,其切向分量更小,主要由挠曲变形引起。由(2-6-1)式知,γ值非常小。一般情况下,可忽略这一法线方向的改变,认为变形后的接触参考点法线方向不变,以便于求解。
2.7 弹性共轭曲面的求解
2.7.1 求解思路
弹性共轭运动的过程,实质上是两动态变形曲面互为包络的过程,对变形过程中的曲面的描述是非常困难的,而我们所关心的是变形恢复状态的曲面如何保证在一定的载荷作用下满足变形条件的共轭运动规律,因此,可不去描述这个动态变曲面的全过程。
由(2-5-1)式知,它是r(1)、r(2)需满足的微分方程。Σ1、Σ2在接触的最初阶段,接触参考点在接触力作用下,随着Σ1、Σ2的相对运动,变形逐渐增大,在此阶段,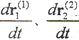 不为零。当接触参考点变形达到最大时,该瞬间变形结束,回弹尚未开始,显然,此瞬时
不为零。当接触参考点变形达到最大时,该瞬间变形结束,回弹尚未开始,显然,此瞬时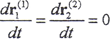 ,这时的接触参考点为决定两曲面运动关系的点,受力达到平衡,我们称这样的接触参考点为变形最大点。将这样的点之径矢记为rd(1)、rd(2),(2-5-1)式就成为
,这时的接触参考点为决定两曲面运动关系的点,受力达到平衡,我们称这样的接触参考点为变形最大点。将这样的点之径矢记为rd(1)、rd(2),(2-5-1)式就成为
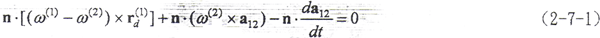
即变形最大点满足条件(2-7-1)式。
与变形最大点相邻的点,变形已经发生,但未达到最大,即使由于变形的关系已接触,但这样的点并不对两曲面的运动起决定作用。当运动继续,相邻点成为变形最大点,原来的变形最大点则处于变形回弹状态。整个连续的曲面之运动就是由无穷多个这样的变形最大点所决定的,我们称这无穷多个变形最大点的动坐标集合为变形基本共轭曲面,简称为变形基本曲面。
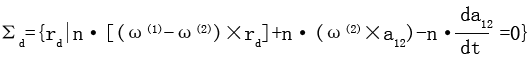
变形基本曲面为共轭运动过程中逐渐形成的,是由变形最大点所构成的假想曲面,它是求解弹性共轭曲面的过渡曲面。变形基本曲面在弹性变形恢复状态所形成的曲面即为弹性共轭曲面。变形基本曲面及其运动关系确定后,则可根据不同的求解要求,求解弹性共轭曲面或求解运动规律。
由以上分析可以看出,弹性共轭曲面的求解,一个重要的问题是接触参考点最大变形的求解。
2.7.2 变形的求解
弹性体的变形可认为是挠曲变形与接触变形的迭加,设所求解的弹性共轭曲面边界及作用在曲面上的作用力为已知,则变形即可求出。随着数学力学的发展,变形的求解也日益精确[26][27][33][35][43][46~50][54~62]。有限元、边界元方法成为求解变形的有力工具。本文不详细讨论变形的求解方法。
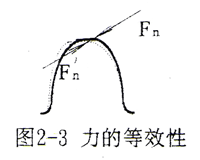
如图2-3所示,变形的恢复可看成在受力变形状态下加上一个与原作用力大小相等、方向相反的作用力。由于变形的微小性,可认为Fn与Fn′的变形效应相同,即Fn′作用下rd(i)的变形恢复量等于Fn作用下产生的变形量,也就是说变形恢复量可由在变形基本曲面上作用相同的力的变形量的计算来确定。
2.7.3 弹性共轭曲面的求解方法
当已知变形基本曲面和在特定载荷下的变形,则可求解弹性共轭曲面。
r(i)=rd(i)+δ(i)·n0(i) (i=1,2) (2-7-2)
式中
r(i)——参考点弹性共轭曲面径矢
rd(i)——参考点变形基本曲面径矢
δ(i)——参考点最大法向变形量
n0(i)——参考点单位法向矢量
弹性共轭曲面Σi即为所有离散点r(i)的集合。
Σi={r(i)|r(i)=rd(i)+δ(i)·n0(i)} (i=1,2)
上一页
下一页


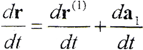
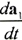 表示动坐标系S1的原点o1相对于静坐标系S的运动速度矢量。
表示动坐标系S1的原点o1相对于静坐标系S的运动速度矢量。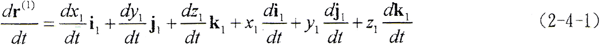
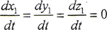 ,由于现在所研究的曲面为弹性曲面,接触参考点在S1坐标系的径矢将随弹性变形而发生变化,因此,
,由于现在所研究的曲面为弹性曲面,接触参考点在S1坐标系的径矢将随弹性变形而发生变化,因此,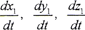 不恒等于零,令
不恒等于零,令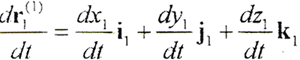
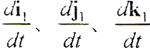 为S1坐标分量的单位矢量对时间的微分[2]。
为S1坐标分量的单位矢量对时间的微分[2]。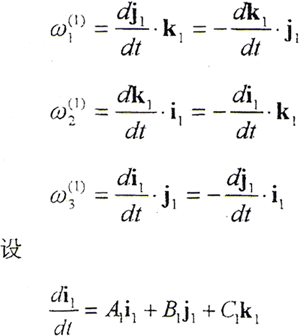
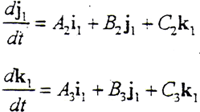
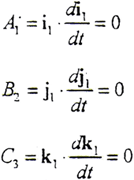
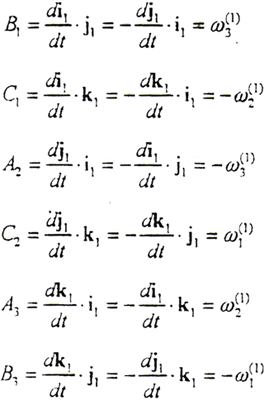

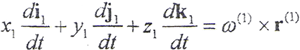


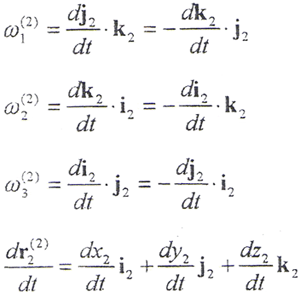
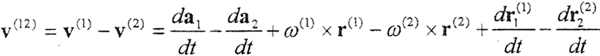
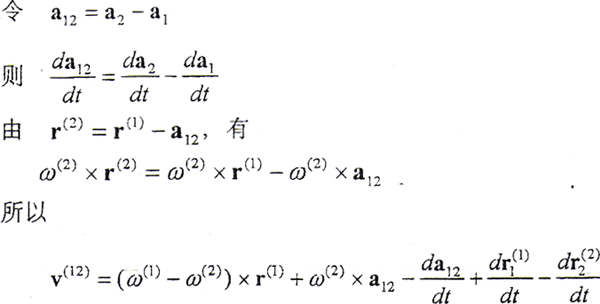
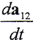 为坐标系S1、S2原点的相对运动速度矢量,它可包含两共轭曲面支承件的弹性变形速度,
为坐标系S1、S2原点的相对运动速度矢量,它可包含两共轭曲面支承件的弹性变形速度,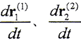 分别为曲面Σ1、Σ2上接触参考点相对于坐标系S1、S2的弹性变形速度矢量。
分别为曲面Σ1、Σ2上接触参考点相对于坐标系S1、S2的弹性变形速度矢量。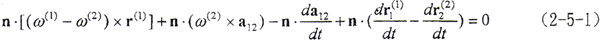
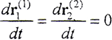 ,则可由(2-5-1)式得出传统的刚性共轭曲面运动基本方程。由此可知,刚性共轭曲面只是弹性共轭曲面的特殊情况。
,则可由(2-5-1)式得出传统的刚性共轭曲面运动基本方程。由此可知,刚性共轭曲面只是弹性共轭曲面的特殊情况。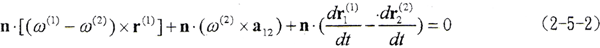

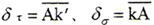 。变形前后的法线向量夹角为γ。r″为只产生法向变形后的接触参考点径矢。在小变形条件下,可认为只产生切向变形后的接触参考点径矢与法线向量的夹角不变,即r″与n的夹角等于r′与n′的夹角。由几何关系有
。变形前后的法线向量夹角为γ。r″为只产生法向变形后的接触参考点径矢。在小变形条件下,可认为只产生切向变形后的接触参考点径矢与法线向量的夹角不变,即r″与n的夹角等于r′与n′的夹角。由几何关系有
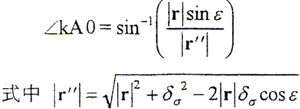
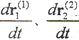 不为零。当接触参考点变形达到最大时,该瞬间变形结束,回弹尚未开始,显然,此瞬时
不为零。当接触参考点变形达到最大时,该瞬间变形结束,回弹尚未开始,显然,此瞬时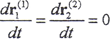 ,这时的接触参考点为决定两曲面运动关系的点,受力达到平衡,我们称这样的接触参考点为变形最大点。将这样的点之径矢记为rd(1)、rd(2),(2-5-1)式就成为
,这时的接触参考点为决定两曲面运动关系的点,受力达到平衡,我们称这样的接触参考点为变形最大点。将这样的点之径矢记为rd(1)、rd(2),(2-5-1)式就成为