第三章 弹性共轭曲面原理的应用研究
3.1 弹性共轭曲面原理的基本问题
由第二章可知,解决弹性共轭曲面,涉及到变形基本曲面Σ1d和Σ2d、啮合轨迹图形Σc、弹性共轭曲面Σ1和Σ2、运动参数V1和V2、曲面的变形dr1(1)和dr2(2),而变形又与Σ1d、Σ2d及作用力有关,这是一个非常复杂的多因素问题,尤其当运动的自由度较大时,问题变得更为复杂。就变形基本曲面Σ1d和Σ2d、啮合轨迹图形Σc、运动参数V1和V2这五个因素而言,存在着如第一章所论述的五类基本问题。由于弹性共轭曲面问题还包含弹性共轭曲面Σ1、Σ2和曲面变形的因素,因此,需求解的内容更为丰富。本文只讨论已知变形基本曲面Σ1d及外力,求给定运动规律下的两弹性共轭曲面,此类问题主要解决啮合传动问题。
3.2 平面啮合传动弹性共轭曲面的求解
定轴平面啮合传动坐标系如图3-1所示。
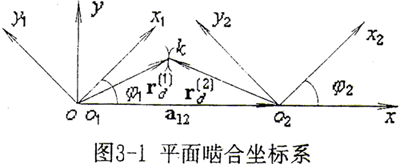
3.2.1 变形基本曲面
在定轴平面啮合中,不考虑轴系的变形,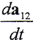 =0,由(2-7-1)式得
=0,由(2-7-1)式得
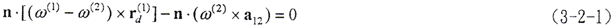
若在变形状态下Σ1d为已知,则可求得与之共轭的变形基本曲面Σ2d。若将(3-2-1)式表示为
f(u,φ1)=0
式中 u——曲面参变量,φ1——Σ1d的转角,则有

式中 M21——S1、S2坐标系转换矩阵
3.2.2 最大变形是关于载荷大小和作用位置的函数
δ(p,u)=δp(p,u)+δb(p,u) (3-2-3)
式中 p——载荷参变量
δ(p,u)——总变形矢量
δp(p,u)——接触变形矢量
δb(p,u)——挠曲变形矢量
通常所求得的变形为数值解。
3.2.3 求解弹性共轭曲面
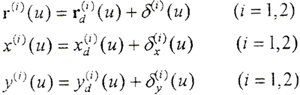
3.2.4 渐开线直齿圆柱标准齿轮传动弹性共轭曲面的求解
1.变形基本曲面
坐标系如图3-1所示。设已知齿轮1的变形基本曲面为渐开线曲面,其端面上的齿面线方程为
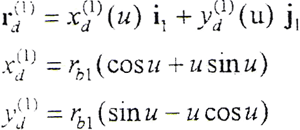
式中 u——曲面参变量
rb1——齿轮1渐开线基圆半径
则
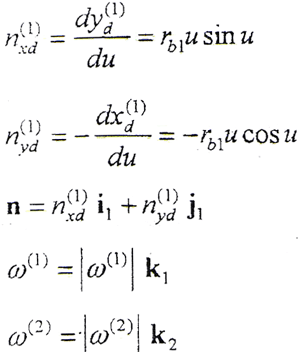
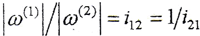
a12=a12i
将rd(1)、ω(1)、ω(2)、a12代入(3-2-1)式,有

化简后得
cos(u-φ1)=rb1/r1=cosα
α为齿轮的分度圆压力角,所以
α=u-φ1
由(3-2-2)式,得
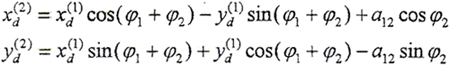
代入并化简得:
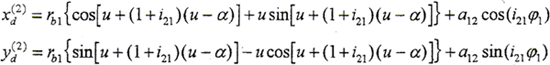
显然Σ2d齿廓曲线也是一渐开线,其基圆半径与i21有关,渐开线起点不在x2轴线上。
2.变形的求解
对于直齿圆柱齿轮变形的求解,已有许多研究[33][46][49][50][54~56][60~62]。文献[49]较好地解决了挠曲变形的问题,提出的变形计算的拟合公式简捷、精度高;文献[46]对接触变形问题根据经典的赫兹公式,推导出直齿圆柱齿轮的接触变形计算公式,计算简便,精度高,本节拟采用上述两公式进行变形计算。
挠曲变形:

其中A、B、C按以下三式计算
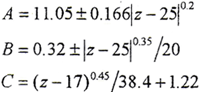
当z<25时取“+”号;当z≥25时取“-”号。
(3-2-4)式中
E——材料弹性模量(kg/mm2)
Pn——作用在齿面上的法向总载荷(kg)
b——齿宽(mm)
z——齿数,z取17~∞,当z>135时,按z=135计算
xr——径向变位系数,xr取值-0.2~1.0
λ——加载点位置系数,λ=(ra-rk)/m,ra为齿顶圆半径,rk为加载点半径,m为齿轮模数
δb——轮齿加载点法向挠曲变形量
(3-2-4)式适合于齿轮材料泊轮比为0.3,无根切无齿顶变尖的直齿圆柱齿轮的挠曲变形的计算。刀具齿条齿形角α=20°,齿顶高系数ha*=1,顶隙系数c*=0.25,刀尖圆角半径r0允许在0.25m~0.4m范围变化。
接触变形:
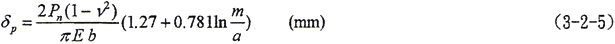
式中
Pn——作用在齿面上的法向总载荷(kg)
E——材料弹性模量(kg/mm2)
v——材料泊松比
b——齿宽(mm)
m——齿轮模数(mm)
a——赫兹接触宽度的一半(mm)
δp——轮齿加载点接触变形量
对于柱体的接触变形,文献[112][113]介绍了赫兹接触半宽度的计算公式
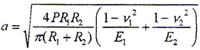
式中
P——单位接触长度上的载荷(kg/mm)
R1、R2——两接触体在接触点的曲率半径(mm)
v1、v2——材料的泊松比
E1、E2——材料的弹性模量(kg/mm2)
当两接触体材料相同时
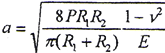
计算变形所需几何尺寸的确定:
模数m,齿数z1、z2,压力角α,变位系数xr1=0、xr2=0,齿宽b,齿顶高系ha*,顶隙系数c*,齿顶圆半径ra1=mz1/2+mha*,齿根圆半径rf1=mz1/2-m(ha*+c*),齿轮1加载点半径r1k变化范围设为 ,曲率半径为
,曲率半径为
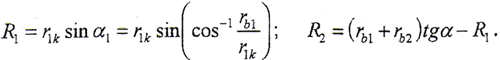
法向作用力:
设已知作用在齿轮1上的转矩为M,则无论接触点在何处,有
Pn=M/rb1
由变形基本曲面的求解得,Σ1d、Σ2d为基圆半径分别为rb1、rb2的渐开线曲面;将以上各已知参数代入(3-2-4)及(3-2-5)式,在r1k取值范围内以一定间隔取若干值分别计算变形,得到两齿面以r1k为参数的变形量离散值,为了求解以u为参变量的弹性共轭曲面,需将其换算为以u为参数的变形量,由r1k与u的关系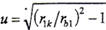 ,即可得到以u为参变量的变形量离散值δ(1)(u)=δp(1)(u)+δb(1)(u)、δ(2)(u)=δp(2)(u)+δb(2)(u)
,即可得到以u为参变量的变形量离散值δ(1)(u)=δp(1)(u)+δb(1)(u)、δ(2)(u)=δp(2)(u)+δb(2)(u)
变形基本曲面单位法向量的分量为
n(1)xd0=sinu,n(1)yd0=-cosu。
3.弹性共轭曲面求解
齿轮1的弹性共轭曲面为
x(1)(u)=xd(1)(u)+δ(1)(u)sinu
y(1)(u)=yd(1)(u)-δ(1)(u)cosu
同理可求得
x(2)(u)=xd(2)(u)+δ(2)(u)sinu
y(2)(u)=yd(2)(u)-δ(2)(u)cosu
下面以m=3mm,z1=29,z2=50,α=20°,ha*=1,c*=0.25,b=30mm,xr1=xr2=0为例求解弹性共轭曲面,设v=0.3,E=2.1×104kg/mm2,M=500.0Nm。
本例弹性共轭曲面计算结果如表3-1所给。为计算方便,设齿面2渐开线起点在x2上。
表3-1 变形基本曲面坐标及弹性共轭曲面坐标
(m=3mm,z1=29,z2=50,α=20°,ha*=1,c*=0.25,b=30mm,xr1=xr2=0,v=0.3,E=2.1×104kg/mm2,M=50.0kgm)
| u1 |
xd(1) |
x(1) |
yd(1) |
y(1) |
u1 |
xd(1) |
x(1) |
yd(1) |
y(1) |
| 0.059942 |
40.9500 |
40.9514 |
0.0029 |
-0.0200 |
0.238276 |
72.4493 |
72.4541 |
0.3160 |
0.2964 |
| 0.147685 |
41.3200 |
41.3232 |
0.0438 |
0.0221 |
0.259993 |
72.8188 |
72.8241 |
0.4101 |
0.3904 |
| 0.200480 |
41.6899 |
41.6942 |
0.1094 |
0.0879 |
0.280131 |
73.1882 |
73.1939 |
0.5124 |
0.4924 |
| 0.242359 |
42.0596 |
42.0648 |
0.1928 |
0.1715 |
0.299006 |
73.5574 |
73.5636 |
0.6224 |
0.6022 |
| 0.278293 |
42.4290 |
42.4351 |
0.2914 |
0.2700 |
0.316846 |
73.9263 |
73.9330 |
0.7398 |
0.7193 |
| 0.310355 |
42.7981 |
42.8050 |
0.4034 |
0.3818 |
0.333816 |
74.2950 |
74.3022 |
0.8642 |
0.8433 |
| 0.339643 |
43.1668 |
43.1745 |
0.5277 |
0.5059 |
0.350044 |
74.6634 |
74.6712 |
0.9953 |
0.9740 |
| 0.366821 |
43.5349 |
43.5435 |
0.6635 |
0.6414 |
0.365626 |
75.0314 |
75.0398 |
1.1330 |
1.1111 |
| 0.392330 |
43.9025 |
43.9119 |
0.8102 |
0.7876 |
0.380644 |
75.3992 |
75.4082 |
1.2770 |
1.2545 |
| 0.416475 |
44.2694 |
44.2797 |
0.9673 |
0.9442 |
0.395161 |
75.7666 |
75.7762 |
1.4271 |
1.4039 |
| 0.439481 |
44.6356 |
44.6468 |
1.1344 |
1.1106 |
0.409231 |
76.1335 |
76.1440 |
1.5832 |
1.5591 |
| 0.461519 |
45.0009 |
45.0131 |
1.3111 |
1.2865 |
0.422898 |
76.5001 |
76.5114 |
1.7452 |
1.7200 |
| 0.482722 |
45.3653 |
45.3787 |
1.4972 |
1.4716 |
0.436200 |
76.8662 |
76.8785 |
1.9129 |
1.8865 |
| 0.503194 |
45.7287 |
45.7435 |
1.6925 |
1.6655 |
0.449169 |
77.2318 |
77.2454 |
2.0863 |
2.0582 |
| 0.523022 |
46.0910 |
46.1075 |
1.8967 |
1.8680 |
0.461834 |
77.5969 |
77.6119 |
2.2651 |
2.2350 |
| 0.542277 |
46.4521 |
46.4707 |
2.1096 |
2.0787 |
0.474220 |
77.9615 |
77.9783 |
2.4494 |
2.4167 |
3.3 空间啮合传动弹性共轭曲面的求解
3.3.1 变形基本曲面的求解
由变形基本曲面运动基本方程(2-7-1)及已知的一个变形基本曲面,可求得另一变形基本轭曲面。

式中u、v为曲面参变量,f(u,v,φ1)=0为(2-7-1)式的参数表达式。
3.3.2 变形的求解
空间啮合时,变形基本曲面上每一瞬时的接触线方程可以求出,在某一瞬时的接触线上各点的变形便可以求出。整个齿面各点的变形就是所有接触线变形的集合。
S={δ|δ={δ所有接触线}}
空间啮合时,接触线上各点弹性变形的求解是三维弹性接触问题的变形求解,目前较多的是采用有限元或边界元方法,这方面已有一些研究[78],但仍缺乏较成功的计算软件。由于三维弹性接触问题变形的求解涉及的因素较复杂,一般很难给出变形计算的拟合公式,某些空间啮合传动(如斜齿圆柱齿轮传动)虽可以得出变形计算拟合公式[54],但拟合公式仍较复杂,且计算精度较低。随着三维弹性接触问题变形求解研究的发展,将进一步提高弹性共轭曲面求解的精度。
3.3.3 弹性共轭曲面的求解
r(i)(u,v)=rd(i)(u,v)+δ(i)(u,v) (i=1,2)
其中 δ(u,v)=δp(u,v)+δb(u,v)
δp(u,v)为接触变形矢量,δb(u,v)为法向挠曲变形矢量。
弹性共轭曲面Σi就是各离散点r(i)(u,v)的集合。

3.3.4 鼓形齿联轴器弹性共轭齿面求解方法
共轭齿面鼓形齿联轴器由渐开线直齿圆柱内齿轮和与之共轭的相同齿数的外齿轮组成。内外齿轮轴线有一轴间倾角θ,其传动原理如图1-2所示。以下根据空间啮合弹性共轭曲面的求解方法,讨论在已知作用转矩下的内外齿轮弹性共轭齿面求解方法。
3.3.4.1 变形基本曲面
1.坐标系(如图3-2所示)
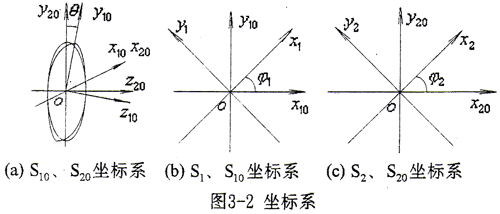
S1(o,x1,y1,z1)坐标系,为与外齿轮固连的动坐标系;z1轴与外齿轮轴线重合。
S10(o,x10,y10,z10)坐标系,为过渡坐标系;z10与z1轴重合;x10与x1夹角φ1为某瞬时外齿轮转角。当φ1=0时,S10系与S1系重合。
S2(o,x2,y2,z2)坐标系,为与内齿轮固连的动坐标系;x2为某一齿槽和齿宽中线;z2轴与内齿轮轴线重合。
S20(o,x20,y20,z20)坐标系,为静坐标系;z20轴与z2轴重合;x20轴与x2轴夹角φ2为某瞬时内齿轮转角,φ2=0时,S20系与S2系重合。
四个坐标系有共同的原点O,x10与x20轴线重合,z10与z20轴线夹角为两齿轮轴线的轴交角θ(y10与y20轴线夹角亦为θ)。
2.坐标转换关系
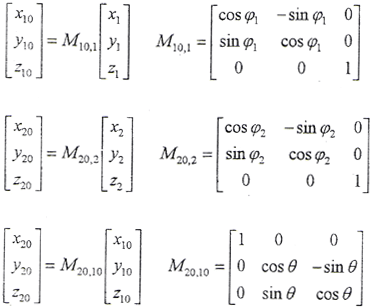
坐标的逆变换可由它们的逆矩阵导出。
3.内齿轮变形基本曲面方程
设内齿轮变形基本曲面为渐开线曲面,其端面上的齿面线及坐标如图3-3所示。
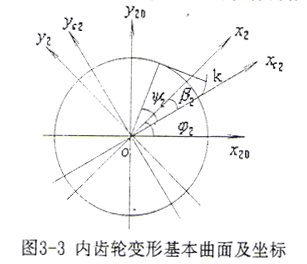
xc2轴通过渐开线在基圆上的起点。(o,xc2,yc2,zc2)坐标系下的曲面方程为

式中 ψ2、t2——曲面参变量;rb——渐开线基圆半径。设α2为曲面某一点K处的压力角,则有ψ2=tgα2。将(3-3-2)式转换到S20坐标系,方程为

式中λ2=ψ2-β2+φ2
β2——内齿轮基圆齿槽宽所对圆心角之半。
β2=π/(2z)+(2xr2tgα+xτ2)/z+tgα-α
式中 xr2——径向变位系数
xτ2——切向变位系数
(3-4-2)式就是在S20系的内齿轮变形基本曲面方程。
4.外齿轮变形基本曲面方程
由 n·[(ω(2)-ω(1))×rd(2)]+n·(ω(1)×a12)-n·da12/dt=0,不计轴系的变形,da12/dt=0,相交轴传动a12=0,有
n·[(ω(2)-ω(1))×rd(2)]=0 (3-3-4)
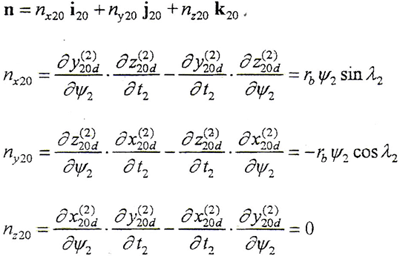
所以 n=rbψ2(sinλ2i20-cosλ2j20)
令|ω(2)|=|ω(1)|=1,则ω(2)=k20,ω(1)=-sinθj20+cosθk20。
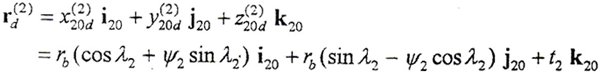
将n、ω(2)、ω(1)、rd(2)代入(3-3-4)式,得
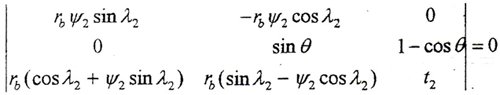
化简得
t2sinλ2sinθ-rb(1-cosθ)=0 (3-3-5)
(3-3-5)式就是本问题的弹性共轭曲面运动基本方程,它是关于t2、ψ2、φ2的函数,可表示为f(t2,ψ2,φ2)=0
外齿轮变形基本曲面方程r1d(1)为

令φ1=φ2=φ,将M1,2、r2d(2)及f(t2,ψ2,φ2)=0解出的φ代入(3-3-6)的第三式,则可得到以t2、ψ2为参变量的外齿轮曲面的表达式。
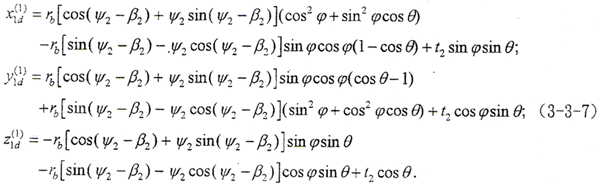
其中 t2=rb(1-cosθ)/[sin(ψ2-β2+φ)sinθ]
为了求解变形,还需求得内齿轮轮齿另一齿面的变形基本曲面方程,如图3-4所示。
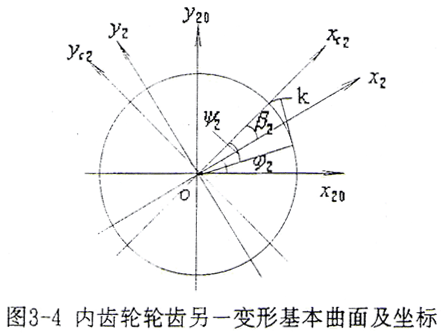
(o,xc2,yc2,zc2)坐标系下的曲面方程为

用与前述相同的方法可求得以t2、ψ2为参变量的外齿轮轮齿另一齿面的变形基本曲面方程为
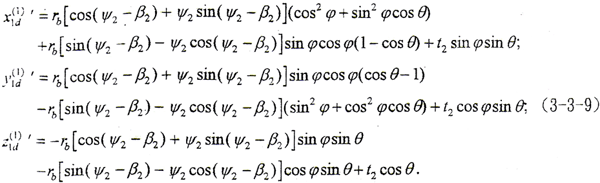
其中 t2=rb(cosθ-1)/[sin(ψ2-β2+φ)sinθ]
3.3.4.2 求解变形
本文简要介绍采用边界元法求解鼓形齿联轴器内外齿轮轮齿变形的方法。
1.三维弹性问题边界元法的基本理论[114][115]
三维弹性问题边界元法是根据线弹性力学的基本方程及边界条件和虚功互等定理或加权余量概念,导出边界积分方程,再将边界积分方程离散,把所解问题定义域的边界划分为若干单元,然后在每个单元上利用插值公式把边界未知量表示成依赖于节点未知量的函数。对于三维域上定解问题而言,需离散的区域仅为二维的边界面。对于边界上每个节点建立线性代数方程,形成一代数方程组。求解这个方程组,即可解得各节点的未知位移和应力值。三维弹性接触问题的边界元法[78],是运用三维弹性问题边界元法,以接触体为研究对象,考虑光滑条件、平衡条件、位移协调条件和单侧条件等接触边界条件,求解接触问题的结点未知位移和应力值。其求解过程,必须首先给定初始接触区,再根据计算判断接触区是否满足接触区判定准则,若不满足,再进行接触区调整,直到满足接触区判定准则,即可求得各节点的未知位移和应力值。
2.边界元模型
本论文不讨论三维弹性接触问题的求解方法,着重于应用三维弹性接触问题边界元法来求解鼓形齿联轴器内外齿轮齿面的弹性共轭曲面。为了求解变形基本曲面的变形,首先要确定其数值模型,进行单元的划分。
设内齿轮为主动轮,将一轮齿从左右齿槽中点到轮体外圆以轴截面取出,如图3-5所示。在轮体截取面上作用均布力,其约束为绕齿轮轴线转动而不能有轴向位移。外齿为从动轮,将一轮齿从左右齿槽中点到齿轮内孔以平行于轮齿中线和齿轮轴线的平面取出,如图3-6所示。截面上的面力为未知,其约束为各方向位移为零。
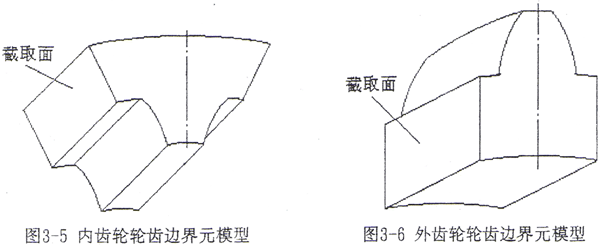
以上的轮齿边界元模型与实际的约束和加载情况较接近。当计算精度有更高要求时,可适当扩大取出体范围。显然,扩大的模型必须划分更多的单元,计算量更大。
接触问题的边界单元划分有其特殊的要求,一般对于非接触区域根据精度要求划分较大单元。由于接触的可能区域在接触线附近,因此,需在接触线附近适当划分较小的单元,以满足计算中接触区域的调整,求得较精确的变形值。
3.3.4.3 弹性共轭曲面
设在齿面某一点rd(i)的法向变形为δ(i),则该点的弹性共轭曲面数值解为
r(i)=rd(i)+δ(i)n0(i)
式中n0(i)为齿面的外法线单位矢量。
整个齿面的弹性共轭曲面为所有数值解的集合
Σ={r|r={r(i)全体齿面点}}
3.4 多齿啮合的弹性共轭曲面
前面我们所讨论的是两弹性体单对曲面连续接触运动的弹性共轭曲面问题的求解,它是弹性共轭曲面问题求解的基础。在工程实际中,大量地存在两弹性体有多对曲面同时接触运动,且同时接触的曲面对数有规律地变化,如切削加工的多刀刃切削和齿轮传动中的多齿啮合等等。由于弹性体多对曲面接触时的载荷分配与曲面的几何特征相互作用及多对曲面接触的数目变化的过渡,它与在刚性条件下的共轭曲面与共轭运动的关系不同。研究在弹性条件下,多对共轭曲面与共轭运动的关系,有重要的理论和现实意义。本节以齿轮传动为例,讨论弹性体多对齿面啮合的弹性共轭曲面问题。
3.4.1 坐标系及齿面
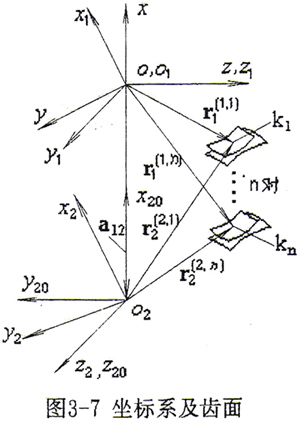
坐标系及齿面如图3-7所示。
坐标系S1(o1,x1,y1,z1):与轮1固连的动坐标系;
坐标系S2(o2,x2,y2,z2):与轮2固连的动坐标系;
坐标系S(o,x,y,z):静坐标系;
坐标系S20(o2,x20,y20,z20):过渡坐标系。
设当前同时有n对齿啮合,k1、k2…kn为各齿对接触参考点。rl(m,n)表示在l坐标下齿轮m的第n对齿的接触参考点径矢。
3.4.2 各齿对相对运动
由第二章分析知,某一齿对的相对运动为
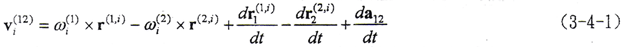
式中 vi(12)——第i对齿面相对运动速度矢量
ωi(1)ωi(2)——齿轮1、齿轮2上第i对齿面的角速度矢量
不考虑轴系的变形,有

将(3-4-2)、(3-4-3)、式代入(3-4-1)式,得
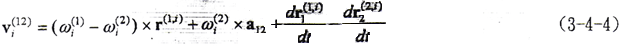
 分别为两齿轮第i对齿面参考点相对于S1、S2坐标系的弹性变形速度矢量。
分别为两齿轮第i对齿面参考点相对于S1、S2坐标系的弹性变形速度矢量。
3.4.3 多齿对弹性共轭曲面运动基本方程
根据弹性共轭曲面基本概念,有
ni·vi(12)=0
即
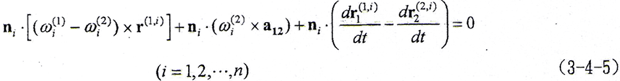
在不同的多齿啮合状态,运用(3-4-5)式,有不同的参数间的影响情况,以下将多齿啮合状态分为多齿接触对数稳定状态和多齿接触对数变化过渡状态两种情况分别讨论。
3.4.4 多齿接触对数稳定状态的弹性共轭曲面
3.4.4.1 多齿接触对数稳定状态,各接触齿对的参考点在该状态任一瞬时各齿对都处于最大变形状态,不存在变形开始的初期阶段和变形的恢复阶段。因此,在这个阶段,各接触齿面参考点都处于变形已结束,回弹尚未开始的状态。很显然,在此状态有

另一方面,该状态下的任一瞬时,两齿面参考点的运动应与各自齿轮的运动相吻合,否则与前述要求矛盾,因此有

综合以上分析,将(3-4-6)、(3-4-7)式代入(3-4-5)式有
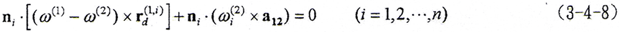
式中 rd(1,i)为接触参考点在最大变形状态的径矢。
(3-4-8)式就是多齿接触对数稳定状态的弹性共轭曲面啮合基本方程。
3.4.4.2 多齿接触对数稳定状态的弹性共轭曲面求解
由(3-4-8)式知,它与单对齿啮合的弹性共轭曲面的求解类似。但由于它是多对齿同时啮合,啮合齿对的变形求解与每对齿的承受的载荷有关,因此变形的计算要复杂得多。
1.变形基本曲面的求解
变形基本曲面为在变形最大情况下由弹性共轭啮合点构成,它是在整个啮合过程中逐渐形成的动态曲面。设rd(1,i)已知,则由齿轮轮齿在轮体上的等分性,Σd(1,i-1)、Σd(1,i+1)为在Σd(1,i)前后相差一个齿距角的位置上,因此不难给出rd(1,1)、rd(1,2)、…rd(1,n)的方程。
不妨将(3-4-8)式写成如下形式
f(u,v,φ1)=0 (3-4-8a)
式中u、v为曲面参变量,φ1为运动参数。
根据共轭曲面求解方法,可求得与rd(1,i)(i=1,2,…,n)共轭的变形基本曲面rd(2,i)(i=1,2,…,n)。

2.变形的求解
由三维弹性接触问题的边界元法可以求出各共轭接触点的最大变形。但这是一个非连续多区域接触问题,从理论上讲,它可能发生接触的边界Γck分别为Γc(k,1)、Γc(k,2)、…、Γc(k,n),它们分别满足滑动边界和自由边界的条件。确定适当的数值模型及边界积分方程的离散,同样可以算出各自的变形。显然多齿啮合状态的边界元模型较单对齿啮合要复杂得多,尤其当啮合齿对较多时,模型更为复杂。这种情况的三维弹性接触问题的边界元方法尚未见有文献报道,相信随着边界元方法的发展,这个问题将能得到解决。
整个多齿接触对数稳定状态的弹性共轭曲面的变形的计算,不需要象单对齿啮合那样径历整个啮合过程,因为根据弹性共轭点的一一对应性,某一对齿在某一位置的啮合状况与另外任一齿在该位置的啮合状况是一致的。因此只要将n对同时啮合的齿对的啮合状况的并集作为整个多齿接触对数稳定状态全过程,就可以以并集的方式得到这个过程中整个曲面的变形解。
3.弹性共轭曲面
设变形基本曲面上一点rj(k,i)=rdj(k,i)+δj(k,i)·n0j(k,i)
式中n0j(k,i)为曲面外法线单位矢量。
整个齿面的弹性共轭曲面为所有数值坐标的集合
r={rj|j为所有多齿接触对数稳定状态区间齿面点}
值得指出的是,当多齿接触对数n不同,虽然都是处于多齿接触对数稳定状态,但由于承担载荷的齿对数不同,其变形也不同。因此,应该对n不同的区域分别求解。
3.4.5 多齿接触对数变化过渡状态的弹性共轭曲面
若齿轮传动形式所确定的弹性条件下多齿接触对数为已知,设此数目为m和n。则啮合过程中必然经历m对齿啮合→n对齿啮合和n对齿啮合→m对齿啮合这样的过渡状态。设m<n,则前一种情况就是有齿对啮入而无齿对啮出,后一种情况就是有齿对啮出而无齿对啮入。无论在哪一种过渡状态都存在变形的不稳定状态,啮入的过程中,啮入齿对经历了从无变形到最大变形的变形初始阶段,啮出齿对经历了从最大变形到无变形的变形恢复阶段。
3.4.5.1 过渡状态的弹性共轭曲面啮合基本方程
在过渡状态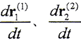 都不为零,因此对啮入和啮出齿面,啮合基本方程为
都不为零,因此对啮入和啮出齿面,啮合基本方程为
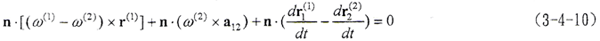
3.4.5.2 过渡状态弹性共轭曲面分析
1.啮入过程
在啮入过程中,啮入齿面经历了从无变形到最大变形的过程。在啮入的最初瞬时,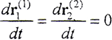 ,(3-4-10)式成为
,(3-4-10)式成为

(3-4-11)的形式与(3-4-8)的形式相同,但由于所处的受力变形状态不同,二者是有差别的。(3-4-8)式的曲面参考点径矢为rd,它表示处于最大变形状态下的参考点径矢,该点的弹性共轭曲面点为rd+δ·n0。而(3-4-11)式的曲面参考点径矢r,它表示处于无变形状态下的参考点径矢,即它就是该瞬时的弹性共轭点。很显然,啮入瞬时的共轭接触点少了δ·n0一项。通常啮入过程从主动轮齿根与从动轮齿顶接触开始,传统的齿廓修形方法认为应该在齿顶和齿根修形。这里从弹性共轭曲面理论方面定性地证明了传统的齿廓修形位置的正确性。
2.啮出过程
在啮出过程中,啮出齿面经历了从最大变形到无变形的变形恢复过程,其过程为啮入过程的逆过程,其机理与啮入过程相似。当啮出齿对运动到主动轮和被动轮的齿距不等于变形基本齿面的节距位置,啮合过程就开始了。在变形的恢复开始瞬时,仍处于变形最大的啮合齿对的弹性共轭曲面要根据当前瞬时的载荷分配进行计算,这与啮入的情况是相同的。在啮出的最后一刻,由于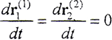 ,此时的情况与啮入的最初瞬时相同。
,此时的情况与啮入的最初瞬时相同。
上一页
下一页


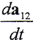 =0,由(2-7-1)式得
=0,由(2-7-1)式得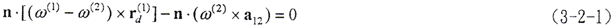

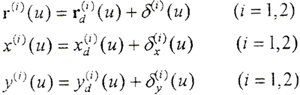
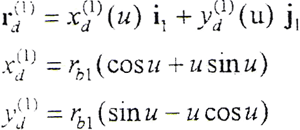
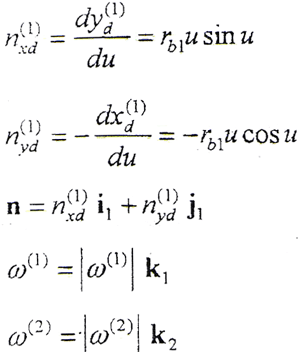
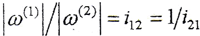

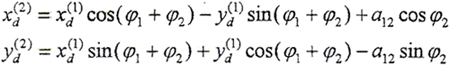
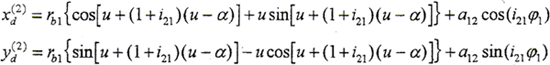

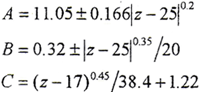
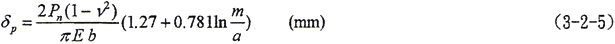
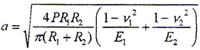
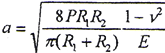
 ,曲率半径为
,曲率半径为 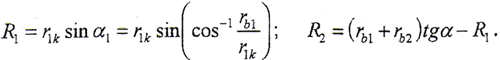
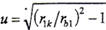 ,即可得到以u为参变量的变形量离散值δ(1)(u)=δp(1)(u)+δb(1)(u)、δ(2)(u)=δp(2)(u)+δb(2)(u)
,即可得到以u为参变量的变形量离散值δ(1)(u)=δp(1)(u)+δb(1)(u)、δ(2)(u)=δp(2)(u)+δb(2)(u)


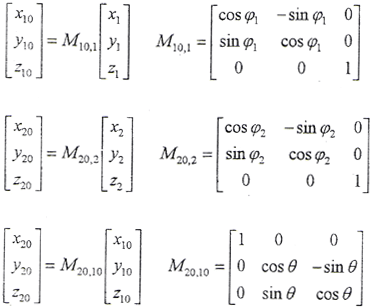



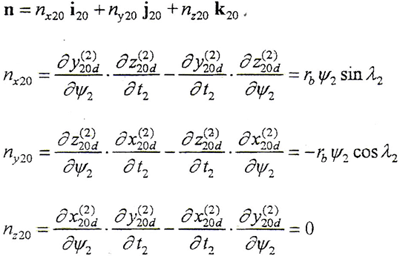
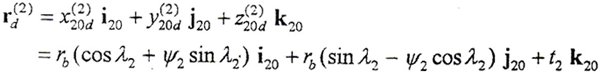
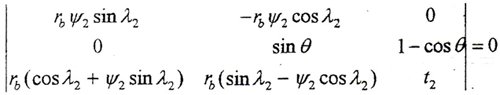

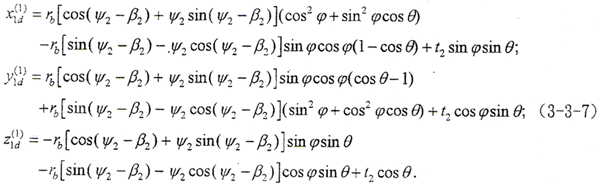


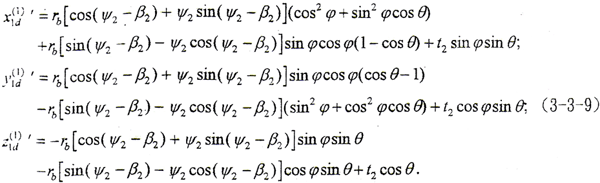


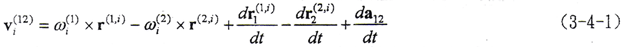

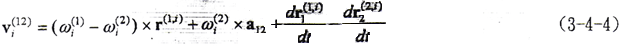
 分别为两齿轮第i对齿面参考点相对于S1、S2坐标系的弹性变形速度矢量。
分别为两齿轮第i对齿面参考点相对于S1、S2坐标系的弹性变形速度矢量。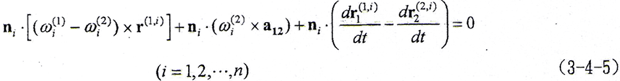


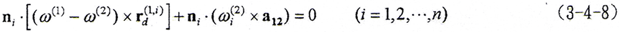

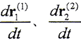 都不为零,因此对啮入和啮出齿面,啮合基本方程为
都不为零,因此对啮入和啮出齿面,啮合基本方程为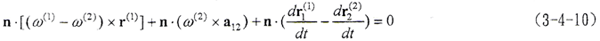
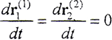 ,(3-4-10)式成为
,(3-4-10)式成为