第七章 鼓形齿联轴器多齿啮合实验
7.1 概述
从前几章的分析可以看出,鼓形齿联轴器具有复杂的空间啮合机理。尤其对于非共轭鼓形齿联轴器,在安装时有轴间倾角存在的情况下,理论上未受载时只有两对齿接触。而在载荷作用下,轮齿受力产生变形,则可能出现多对齿接触。在特定载荷下,有多少对齿接触,各接触齿对的受力分布如何,是设计鼓形联轴器需考虑的极为重要的因素。以往在设计时都是以在额定载荷作用下有一半齿接触平均受力为依据的非常粗略的估算方法来校核鼓形齿联轴器强度的。在具有轴间倾角的情况下,在不同的齿轮周向位置上,齿面啮合点的齿高和齿向位置是不相同的,而对于内外齿轮轮齿来说,其各不同位置的啮合刚度存在较大差异。另外,微小的齿面曲率干涉、齿轮的制造误差、联轴器的安装误差等偶然因素的影响,使实际的啮合齿对数和受力的分布变得更加复杂,理论计算非常困难。因此,用实验手段对鼓形齿联轴器进行测试,分析研究其在特性载荷下的啮合对数和受力的分布趋势具有非常重要的意义。
到目前为止,还未见有关此内容的实验研究报道。本文运用应变测量法对鼓形齿联轴器进行多齿啮合实验研究。实验的主要目的,一是要得出鼓形齿联轴器的实际接触齿对数及受力分布趋势的结果,二是验证优化鼓度曲线的非共轭齿面鼓形齿联轴器的啮合特性。
7.2 电阻应变测量基本原理[125]
导体或半导体材料在外界力作用下产生机械变形,其电阻值将发生变化,这种现象称为“应变效应”。把依据这种效应制成的应变片粘贴于被测材料上,则被测材料受外界作用力所产生的应变就会反应到应变片上,从而使应变片上的电阻丝的阻值发生变化,通过测量阻值的变化量,就可以反映出外界作用力的大小。
电阻应变片常用金属材料有康铜、镍铬合金、镍铬铝合金(卡码合金),它们具有不同的灵敏系数和线膨胀系数。以上材料中,康铜用得最多,因为它的灵敏系数k对应变的稳定性非常高,不仅在弹性变形范围内保持常数,而且进入塑性变形范围内仍基本保持常数,所以测量范围大。另外,康铜的电阻温度系数小且稳定,因而测量时温度误差小。本实验采用康铜材料的金属电阻应变片,灵敏系数为2.08。
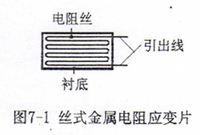
金属电阻应变片有丝式应变片和箔式应变片等不同形式。本实验采用丝式应变片,其结构如图7-1所示。它是用一根金属细丝按图示形状弯曲后用胶粘剂贴于用纸或有机聚合物薄膜等材料制成的衬底上,电阻丝两端焊有引出线。
应变片的粘贴质量对试件的变形是否能有效地传递有直接影响,因此在使用应变片时,应选用性能良好的粘结剂,并注意做到整片粘贴牢固。
7.3 鼓形齿联轴器多齿啮合测试方法
7.3.1 实验装置设计
本实验装置主要用于测试鼓形齿联轴器静态多齿啮合受力分布状态。设计时主要考虑以下几个因素:
(1)装置的结构能进行不同载荷、不同工作轴间倾角及不同型号鼓形齿联轴器的测试;
(2)装置具有足够的强度刚度;
(3)装置的结构简单,制造方便,成本低,易于安装和调整。
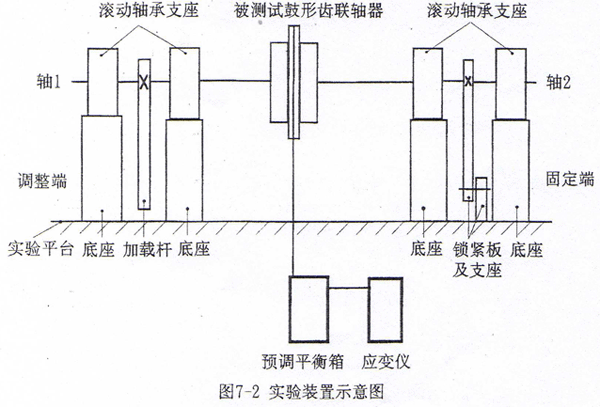
实验装置简图如图7-2所示,实验装置实物照片见附录。实验装置由固定端和调整端组成。被测试鼓形齿联轴器的两个外齿轮分别装于轴1和轴2上。轴1、轴2分别由两个滚动轴承支承。轴1上安装有加载齿轮,加载杆上装有与加载齿轮模数齿数相同的内齿轮,便于调整加载杆的位置。轴2上装有锁紧板,锁紧板与止动支座联接,以承受所加的转矩。这样,当加载杆端头加载时,被试鼓形齿联轴器即承受所加转矩的作用。安装时保持轴1、轴2水平等高。当两轴在水平面内同轴线时,则被测试鼓形齿联轴器内外齿轮同轴线,无轴间倾角。当调整端平行移动一个距离,则内齿轮与两外齿轮产生相同的轴间倾角。几何关系如图7-3所示。

式中 θ——轴间倾角
d——水平偏移距离
l——两外齿轮中截面轴向距离

7.3.2 实验方案
鼓形齿联轴器内外齿轮的啮合齿对承受所作用的转矩的作用。一般情况下,内齿轮轮齿的刚度大于外齿轮轮齿的刚度[33][34][37],为了能更有效地反应应变,工作应变片贴于外齿轮轮齿的端面,温度补偿应变片贴于不受力的相同材料上。轮齿的应力状态较复杂,在齿根处还存在应力集中。但总的来说,对于一个齿,其齿根主应力分布[118]如图7-4所示,因此考虑工作应变片贴于轮齿中心线受拉应力的一侧,靠近齿根b边缘处。这样既不影响齿的啮合,又能有效地反应接触状况,贴片布局见图7-5所示。由于轮齿端面位置较为狭小,无法贴两片应变片,因此采用单臂工作方式测试。
试件的选择应考虑加载量及贴片方便两方面的因素,选择模数较大的试件,便于贴片操作,但所需要加的载荷也较大,给操作带来困难;反之则加载方便,但贴片较困难。综合考虑上述两方面的因素,并考虑实验能反映工业应用的实际情况,本实验选用实际使用的鼓形齿联轴器为试件,m=3mm,z=56,齿轮制造精度为级-8,两个鼓形齿轮分别为圆弧鼓度曲线和优化鼓度曲线。

由于试件的齿数较多,并考虑鼓形齿联轴器受力作用时力分布的对称性,本实验采用一半齿间隔一齿贴片的方法,测试数据对称处理,并改变齿轮的周向安装位置校核其对称性。
7.3.3 实验仪器
本实验使用两套YJ——5型静态应变仪及20个点的预调平衡箱,同时连接两鼓形齿轮的共30只应变片进行测试。
7.3.4 实验步骤
(1)在两外齿轮轮齿设定的位置和不受力的同种材料上,进行表面处理,粘贴工作应变片和温度补偿应变片,焊接并固定引线;
(2)按照轴间倾角要求安装好试验装置和被测鼓形齿联轴器;
(3)将各被测轮齿测点处的应变片引线按要求连接在预调平衡箱上,按通电源,粗调平衡。摇动引线,应变仪指示器应无明显摆动,否则导线或接线可能存在问题。逐点触摸应变片,都应有受温度变化引起的应变产生,指针发生偏摆,以此可检查应变片接线是否可靠和接线位置是否正确;
(4)支起加载杆,逐点进行预调平衡;
(5)加载,测量并记录数据;
(6)若要改变轴间倾角或载荷,应重新调整实验装置,然后重复(4)、(5)步骤。
7.4 鼓形齿联轴器多啮合实验数据分析
通过对被测试件的不同轴间倾角及不同载荷的多种实验参数组合的测试,取得多组实验数据,测试数据如表7-1所给。将测点的圆周位置和应变量以极坐标绘图,如图7-6所示。
表7-1 多齿接触实验数据记录(应变量με)
| 模数m=3mm 齿数z=56 压力角α=20° 齿宽b=30mm 鼓度曲线:圆弧 |
| 齿对号 |
轴倾角
θ=0°
转矩
T=1700Nm |
轴倾角
θ=0.5°
转矩
T=1700Nm |
轴倾角
θ=1.0°
转矩
T=1700Nm |
轴倾角
θ=1.5°
转矩
T=1700Nm |
轴倾角
θ=1.8°
转矩
T=1200Nm |
轴倾角
θ=1.8°
转矩
T=400Nm |
| 1 |
15.0 |
13.0 |
9.0 |
7.0 |
0.0 |
0.0 |
| 3 |
15.0 |
14.0 |
9.0 |
7.0 |
0.0 |
0.0 |
| 5 |
11.0 |
11.0 |
11.0 |
6.0 |
0.0 |
0.0 |
| 7 |
11.0 |
10.0 |
10.0 |
5.0 |
0.0 |
0.0 |
| 9 |
9.0 |
12.0 |
12.0 |
11.0 |
2.0 |
0.0 |
| 10 |
8.0 |
11.0 |
16.0 |
21.0 |
3.0 |
0.0 |
| 11 |
7.0 |
13.0 |
21.0 |
23.0 |
2.0 |
2.0 |
| 13 |
6.0 |
16.0 |
26.0 |
41.0 |
6.0 |
1.0 |
| 15 |
8.0 |
17.0 |
30.0 |
42.0 |
6.5 |
5.0 |
| 17 |
7.0 |
13.0 |
26.0 |
36.0 |
12.0 |
10.0 |
| 19 |
8.0 |
12.0 |
23.0 |
23.0 |
17.0 |
9.0 |
| 21 |
6.0 |
9.0 |
11.0 |
13.0 |
0.0 |
0.5 |
| 23 |
11.0 |
11.0 |
11.0 |
13.0 |
0.0 |
0.0 |
| 25 |
7.0 |
6.0 |
4.0 |
4.0 |
3.0 |
0.0 |
| 27 |
13.0 |
10.0 |
5.0 |
4.0 |
0.0 |
0.0 |
| 29 |
15.0 |
13.0 |
9.0 |
7.0 |
0.0 |
0.0 |
| 模数m=3mm 齿数z=56 压力角α=20° 齿宽b=30mm 鼓度曲线:双曲线 |
| 齿对号 |
轴倾角
θ=0°
转矩
T=1700Nm |
轴倾角
θ=0.5°
转矩
T=1700Nm |
轴倾角
θ=1.0°
转矩
T=1700Nm |
轴倾角
θ=1.5°
转矩
T=1700Nm |
轴倾角
θ=1.8°
转矩
T=1200Nm |
轴倾角
θ=1.8°
转矩
T=400Nm |
| 1 |
14.0 |
13.0 |
12.0 |
13.0 |
2.0 |
1.0 |
| 3 |
13.0 |
13.0 |
12.0 |
12.0 |
2.0 |
1.0 |
| 5 |
12.5 |
13.0 |
12.0 |
11.0 |
4.5 |
2.0 |
| 7 |
13.0 |
13.5 |
14.0 |
14.0 |
2.0 |
1.0 |
| 9 |
9.0 |
10.0 |
10.0 |
9.5 |
0.5 |
0.0 |
| 11 |
10.5 |
17.0 |
20.0 |
12.0 |
0.0 |
0.0 |
| 13 |
10.0 |
13.0 |
14.0 |
15.5 |
0.0 |
0.0 |
| 15 |
9.0 |
14.0 |
15.0 |
10.0 |
0.5 |
14.0 |
| 17 |
11.0 |
16.0 |
18.0 |
13.0 |
1.0 |
0.0 |
| 19 |
8.0 |
10.0 |
13.0 |
9.0 |
2.0 |
4.0 |
| 21 |
10.0 |
12.0 |
12.0 |
13.0 |
0.0 |
0.0 |
| 23 |
8.0 |
10.0 |
9.0 |
9.0 |
15.0 |
1.5 |
| 25 |
12.0 |
12.0 |
12.0 |
13.0 |
1.0 |
1.0 |
| 27 |
6.0 |
5.0 |
4.0 |
3.0 |
2.0 |
1.0 |
| 29 |
14.0 |
13.0 |
12.0 |
13.0 |
1.0 |
0.0 |
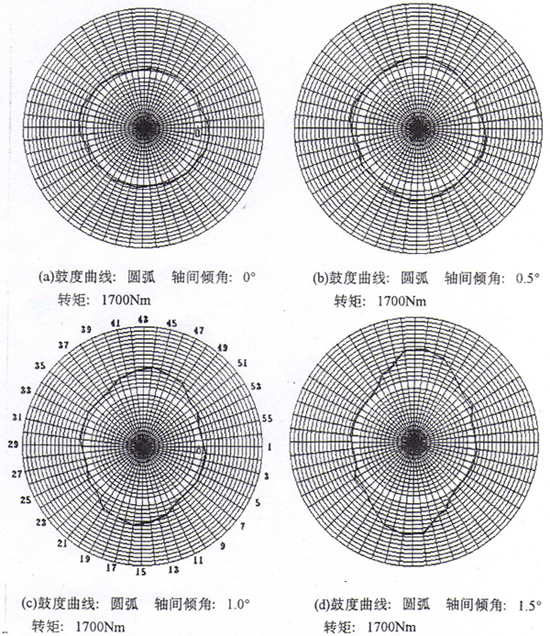
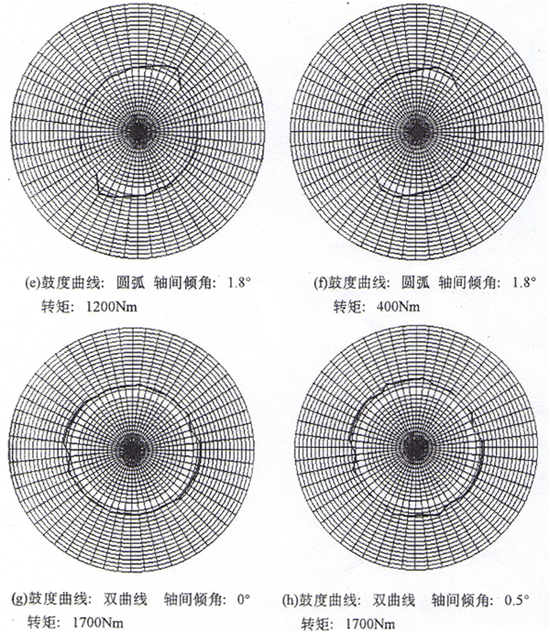
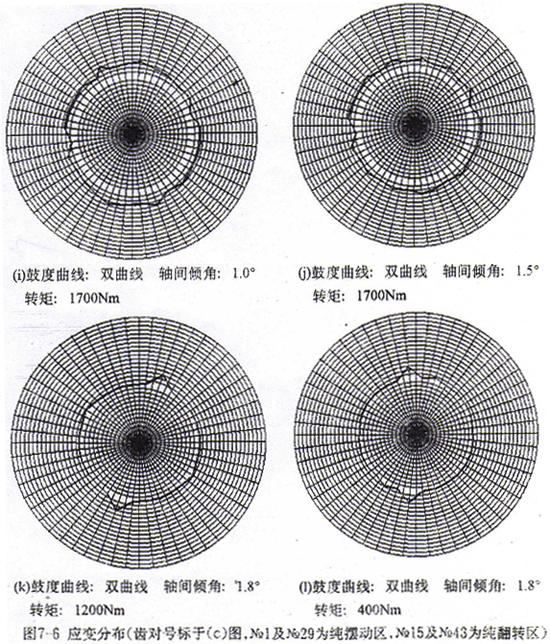
根据实验数据,可以分析得出以下结论:
1.在相同的最大轴间倾角下,随着转矩的增大,同时啮合的齿对数增加,当转矩达到某一值时(小于额定载荷),所有齿对啮合。这说明当转矩小于额定载荷时,就全部齿对啮合,而并非在额定载荷下只有一半齿对啮合,这一结论为首次得出,对鼓形齿联轴器的强度计算有重要参考意义。分析其原因,可以认为是偏载的影响。在有轴间倾角的情况下,最先接触的齿对在纯翻转区,而在此处,接触点处于偏离中截面最大位置,在这个位置上,轮齿的刚度比之于在中截面处要小得多,即在相同载荷作用下,所产生的变形要大得多。因此,在纯翻转区附近的齿对较容易产生变形而使相邻齿对接触;
2.在有轴间倾角存在的情况下,应变的分布以纯翻转区为最大,纯摆动区最小,约呈椭圆分布,这一方面是由于理论接触点在纯翻转区,另一方面是由于偏载的影响;
3.随着轴间倾角的增大,椭圆分布长短轴之差增大。理论上,在轴间倾角为零时,各轮齿应变应相同,但由于齿轮加工误差、安装误差、内外齿轮齿顶定位误差及贴片位置差异等因素影响,其应变分布并不是呈圆形分布,个别点甚至出现较大差异;
4.发生应变最大的齿位于偏离纯翻转区一角度处,这与理论计算结果[126]是一致的,因为从理论计算知,理论接触齿对正是位于此处;
5.圆弧鼓度曲线与优化鼓度曲线的测试结果相比较,在无轴间倾角的情况下,二者的最大应变无大的差异,只是分布状态有所不同,这是由各种误差的综合影响所造成的。当轴间倾角逐渐增大,应变分布的最大值和最小值之差逐渐增大,但优化鼓度曲线的差值变化较圆弧鼓度曲线的要小。当轴间倾角超过设计轴间倾角处于最大时,二者的最大应变量之比约为2;
6.由优化鼓度曲线的鼓形齿联轴器实验数据表明,在轴间倾角为设计角度时,应变量有均化趋势,即它比在更小的轴间倾角状态下的应变分布还要均匀,这是因为在设计角度下工作时,啮合状态与共轭条件相近,因而受力状态较均匀。本实验验证了优化鼓度曲线的鼓形齿联轴器具有优良的多齿啮合的受力分布特性。
上一页
下一页








