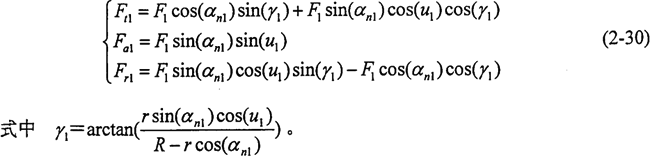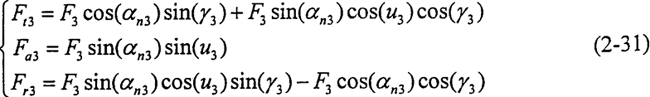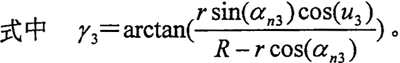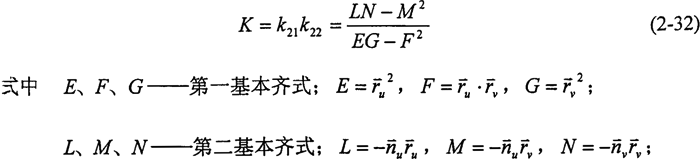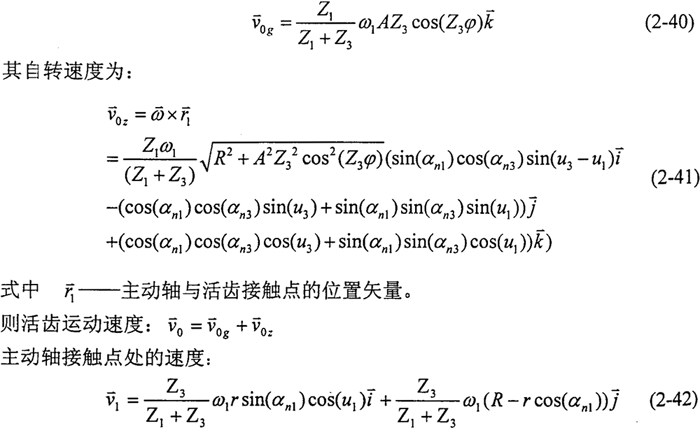2.4圆柱正弦活齿传动受力分析
2.4.1活齿受力分析
正弦滚道是由活齿沿一定的空间正弦曲线运动包格而成,所以圆柱正弦活齿传动属于空间啮合传动。在圆柱正弦活齿传动机构工作过程中,几乎所有的活齿都参与接触与传力,由于正弦滚道具有周期性,每个活齿与正弦滚道间共轭齿廓的工作过程又完全相同,所以在受力分析时,可以任选一个活齿啮合副作为对象进行研究。
不计活齿的重力及各构件间的摩擦力,则各构件对活齿的作用力都通过活去的球心并沿活齿齿面的法线方向,图2-10为各作用力的空间位置关系。活齿的局部坐杯系为(o;x,y,z),坐标原点0为活齿的球心,x轴为活齿传动的径向方向,y轴为活齿传动的周向方向,z轴为活齿传动的轴向方向。设主动轴的外正弦滚道对活齿的作用力为F1,接触角为αn1;壳体内正弦滚道对活齿的作用力为F3,接触角为αn3;导架的活齿槽对活齿的作用力为F2;ui(i=1,3)为各啮合副间瞬时接触线的方向角。
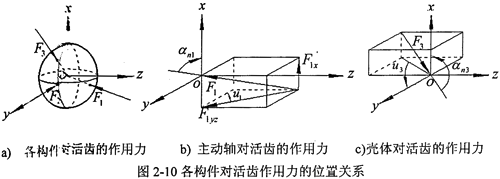
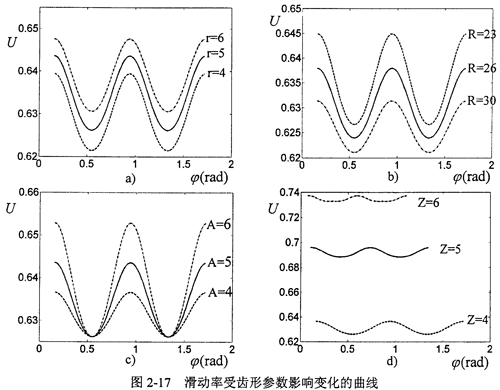
显然F1、F2、F3组成一空间汇交力系,假设活齿在每个工作瞬时处于衡状态,根据图2-10中各作用力的空间位置关系,可列方程如下:
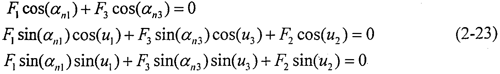
由式(2-23)可以看出,未知数包括F1、F2、F3、αn1、αn3共有5个,而方程个数只有3个,属于力学中静不定的问题,需要寻找变形协调条件来补足方程的个数。
为便于研究,找出其变形协调关系,做出如下假设:
(1)不计啮合点处的摩擦力与活齿自转;
(2)除啮合点处弹性变形外,其他各件的变形忽略不计,且变形服从胡克定律;
(3)各传动件轴向位移不计,加工误差忽略不计。
各活齿与主动轴之间的作用力F1i可分解为径向力F1xi,和径向法截面方向的力F1yzi,假定主动轴瞬时不动,给活齿施加一个顺时针方向的力矩T1(T1为输入力矩),在该力矩的作用下,各活齿与主动轴接触处产生接触变形,使活齿中心转过一个角度△φ,则所有活齿中心相应的发生一个相同的微小周向位移加,根据变形协调条件,假设△s在F1yzi方向的投影大小与F1yzi成正比,即F1yzi∝△scos(u1i),则有下列等式成立:

式中 F1yzi=F1isin(αn1); u1max=actan(R1/(AZ1));
R1——主动轴空间正弦曲线径向半径(mm);
A——空间正弦曲线的幅值(mm)
整理式(2-24)得到:

为求得F1yzmax,对主动轴列扭矩平衡方程,则有

式中 T1——输入扭矩(N·mm);
n——活齿个数。
将式(2-25)代入式(2-26)中得到:

现利用平均值法求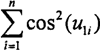 ,求解过程如下:
,求解过程如下:

另外,根据圆柱正弦活齿传动中一个活齿啮合副的几何关系,可列如下方程:
(r′-r)(cos(αn1)-cos(αn3))=R1-R3 (2-29)
式中 r′——正弦滚道半径(mm),通常r′=(1.04~1.11)r;
r——活齿半径(mm);
R3——壳体正弦曲线径向半径(mm)。
将式(2-23)、(2-25)及(2-29)联立,则方程的个数为5个,与未知数的个数相同,故可解。
2.4.2其他构件的受力分析
活齿对主动轴外正弦滚道作用力的圆周力分量Ft1、轴向力分量Fa1、径向力分量Fr1的大小分别为
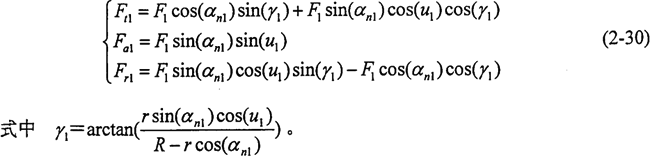
活齿对壳体内正弦滚道作用力的圆周力分量Ft3、轴向力分量Fa3、径向力分量Fr3的大小分别为
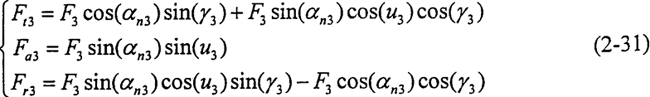
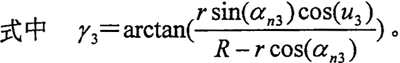
2.4.3圆柱正弦活齿传动受力分析计算实例
已知一圆柱正弦活齿减速器,其设计参数为A=4.5mm,r=5mm,r1=5.4mm,R=23.5mm,Z1=1,Z3=4,T=20Nm,t=5。根据本文建立的活齿受力分析模型,采用牛顿法求解式(2-23)、(2-25)及(2-29)联立的方程组,应用Matlab编程计算,得到在一个工作周期内活齿的受力情况,计算结果如图2-11、2-12所示。同时可计算出所有活齿作用在主动轴上轴向合图,其结果如图2-13所示。
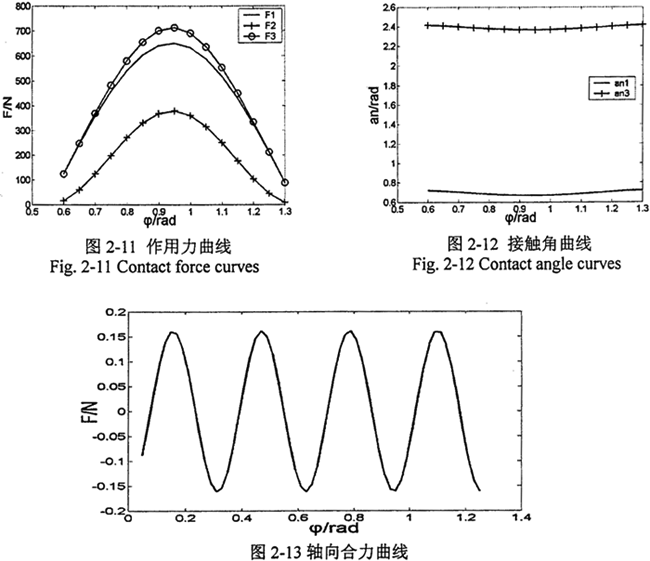
由图2-11分析可知,在空间正弦轨迹曲线的拐点附近活齿受力最大,且作用在活齿上的三个力F1、F2、F3中,F3值最大,也就是说,在进行接触强度计算的时候,应以活齿与壳体间的接触情况为主要依据。接触角αni(i=1,3)的求解为圆柱正弦活齿传动的结构设计提供了必要的条件,它成为正弦滚过深度bi,(i=1,3)的主要度量依据。由图2-13可以看出圆柱正弦活齿传动主动轴上的轴向合力几乎为零,且该传动输入轴的旋转中心与其几何中心重合,属于自平衡结构,避免了惯性力的产生。因此只需采用单激波器的结构型式即可使惯性力和作用力达到平衡,缩短了传动的运动链,减少了动力损耗,提高了传动系统的效率和运动稳定性。
2.5主曲率计算分析
在进行圆柱正弦活齿传动接触强度分析时,需要利用正弦滚道齿面的主曲盆和主曲率半径,为此需对正弦滚道齿面的主曲率和主曲率半径进行分析计算。根据微分几何理论,除在曲面上的奇异点之外,法曲率随着所选取的方向下同而变化,而在一个非奇异的固定点,沿不同方向的法曲率之中有其最大值和最小值,而这最大值法曲率和最小值法曲率及分别称为曲面在该点的两个主曲率,当主曲率不为零时,主曲率的倒数称为主曲率半径;对应主曲率的方向称为主方向,并且两个主方向互相垂直。
由于正弦滚道齿面是球状活齿沿空间正弦曲线轨迹运动包络而成,显见在理想情况下瞬时接触线的方向即为正弦滚道齿面的一个主方向,其对应的主曲k21=-1/r′,则另一个主方向应在瞬时接触线的法向方向,为得到正弦滚道凿面在该方向上的主曲率k22,需计算出正弦齿面在接触点处的全曲率K,由微分几何中对全曲率定义有:
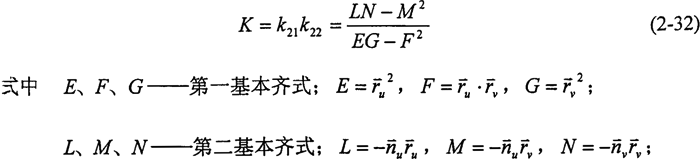

A——正弦幅值(mm);
Z——正弦滚道周期数;
R——活齿中心圆周方向旋转半径(mm);
u——瞬时接触线的方向角(rad);
v——接触角(rad);
φ——活齿在正弦滚道齿面坐标系中的位置角(rad)。
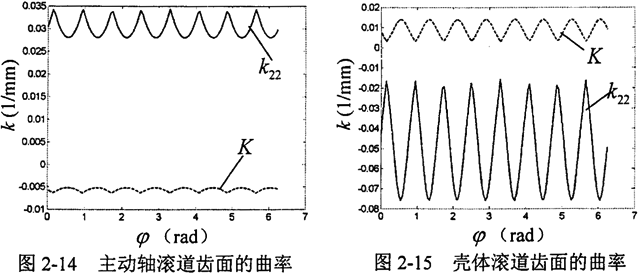
根据式(2-32),应用Matlab编程计算得到滚道齿面与活齿接触点处的主曲率与全曲率的变化曲线如图2-14、图2-15。从图中可见,主动轴正弦滚道齿面在接触点处的全曲率恒为负值,根据微分几何中的定义,则该接触点为双曲点,而壳体正弦滚道齿面在接触点处的全碘率恒为正值,则该接触点为随圆点。从数值上看,曲率的变化范围大,传动比较平稳。
2.6活齿的运动状态分析
在圆柱正弦活齿传动的一个活齿啮合副中,活齿与壳体及主动轴的滚道分别在A、B点接触,如图2-16所示,接触角近似取αn1=αn3=π/4,活齿在接触点A、B的运动速度方向即为接触点轨迹曲线LA及LB的切线方向,根据式(2-19),可知活齿与壳体接触点A的运动轨迹曲线LA的方程:

式中 R——活齿中心圆周方向旋转半径(mm);
r——活齿半径(mm)。

由式(2-33)可求得轨迹曲线LA的切线方程,为便于计算,将其转换到活齿坐标系中,该方程的方向数为:

在理想情况下,活齿的中心O沿空间正弦曲线运动,其轨迹曲线LO方程为:

同理,由式(2-35)可以求得活齿中心的运动速度方向,转换到活齿坐标系后,其方向数为:

根据空间解析几何中两空间直线夹角的公式,由式(2-34)、(2-36)可求出两轨迹曲线LA、LO切线的夹角αAO,通过计算证明αAO小于10°,忽略αAO引起的活齿相对壳体滚道齿面的滑移运动。同理可以求得两轨迹曲线LB、LO切线的夹角αBO,计算证明αBO较大,故不可忽略由αBO引起的活齿相对于主动轴滚道齿面的滑移运动。若将活齿中心O看作活齿运动的瞬时中心,则活齿在与壳体齿面接触点A的速度方向即为活齿在该点绕其自身轴线旋转的速度方向,活齿自转的旋转轴线应在垂直与该速度方向的平面上,也就是在壳体正弦滚道的法截面上。设旋转轴,即活齿自转角速度的方向矢量为:
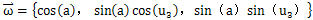
接触点的位置方向幺矢为:

则矢量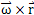 应平行于活齿中心的速度方向矢量{0,-tan(u3),1},据此条件,可以得到α=αn3-π/2。则旋转轴的方向矢量为:
应平行于活齿中心的速度方向矢量{0,-tan(u3),1},据此条件,可以得到α=αn3-π/2。则旋转轴的方向矢量为:
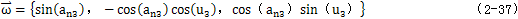
2.7滑动率
活齿传动在传递运动和动力的过程中,共扼齿廓高副两元素间,由于接触点的切线速度不同而产生相对滑动,齿形的磨损规律,在一定程度上取决于共轭齿廓在各接触点上相对滑动速度的变化律,滑动率U表明两共扼齿廓间有害滑动作用的特性。圆柱正弦活齿传动中相对速度为空间矢量,故本文中滑动率定义为两共轭齿廓瞬时接触线法线方向的相对滑动速度的变化律。一般情况下,活齿在滚道中的运动是比较复杂的,可作滚动、滑动、或又滑又滚,由对活齿运动状态的分析可知,圆柱正弦活齿传动中,齿面磨损相对严重的是活齿与主动轴这对共轭齿廓,活齿沿壳体齿面可作纯滚动或又滚又滑运动,而当活齿沿壳体齿面作纯滚动时,主动轴与活齿之间磨损最为严重,考虑此时主动轴与活齿之间的滑动率,即可以定性的分析圆柱正弦活齿传动共扼齿廓间的磨损情况。
根据本文对滑动率的定义,滑动率的公式可写为:
U=v10t/v1t (2-38)
式中v10t——主动轴与活齿接触点处沿接触线法线方向的相对滑动速度(m/s);
v1t——主动轴在接触点处沿接触线法线方向的相对滑动速度(m/s)。
当活齿沿壳体齿廓作纯滚动时,活齿绕自身轴线旋转的角速度为:

式中 ω1——主动轴旋转的角速度(rad/s)。
为便于计算,先假设导架固定不动,求得主动轴与活齿的在接触点处的相对速度矢量。活齿在与主动轴接触点处的运动速度为公转速度与自转速度两部分能合成速度,其中公转速度为活齿中心沿空间正弦轨迹曲线运动的速度:
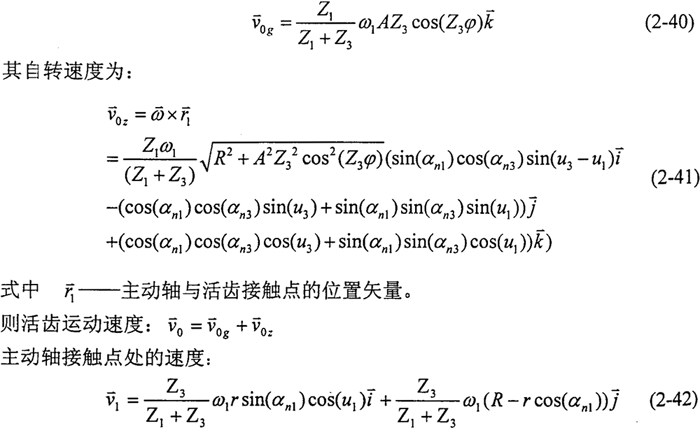
则主动轴与活齿的在接触点处的相对速度为:

在固定坐标系中,主动轴接触点处的速度为:
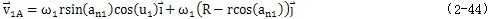
将相对速度矢量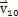 及主动轴接触点处的速度
及主动轴接触点处的速度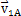 投影到瞬时接触线的法线方向得到v10t和,v1t,将二者代入式(2-38),计算出滑动率。由于正弦滚道形状具有周期性,因此共轭齿面间的滑动率也呈现周期性变化,考虑齿形参数——活齿半径r、活齿中心回转半径R、正弦幅值A及壳体滚道正弦周期数Z对滑动率的影响,若给定其中任意三个参数,改变另一个参数,可以得到在一个工作周期内滑动率随齿形参数的变化规律曲线如图2-17所示。
投影到瞬时接触线的法线方向得到v10t和,v1t,将二者代入式(2-38),计算出滑动率。由于正弦滚道形状具有周期性,因此共轭齿面间的滑动率也呈现周期性变化,考虑齿形参数——活齿半径r、活齿中心回转半径R、正弦幅值A及壳体滚道正弦周期数Z对滑动率的影响,若给定其中任意三个参数,改变另一个参数,可以得到在一个工作周期内滑动率随齿形参数的变化规律曲线如图2-17所示。
由此可见,圆柱弦活齿传动的滑动率是啮合点位置的函数,而且在一个工作周期滑动率变化不大。当活齿运动到正弦滚道的拐点处时,共轭齿面的滑动率最大;当运动到正弦滚道的波峰及谷处时,共轭齿面间的滑动率最小。由图2-17定性分析可知,参数r、R、A及Z对滑动率都有影响,其中壳体滚道正弦周期数Z的变化对滑动率的影响最大。进行结构设计时,当机构的传动比一定,在满足强度要求及其它设计要求的前提下,应适当减小钢球半径、增大活齿中心回转半径、减小正弦幅值,以达到降低滑动率,减小共轭齿廓间磨损的目的。
2.8本章小结
1.阐述了圆柱正弦活齿传动的结构组成和传动原理,推导出传动比计算公式及活齿传动的正确连续传动条件。建立空间正弦滚道齿面的齿廓方程,并仿真出齿廓曲面;
2.在单个活齿受力分析的基础上,根据变形协调条件,建立了圆柱正弦活齿传动的受力分析模型,据此可以计算出各构件作用在活齿上的接触力的数值角,并建立了该传动其他构件的受力计算公式,为圆柱正弦活齿传动的结构优化设计和强度分析提供了依据。由此也验证了圆柱正弦活齿传动是一具有自平衡能力的结构系统;
3.计算出正弦滚道齿面在与活齿齿面接触点处的全曲率和主曲率,分析了在一个正弦周期中曲率的变化规律,为圆柱正弦活齿传动的接触强度计算奠定了基础;
4.根据活齿传动啮合副的相对运动对活齿的运动状态进行了分析;推导出共轭齿廓间的滑动计算公式,并考虑各齿形参数变化对滑动率的影响,对圆柱正弦活齿传动共轭齿廓间的磨损情况作了定性分析。
上一页
下一页


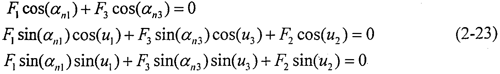




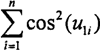 ,求解过程如下:
,求解过程如下: