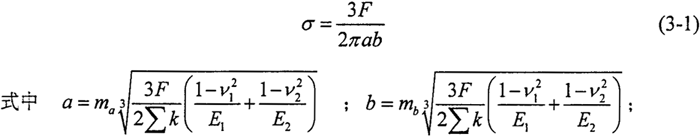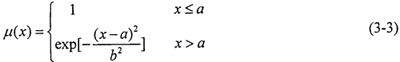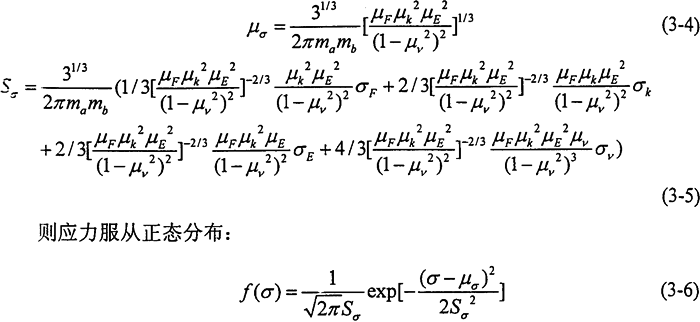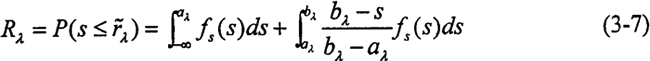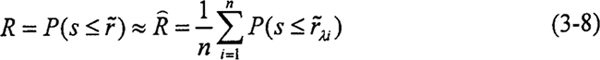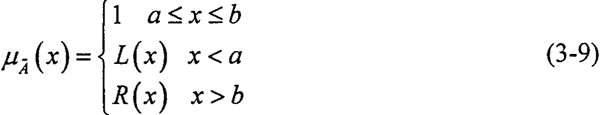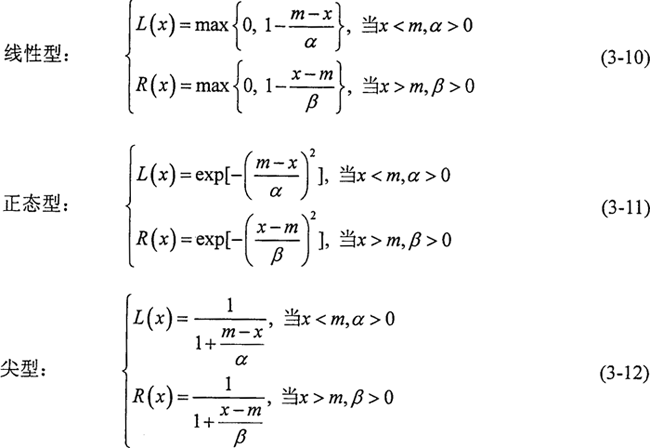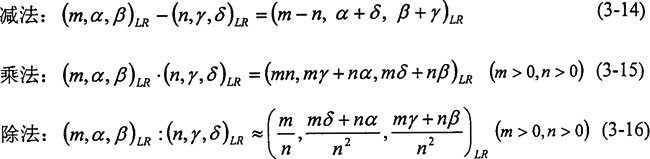第3章 圆柱正弦活齿减速器模糊可靠性的研究
3.1引言
圆柱正弦活齿减速器可以应用在航天机械、采油装置及机器人传动等复杂的工作环境中，其可靠性的好坏直接影响生产的效率和安全，为此，对它进行可靠性研究具有十分重要的意义。圆柱正弦活齿减速器的可靠性研究应包括以下两个方面：一方面是机械零部件本身的可靠度研究，即组成减速器系统的各个零部件完成所需功能的能力。另一方面是减速器乐统的可靠性研究。其中系统的可靠度还取决于系统中机械零部件组合的方式。
在圆柱正弦活齿减速器系统中，活齿与正弦滚道齿面的接触方式为点接触，则正弦滚道齿面与活齿的工作表面发生点蚀或胶合是该啮合副的主要失效形式，对其进行接触强度的可靠性研究，对提高齿面强度、降低失效概率具有非常重要的意义。接触强度的点蚀破坏是由于损伤积累引起性能下降最终导致故障的出现，系统从完好到失效是一个循序渐进的过程，其间呈现出亦此亦彼的模糊状态，因此在机械系统中随机性与模糊性是密切相关的，本章将模糊数学方法和随机方法结合起来，对圆柱正弦活齿传动的接触强度进行模糊可靠性分析，突破了常规设计方法中将应力、强度视为确定量而忽视其随机性和模糊性的局限性，使设计结果更加合理，更为真实。
在系统可靠性研究方法中，故障树分析（FTA）是一种用于复杂系统可靠性和安全性分析的有效方法，FTA是一种图形演绎方法，能通过对可能造成系统故障的多种因素（包括软件、硬件、环境、人为因素）进行分析，画出逻辑框图即故障树，从而确定系统故障原因的各种可能组合方式或其发生概率。本章在分析圆柱正弦活齿减速器系统结构及功能关系的基础上，建立圆柱正弦活齿减速器的故障树，确定了系统的最小割集。将模糊数学引入传统的故障树分析中，根据建立的故障树中各事件的逻辑关系，采用模糊数的运算法则及模糊算子AND和OR计算出系统以“输出轴不传递扭矩”为故障的模糊概率值。
为体现真实工况下减速器系统的可靠性情况，在建立故障树的基础上，基于Monte-Carlo方法对圆柱正弦活齿减速器进行可靠性的数字仿真。由此得到了系统故障的可靠度、失效概率及寿命分布等一系列可靠性指标，并通过对基本部件模式重要度的分析，找出系统薄弱环节，对改进和重新设计系统具有很大约启发性和指导性。
3.2圆柱正弦活齿传动副的接触强度模糊可靠性研究
在机械传动系统中，由于受到弹性模量、几何尺寸、载荷分配等因素的影响，各零件的工作应力均具有随机性，对此可用统计的方法将其视为随机变量来处理；另一方面，由于受到各种客观条件的限制，传动零件的接触强度等设计变量难以精确定量，存在亦此亦彼的状态，将这种变量处理为模糊变量，用模糊集合与隶属函数来描述。考虑到应力和强度作为随机变量和模糊变量，因此机诫传动系统的强度设计可按模糊可靠性设计方法进行墓它突破了常规设计方法中将应力、强度视为确定量而忽视其随机性和模糊性的局限性，使设计结果更加趋于合理，因此更为接近实际情况。
3.2.l接触应力计算
圆柱正弦活齿传动的啮合副在载荷作用下，活齿分别与主动轴的外滚道及壳体的内滚道接触，一般滚道半径取r′= (1.04-1.11)r,r为活齿半径。活齿与滚道的接触问题，可看作两自由曲面体的弹性接触问题，根据赫兹（Hertz）应力理沦，在外加总载荷F作用下两自由曲面弹性体的接触应力计算公式为
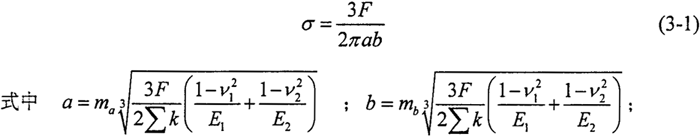
ma、mb——与椭圆偏心率有关的系数，可根据∑k及F（k）查表得到；
F（k）——主曲率函数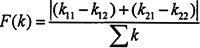
；
∑k——主曲率和∑k=k11+k12+k21+k22，（1/mm）；
k11、k12——活齿齿面的两个主曲率（1/mm）；
k21、k22——正弦滚道齿面的两个主曲率（l/mm）。
由于啮合副两接触面的材料相同，故选取弹性模量E1=E2=E，泊松比v1=v2=v。通过对圆柱正弦活齿传动进行受力分析可知，在正弦滚道的拐点附近，活齿与滚道间的接触力及接触应力均达到最大值，因此活齿与正弦滚道齿面的最大接触应力公式可写为
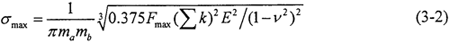
3.2.2接触强度的模糊可靠性研究
滚道齿面从完好状态到失效状态，其许用应力[σH]是一个渐进的衰减过程，为了更真实的反映[σH]的模糊性，本文采用降半正态分布的隶属函数来表示[σH]。降半正态分布的隶属函数为
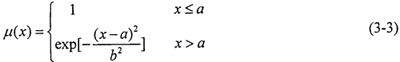
式中 u（x)- [σH]的隶属度；a、b为分布系数。
隶属函数曲线如图3-1。
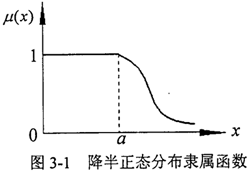
将F、∑k视为随机变量，并近似按“3σ”法求出其均值μF、μk与标准差SF、Sk，根据文献，弹性模量E、泊松比v均为随机变量，且近似服从正态分布，弹性模量的变异系数对钢而言不超过0.03，即弹性模量的标准差为6180MMPa，而泊松比的变异系数一般在2%-3%左右，则泊松比的标准差为0.009。按可靠度计算的一次二阶矩原理，将齿面接触应力的表达式在基本变量的平均值点处展开成泰勒级数，仅取级数的线性项，则可近似求得应力的均值μa与标准差Sσ分别为：
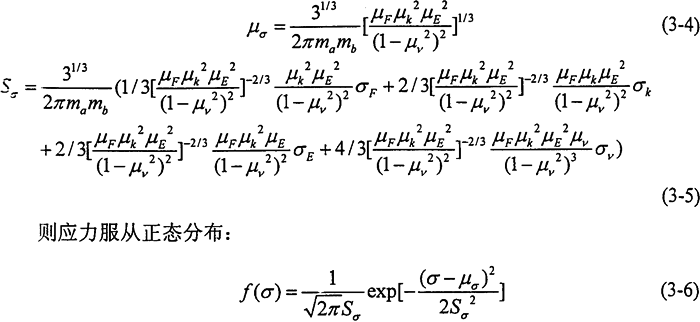
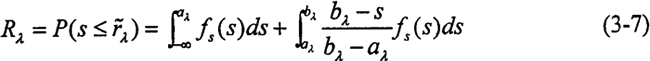
应用数字仿真法求出零件的可靠度R，即在（O,1）内产生均匀分布的随机数作为阈值λ1，并利用式（3-7）计算此时零件的可靠度Rλi，在仿真次数n足够大时，零件的可靠度可表示为：
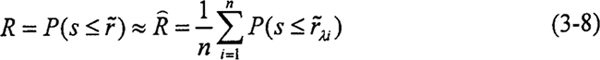
3.2.3圆柱正弦活齿传动接触强度的可靠性计算
圆柱正弦活齿减速器的结构和性能参数为Z1=1、Z3=4、A=4mm、r=4mm、输出轴扭矩T=20N.m，其主要零件如活齿、主动轴、导架及壳体的材料选用GCr15，淬火后硬度为HRC=58～62，由于圆柱正弦活齿传动采用二硫化铝作为固体润滑剂，考虑到二硫化钥的最大抗压强度为2800MPa，根据模糊数学中确定容差的扩增系数法，该传动的主要零件的许用接触应力选为2450～2800MPa。将上述参数代入式（3-4）、（3-5）中，求得主动轴正弦滚道与壳体正弦滚道接触应力的均值和方差，再利用式（3-8)，仿真次数n选取2000次，计算圆柱正弦活齿传动正弦滚道的接触强度的可靠度见表3-1。
表3-1滚道接触强度的可靠度
| |
均值（MPa） |
方差（MPa） |
可靠度 |
| 主动轴 |
2322.9 |
192.12 |
0.9744 |
| 壳体 |
2325.7 |
172.31 |
0.9781 |
| 导架 |
2284.4 |
300.51 |
0.9145 |
由表3-1可知，导架的接触强度可靠度最低，是整个系统可靠性的薄弱环节。因此，在结构设计中，应尽量提高导架的接触强度可靠度，以改善圆柱正弦活齿减速器系统的可靠性。
3.3减速器系统的模糊可靠性研究
故障树分析是分析系统可靠性的一种方法，它根据系统的结构或功能关系，利用图形演绎的方法把故障传递的逻辑关系表达出来，对此可逐级分析系统故障发生的原因，对系统进行故障概率的计算，以便采取相应的措施，来提高系统的可靠性。
3.3.1减速器系统故障树的建立
根据圆柱正弦活齿减速器的结构及其实现的功能，采用自上而下的方法建立故障树，首先选取“输出轴不能传递扭矩”作为顶事件，然后找出导致顶事件的所有可能直接原因，作为第一级中间事件，用相应的事件符号将其表达出来，并用适合的逻辑门符号表示中间事件与顶事件之间的逻辑关系。依此类推，逐级向下发展，直到找出引起系统故障的全部原因，作为底事件，由此建立了圆柱正弦活齿减速器的故障树（图3-2）。
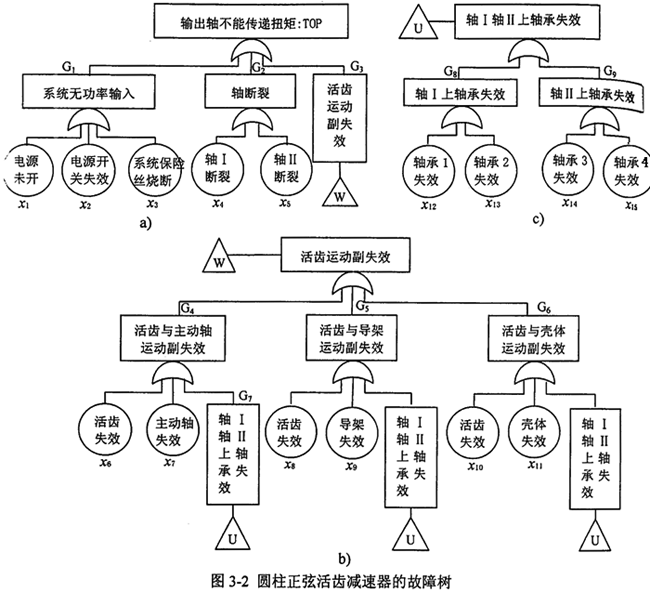
3.3.2减速器系统故障树的分析
故障树的分析包括定性分析和定量分析。定性分析的主要任务是寻找故障树的全部最小割集和最小路集，一个最小割集代表系统的一种失效模式，一个最小路集代表系统一种正常模式。通过对最小割集和最小路集的研究，可以发现系统的薄弱环节和最关键的部分，以便针对具体对象采取相应的措施，有利于维持和提高系统的功能。本本文只讨论系统的失效模式，故须寻找出故障树的最小割集即可。根据对圆柱正弦活齿减速器的故障树分析得出最小割集为{xi}，i=1，2…，15。他们分别对应系统15种失效模式。
故障树的定量分析是运用故障树中建立的逻辑关系，根据底事件发生的概率推导出顶事件发生的概率，从而对系统的可靠性、安全性作出评价。故障树中各种事件间的因果关系用各种“门”来描述，并且大多可以等效为逻辑“与门”和“或门”。根据“与门”和“或门”所表示的事件关系，并假设各个事件互相独立，根据表3-2即可计算活齿减速器中各中间事件和顶事件的发生概率。
表中 P（T）——顶事件发生概率；
P（xi）——底事件发生概率，i=1，2，…，15；
P（Gi）——中间事件发生概率。i=1，2，…，9。
3.3.3圆柱正弦活齿减速器的模糊故障树分析
故障树分析重要的环节是获得事件发生的概率。传统的故障树分析以布尔代数为基础，把事件发生的概率处理成精确值，然而由于实际工作环境的模糊性及数据的不精确，会对确定事件的概率产生影响，因此难以用一精确值来表示事件发生的概率。在传统故障树分析中，当事件发生的概率难以精确赋值时，可对故障树进行模糊分析。
3.3.3.1模糊分析的理论基础 在故障树的模糊分析中，采用模糊数来描述事件发兰的概率。模糊数是由概念上的模糊性或各种模糊因素的影响而造成定量处理时的不确定性。以模糊数描述概率值，带有人的主观性，强调了人在系统可靠性分析与评价中的重要性。因此，故障树的模糊分析不仅可减少获取事件发生概率精确值的难度，而且能结合工程中的实际经验和判断构造模糊数为隶属函数，较准确地把它们描述出来，并在一定程度上允许存在描述误差，具有较大的灵活性和适应性。
定义1 模糊数
为实数域R上的正规凸模糊集，其隶属函数满足
（1）maxμ（x）=1 x∈R
（2）μ（x）是逐段连续的
定义2 若模糊数的隶属函数满足
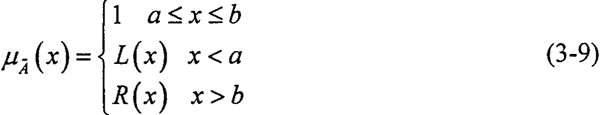
则称模糊数为L-R型模糊数，L(x）、R(x）称为模糊数的左、右参照函数。工程中，模糊数隶属度为1的数通常只有一点，因此模糊数可表示=（m，a，β）。其中m是模糊数的均值，对应隶属度为l的数；a、β分别为左、右分布；当a、β为零时，不是模糊数。分布a、β越大，越模糊。
常用的L-R参照函数为：
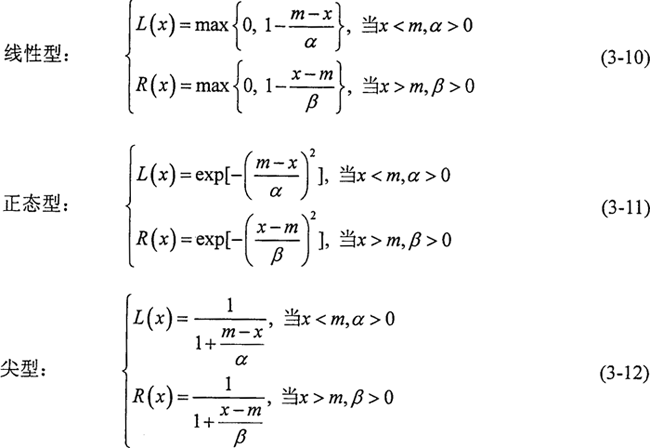
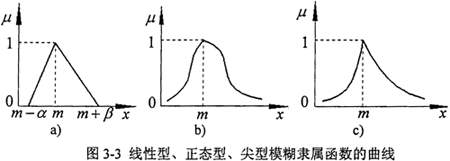
线性型参照函数在“完全属于”和“完全不属于”之间的中介状态是线性变化的（图3-3a），当x≤m-α和x≥m+β时，μ=0，说明在（m-α，m+β）区间之外的数值完全不属于该模数数。而其他两种类型的隶属函数曲线两端延伸至无穷远（图3-3b，c）说明整个数轴上的任何数总在一定程度上隶属于该模糊数。在选择参照函数时，除非有绝对的把握认为该事件发生的概率在某个范围之内而选择线性参照函数，否则，以选取正态型或尖型为好。
模糊数的代数运算法则如下：
加法：（m，α，β）LR+（m+n，α+γ，β+δ）LR （3-13）
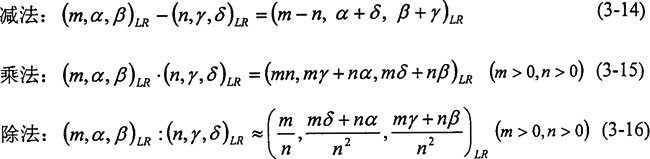
式（3-15）、（3-16）是近似的，严格地说，两个L-R型模糊数葙乘或相除，其结果不再是L-R型模糊数。
3.3.3.2模糊算子AND和OR模糊算子AND和OR反映了“与门”和“或门”的模糊逻辑运算。对于“与门”，其模糊算子为：
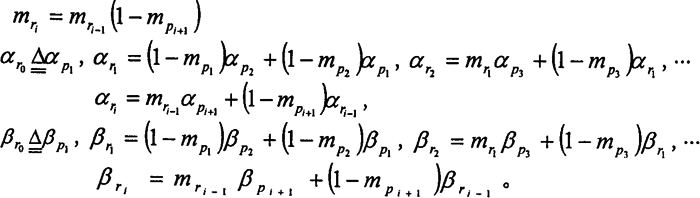
3.3.3.3圆柱正弦活齿减速器故障树分析 根据圆柱正弦活齿减速器故障树，用模糊算子ACD和OR描述基本事件间的逻辑关系，生成值值函数的模糊形式及用模糊算子表达的形式见表3-3。
上一页
下一页
