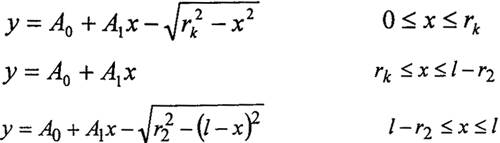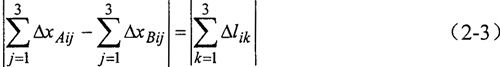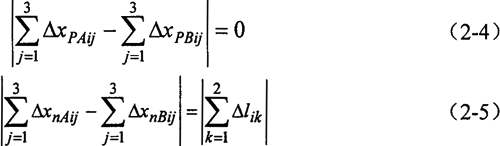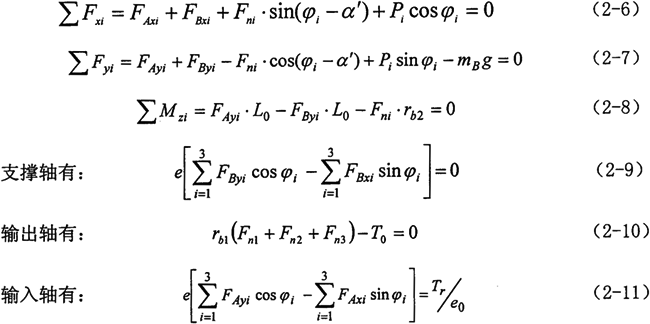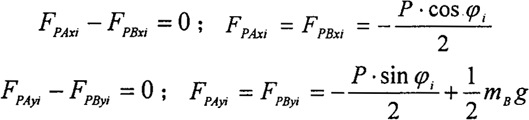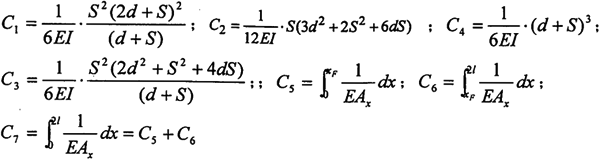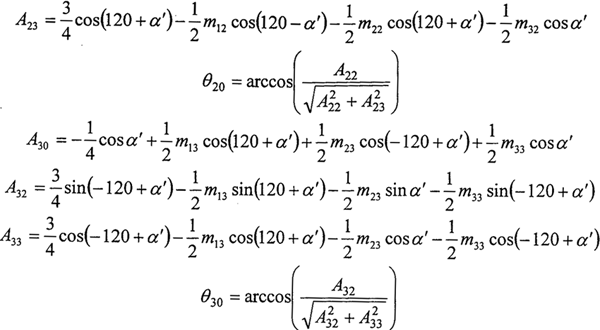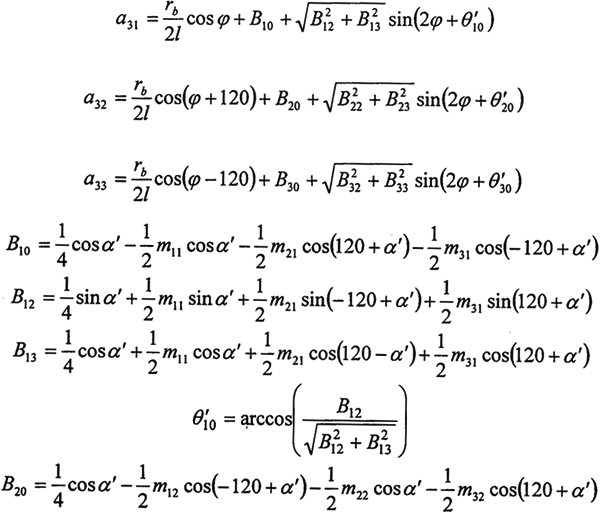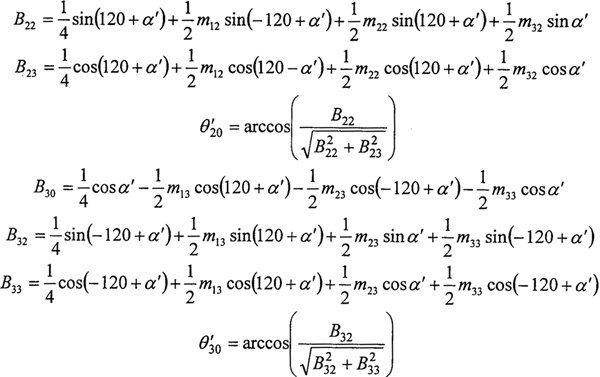第2章 完全平衡双轴输入三环减速器的动力学研究

2.1 引言

三环减速器的研究起步较晚，产品研制的时间较短，尽管一些厂家和科研院所对其进行过一些研究和试验，取得了一些成果，但是，生产中出现的诸如：振动大、温升高及转臂轴承使用寿命短等诸多问题还未得到有效地解决，这严重影响了三环减速器的推广使用。目前，三环减速器的受力分析、效率计算和振动及发热等问题的研究表明，采用双轴输入及对称型三环传动形式可减少三环减速器的振动，进而提高三环减速器的使用寿命。受力分析是三环减速器设计的基础，针对目前三环减速器变形协调条件处理过程简单化、影响计算精度的问题，本章改进了考虑环板形状和受力实际的变形协调条件，并对三环减速器的受力进行了分析；依据连杆机构平衡理论，提出了完全平衡双轴输入三环减速器设计的理论依据；曲柄轴和输出轴的支撑轴承处的受力分析揭示出惯性力和惯性力矩、啮合力对基本型和完全平衡型三环减速器振动的影响；最后，本章还对完全平衡三环减速器的振动问题进行了研究，结果表明：完全平衡双轴输入式三环减速器有着优越的机械性能。

2.2 基本型三环减速器的受力分析

2.2.1 结构组成及基本原理

现有的理论研究、试验分析和产品的应用都证明，对称型三环减速器较偏置型有着优越的机械性能，作为笔者设计的完全平衡双轴输入式三环减速器的对比样机，本章选的是对称型三环减速器。对称型三环减速器的基本结构如图2-1所示，其输入轴和支撑轴对称布置在输出轴的两侧。其输入轴通过三片完全相同且互成120°的偏心套及相匹配的滚动轴承与内齿环板构成三个平行双曲柄机构，传动环板在输入轴的驱动下作轨迹为圆的平动，传动环板上的内齿圈与输出轴上的外齿轮相啮合，实现了输出轴的低速输出。每一片内齿环板均为一个平行双曲柄机构，三块环板同时驱动输出轴齿轮。理论上，任一瞬时各环板所受的载荷大小相等，由于不可避免的制造安装误差及传动过程中的弹性变形，使实际工作时各环板所受载荷并不相同，也就是各传动环板之间的载荷分配不够均匀。这种现象严重影响三环减速器性能的发挥，并产生振动和噪音，严重时，会导致异常工作情况甚至出现事故。现有三环减速器采用哪图2-2所示三相平行双曲柄机构的目的主要是克服机构死点和使惯性力平衡。

2.2.2 惯性力和惯性力矩

设内齿环板的质量为m_B，转臂偏心曲柄的质量（含转臂轴承）为m_H，环板的质心在O点，两转臂偏心轴的瞬时质心分别在O₁，O₂点，转臂转速为n_H,因内齿环板作平动，则其转速n_b为零，因而，质心以n_H转速绕O₁，O₂转动，r_b2为内齿轮的基圆半径，r_b1为外齿轮的基圆半径，α为压力角，α′为啮合角，e₀为偏心距，m为内或外齿轮的模数，Z₁，Z₂为内啮合的内、外齿轮的齿数。每片内齿环板的惯性力为：

P_i=m_Bω_H²e₀=[mπ²(Z₂-Z₁)m_内/1800]·(cosα/cosα′)·n_H²           (2-1)

每个转臂偏心轴（曲柄）的惯性力为：

P_Hi=m_Hω_H²e₀=[mπ²(Z₂-Z₁)m_H/1800]·(cosα/cosα′)·n_H²           (2-2)

这里，i=1，2，3

2.2.3 三环减速器的变形协调条件

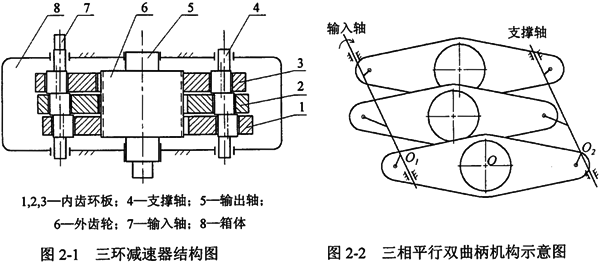
三环减速机运动属静不定问题，用一般平面刚体力学方法无法完全求出机构的作用力，影响到三环减速器设计和传动性能的改进。为此需要考虑各构件的变形，建立能充分反映三环减速器实际受力的变形协调条件作为补充方程。三环减速机传动机构是双曲柄连杆机构，曲柄的旋转半径是偏心轴的偏心距，曲柄布置在由支撑轴承支承的偏心轴上，环板是双曲柄机构的连杆，传动过程中的主要变形有各构件的接触变形、轴的扭转弯曲变形、环板的拉压变形等等。根据位移变形分析可知，轴的弯曲变形和环板的拉压变形是主要的变形形式。对于笔者设计的如图2-3所示的环板，设A为输入轴，B为输出轴。为了计算上的方便，以前将其简化为等截面杆处理。实际上，由于有效截面的最大面积是最小截面面积的5倍多，这种简单地处理和实际有较大的差别。环板受拉压变形时的有效拉压面积的形状如图2-4所示（单位：mm）。

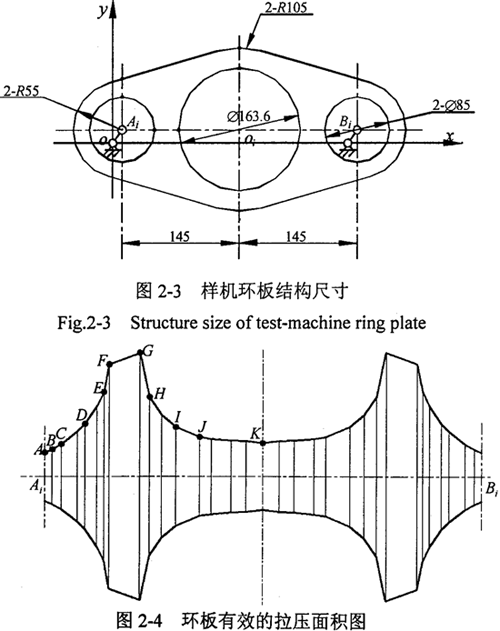
其实际的拉压截面曲线由下面的方程分段给出（长度单位：mm）：

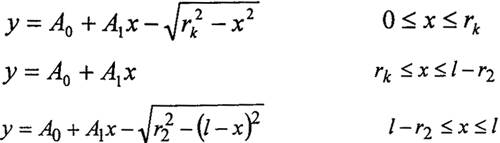
式中    A₀=58.594；    A₁=0.36736；    r_k=42.5；    r₂=81.8；    l=145

由方程绘出这际拉压截面曲线图可看出，工程上所用的实际环板的结构形状和方程较为复杂，对其拉压变形量难以直接积分求解。但简单地将有效截面的最大面积与最小截面面积相差5倍的环板的有效拉压面积处理成等截面圆柱则误差较大。由于啮合力连续作用在曲线方程较为复杂的中间各位置点，若根据实际形状（方程）加以积分求解在数学上又较为困难。对于此类问题，采用工程上实用的最小二乘法将实际曲线拟合成分段斜直线组成的近似函数，则很有效，这样做，既可保证精度，又可用简单的积分公式编程直接求解。

尽管转臂轴承两端的截面尺寸也不大，但由于轴承外表面与环板接触的断面积较大，且轴承的刚度较大，故此处产生的挤压变形与轴的弯曲变形相比较小，可忽略。

由于环板的结构是对称的，对其中的1/4进行研究就可以了。根据环板的实际，将图形分成10段。每段的拟合方程均为：

y_i=A_0i＋A_1ix_i

每段方程中的系数如表2-1所示：

表2-1 方程的系数

	AB	BC	CD	DE	EF	FG	GH	HI	IJ	JK
A0	16.09	15.43	11.96	-9.00	-251.97	58.86	365.5	130.3	68.95	34.36
A1	0.43	0.56	0.86	1.65	5.19	0.36	-4.61	-1.13	-0.42	-0.083

设任一环板在x方向上分别受到F_Aix、F_Bix、啮合力F_ni，水平分力和惯性力P_i，水平分力的拉伸或压缩作用；如图2-5所示的输入轴上任一环板两环板支点A_i（B_i）在x方向的挠度△x为偏心轴颈上环板轴承x方向的作用力F_A1x，F_A2x，F_A3x（F_B1x，F_B2x，F_B3x）在A_i（B_i）点作用的挠度△x_{Ai(Bi）的叠加。以S代表输入轴支承轴承与相邻环板之间的距离，d表示相邻环板之间的距离。则考虑输入轴的弯曲变形和环板拉压变形三环减速机变形协调条件为：在外力作用下，任一环板处两曲柄轴在x方向的挠度的差等于该环板在x方向的总变形。用公式2-3表示。}

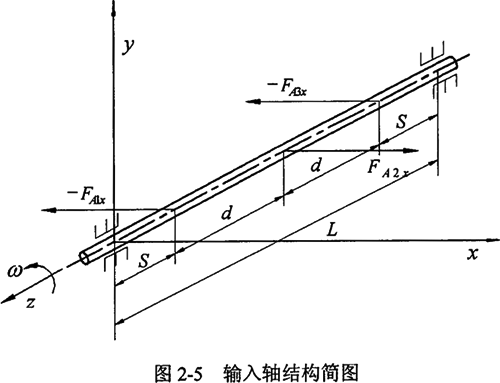
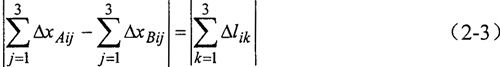
实际运算中，采用下面的形式更为有效，求解也更为方便。（2-4）式的证明将在下一节的受力分析中给出证明。

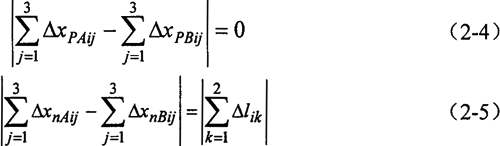
式中 △x_Aij，△x_PAij，△x_nAij，——在一输入轴上环板处A_i点的由于力F_Ajx，F_PAjx，F_nAjx作用的挠度（j=1，2，3）；这里，F_Ajx=F_PAjx+F_nAjx。

△x_Bij, △x_PBij，△x_nBij——另一输入轴上环板处B_i点的由于力F_Bjx，F_PBjx，F_nBjx作用的挠度(j=1，2，3)；这里F_Bjx=F_PBjx+F_nBjx。

△l_ik——对应于A_iB_i的一块环板在x方向由啮合力水平分力作用下产生的拉压变形（k=1，2）。

2.2.4 三环减速器的受力分析

1.转臂轴承上的作用力分析 内齿环板受力见图2-6所示。

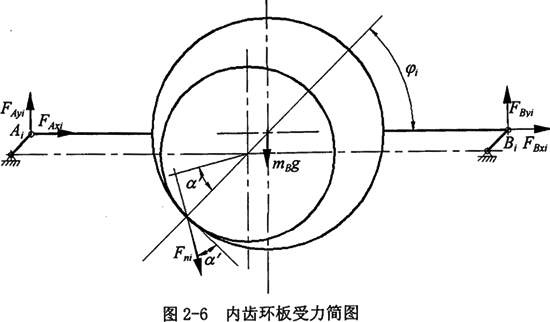
设两转臂偏心轴的瞬时几何中心分别在A和B点，L₀为内齿环板中心与转臂轴承中心之间的距离，F_n为外齿轮作用给内齿板的力（切于基圆，指向啮合点）。转臂轴承上A_i和B_i的作用力为F_Ai（分解为F_Axi和F_Ayi）和F_Bi（分解为F_Bxi和F_Byi），由力（力矩）平衡方程，对于第i块环板可列如下方程：

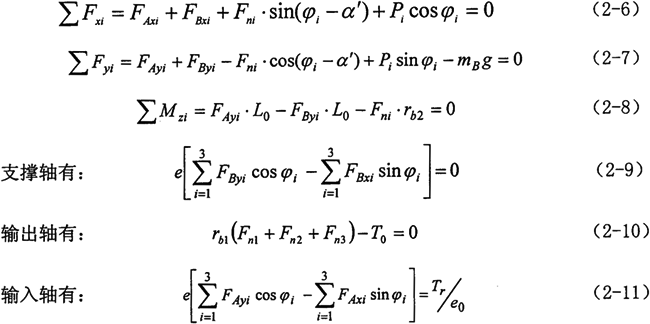
由于方程数为12个，而方程中的未知量的总数为15个，属静不定问题。需建立变形协调方程作为补充方程，方程才能得以求解。

对于作用在任意一块环板的惯性力和啮合力来说，可根据力的叠加原理，将惯性力和啮合力分别作用在A_i和B_i的力求出后，再将其叠加便可得到环板点A_i和B_i的作用力。由力学原理和变形协调方程有：

仅考虑环板上作用的惯性力和重力。

第i块环板可列如下方程：

∑F_Pxi=F_PAxi+F_PBxi+P_icosφ_i=0            (2-12)

∑F_Pyi=F_PAyi+F_PByi+P_isinφ_i-m_Bg=0          (2-13)

∑M_Pzi=F_PByi·L₀-F_PAyi·L₀=0            (2-14)

变形协调条件方程（假设环板的变形之和不为零）：

|C₁(F_PAx1-F_PBx1)+C₂(F_PAx2-F_PBx2)+C₃(F_PAx3-F_PBx3)|=|F_PAx1C₅-F_PBx1C₆|      (2-15)

|C₂(F_PAx1-F_PBx1)+C₄(F_PAx2-F_PBx2)+C₂(F_PAx3-F_PBx3)|=|F_PAx2C₅-F_PBx2C₆|      (2-16)

|C₃(F_PAx1-F_PBx1)+C₂(F_PAx2-F_PBx2)+C₁(F_PAx3-F_PBx3)|=|F_PAx3C₅-F_PBx3C₆|      (2-17)

由于环板的惯性力作用在环板的中心，而环板的结构又是对称的，故有C₅=C₆，代入上面方程并求解有：

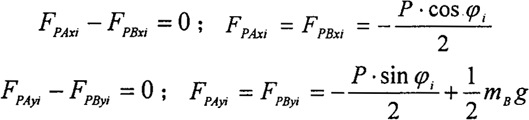
由于上式和C5=C6知，惯性力作用在环板上的拉压变形之和为零，方程（2-4）式得证。

仅考虑环板上作用的啮合力。

∑F_nxi=F_nAxi+F_nBxi-F_ni·sin(φ_i-α′)=0               (2-18)

∑F_nyi=F_nAyi+F_nByi-F_ni·cos(φ_i-α′)=0               (2-19)

∑F_nzi=F_nAyi·L₀-F_nByi·L₀-F_nir_b=0               (2-20)

变形协调条件方程：

|C₁(F_nAx1-F_nBx1)+C₂(F_nAx2-F_nBx2)+C₃(F_nAx3-F_nBx3)|=|F_nAx1C₅-F_nBx1C₆|             (2-21)

|C₂(F_nAx1-F_nBx1)+C₄(F_nAx2-F_nBx2)+C₂(F_nAx3-F_nBx3)|=|F_nAx2C₅-F_nBx2C₆|             (2-22)

|C₃(F_nAx1-F_nBx1)+C₂(F_nAx2-F_nBx2)+C₁(F_nAx3-F_nBx3)|=|F_nAx3C₅-F_nBx3C₆|             (2-23)

式中

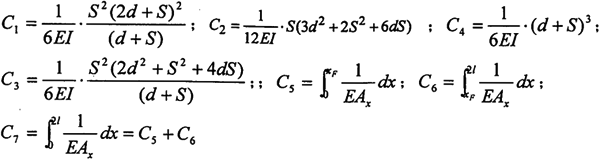
式中 E——环板材料的弹性模量，本文取为2.06×10¹¹N/m²；

I——轴的截面对中性轴的惯矩，。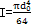

x_F=l-rcosφ_i

将F_nBxi=-F_nAxi+F_nxi代入式（2-21）～（2-23）中，求解得：

F_nAX1=m₁₁F_n1x+m₁₂F_n2x+m₁₃F_n3x

F_nAX2=m₂₁F_n1x+m₂₂F_n2x+m₂₃F_n3x

F_nAX3=m₃₁F_n1x+m₃₂F_n2x+m₃₃F_n3x

式中

由此可得到各个环板转臂轴承所受的力。

将以上关系代入支撑轴方程（2-9），并整理有：

a₁₁F_n1+a₁₂F_n2+a₁₃F_n3=0                    (2-24)

式中

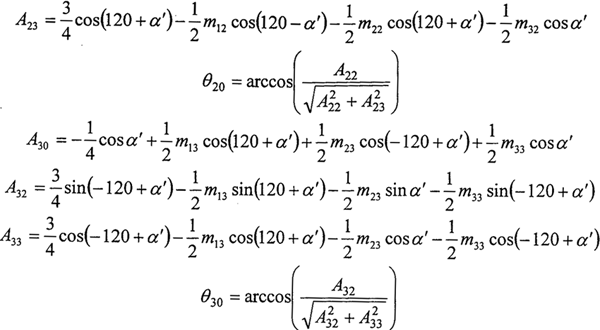
代入输入轴方程（2-11），并整理有：

a₃₁F_n1+a₃₂F_n2+a₃₃F_n3=T_r/e₀               (2-25)

式中

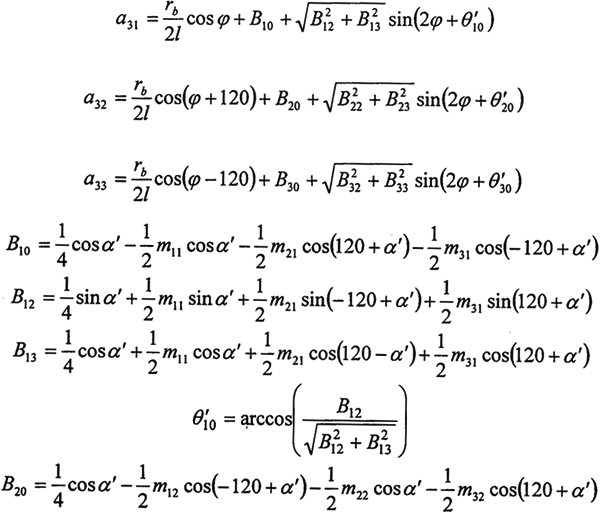
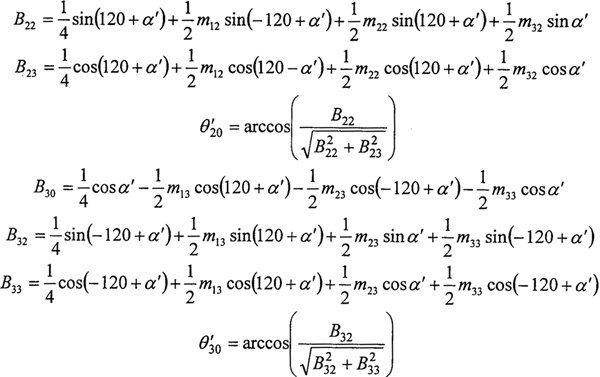
求解曲柄轴（2-24）、（2-25）和输出轴（2-10）组成的关于啮合力的方程组，可解得：

由上式可看出，任意时刻各环板上作用的啮合力是不相等的，且是与转角、环板和曲柄轴结构尺寸、压力角以及偏心尺寸有关的复杂函数，假设各啮合力相等或者是成一简单的函数关系都是与实际严格不符的。若需要用简洁的函数关系加以描述，应首先利用上式求出输出轴旋转一周时的数个啮合力的表达式，这里不作详细的讨论。

上一页

下一页