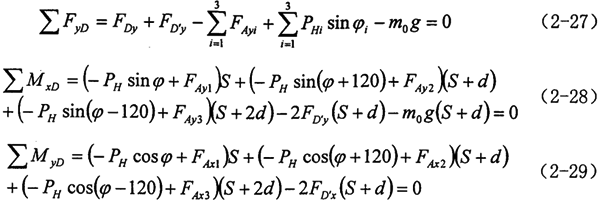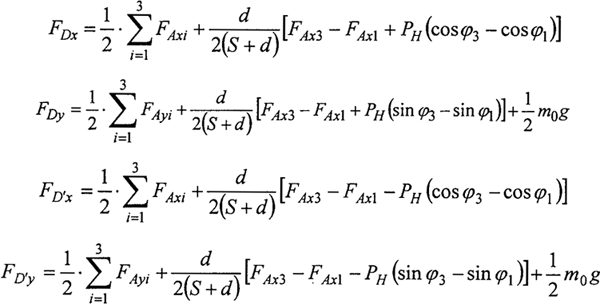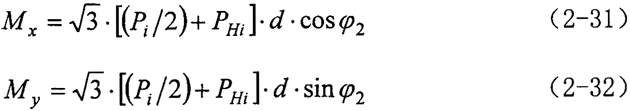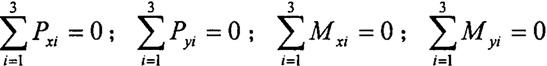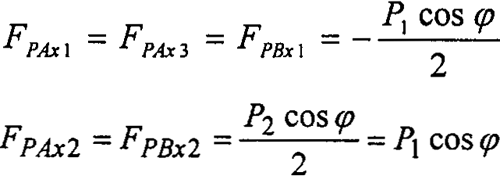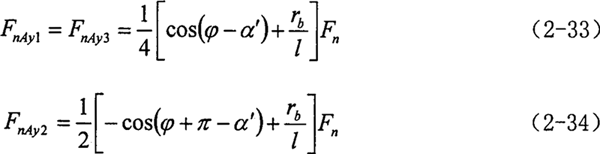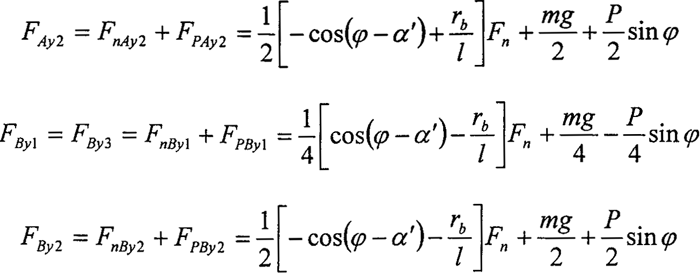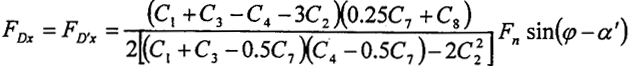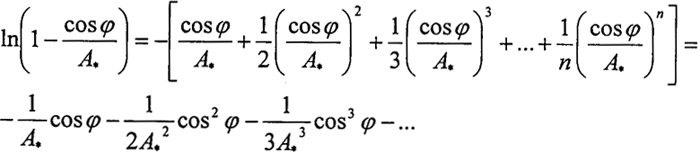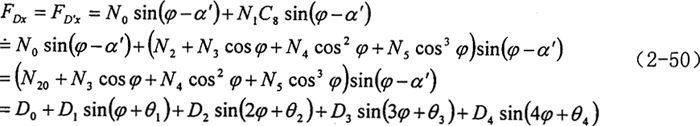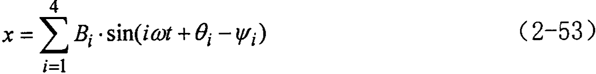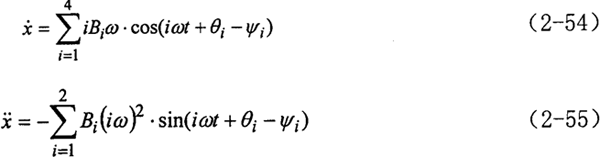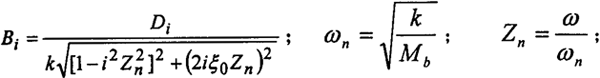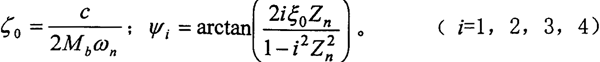2.曲柄轴支撑轴承的作用力分析 根据力学原理,对于输入同可得到下列方程式:
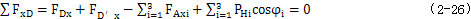
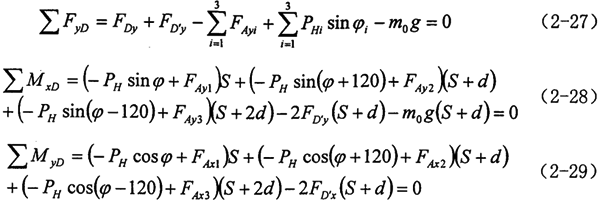
解方程,有:
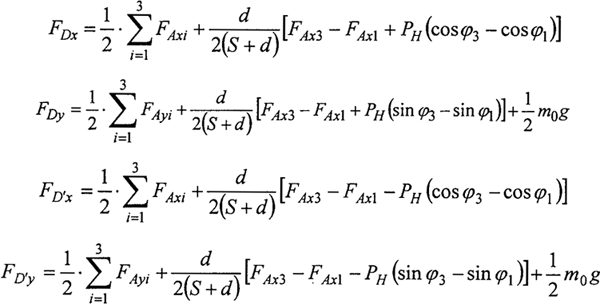
将上述方程中的A和D′换成B和G′,以及rb/l换成-rb/l便得到了支承轴的支撑力。
同理,列出输出轴的力和力矩方程,并求解有如下结果:

由方程的解可看出,不论是曲柄轴还是输出轴,其支撑轴承既受到惯性力(力矩)的作用,还受到啮合力(力矩)的作用。由公式可看出,该三环减速器环板的布置型式,即使各环板的啮合力相等,啮合力作用在各轴的两侧支撑轴承处的作用力也是不等的。由于各环板的啮合力是不相等的,且各啮合力是与转角和环板结构尺寸等参数有关的的复杂函数,所以各轴的两侧支撑轴承受到较大的由啮合力(力矩)和惯性力(力矩)引起的周期激进力的作用,这是三环减速器振动大的原因。对于支承轴来说,各环板在其上作用的转矩和为零,但每相双曲柄机构在其上的作用转矩是不断变化的,在一个周期中,既受到正转矩的作用,也受到反方向转矩的作用,这种转矩的波动将通过曲柄轴作用到安装在箱体上的支撑轴承上,引起减速器的振动。
2.3 设计的理论依据及设计参数的确定
2.3.1 惯性力和惯性力矩的计算
1.惯性力的作用由上节转臂轴承的受力分析知,环板惯性力作用在两曲柄轴每一环板上的转臂轴承的惯性力各为环板惯性力的l/2。
每一曲柄和环板的惯性力作用在曲柄转动中心的惯性力为:(PBi/2)+PHi
由于在基本型三环减速器曲柄轴上作用的三个惯性力大小相等,方向成120°,构成了一个封闭的力三角形。故,曲柄轴上的惯性力之和为零。
所以,作用在偏心轴上的惯性力的矢量和为零:

上式表明,该基本型三环减速器传动机构是静平衡的。
2.惯性力矩的作用 以中间环板在曲柄轴的作用点为坐标原点,以曲柄轴方向为动轴x′方向(与x′方向相垂直方向为y′)进行分析,由于中间环板的惯性力通过坐标原点,不产生惯性力矩。由于两侧环板相对于中间环板对称布置,两环板在x′方向的惯性力分力所产生的惯性力矩之和(对y′轴取矩)为零,而两侧环板在方向惯性力分力大小相等方向相反,其产生的相对于x′轴的惯性力矩为:
Mx′=2·[(Pi/2)+PHi]sin(π/3)·d
则相对于x和y轴的惯性力偶矩分别为
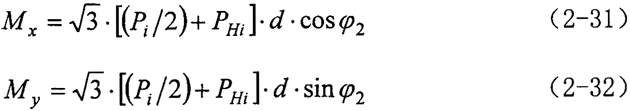
这表明:对称型三环减速器的惯性力是平衡的,但惯性力矩则是不平衡的。
2.3.2 设计的理论依据及设计参数的确定
三环传动的内齿环板作曲线平动,每片内齿环板都相当于一个平行双曲柄机构的连杆,环板上的任意点的轨迹均为以偏心轴的偏心距为半径的圆。为此,要求环板除轴向厚度外的其它各结构尺寸均相同。
对于对称型三环减速器,设环板及与其对应的曲柄的质量为mB, mHi(包含转臂轴承的质量),相应的板厚为bi,每相双曲柄机构的质心在环板的中心,并记单位厚度环板的质量为mb。(综合考虑了环板和曲柄的质量)。靠近输入侧的环板编号为1,其曲柄转角为φ;中间环板为2,其对应的曲柄转角为φ+θ01;另一块为3,其对应的曲柄转角为φ+θ02。根据平面连杆机构的惯性力和惯性力矩的完全平衡理论,有下列关系式:
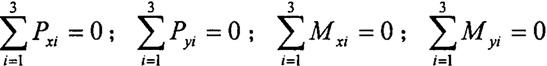
展开有:
mbb1ωH2e0cosφ+mbb2ωH2e0cos(φ+θ01)+mbb3ωH2e0cos(φ+θ02)=0
mbb1ωH2e0sinφ+mbb2ωH2e0sin(φ+θ01)+mbb3ωH2e0sin(φ+θ02)=0
mbb1ωH2e0Ssinφ+mbb2ωH2e0(S+d)sin(φ+θ01)+mbb3ωH2e0(S+2d)sin(φ+θ02)=0
mbb1ωH2e0Scosφ+mbb2ωH2e0(S+d)cos(φ+θ01)+mbb3ωH2e0(S+2d)cos(φ+θ02)=0
化简上式,有:
b1cosφ+b2cos(φ+θ01)+b3cos(φ+θ02)=0
b1sinφ+b2sin(φ+θ01)+b3sin(φ+θ02)=0
b2sin(φ+θ01)+2b3sin(φ+θ02)=0
b2cos(φ+θ01)+2b3cos(φ+θ02)=0
进一步化简,有:
b1sinφ-b3sin(φ+θ02)=0
b1cosφ-b3cos(φ+θ02)=0
求解上式,有sinθ02=0,即:θ02=0或π,代入方程检验知,只有θ02=0是方程的解。
将θ02=0回代。可方便得到:b1=b3;θ01=π和b2=2b3。
结果θ02=0,θ01=π, b1=b3和b2=2b3表明:惯性力和惯性力矩的完全平衡的三环减速器的两则环板完全相同,且偏心相位差为零;中间环板的厚度为侧面环板厚度的两部,且与侧面环板成偏心相位差为180°的布置。
该结果是我们提出的完全平衡三环减速器结构的理论基础。
2.4 完全平衡双轴输入三环减速器的弯曲振动分析
2.4.1 结构及工作原理
完全平衡双轴输入式三环式减速器如图2-7所示。其工作原理为:三环式减速器的曲柄轴在动力的驱动下同步旋转,传动环板上的内齿圈与输出轴上的外齿轮相互啮合,形成了大传动比,从而实现了减速及动力传递。双轴同步输入可以克服传动机构的死点问题。

2.4.2 新型三环减速器的受力分析
1.转臂轴承上的作用力 由于双轴输入式完全平衡三环减速器的环板结构与对称型三环减速器是一样的,仅由原来的单轴输入改为双轴同步输入,原来环板之间120°相位差布置改为现在的两侧环板同相位,与中间环板成180°相位差布置,因而其受力分析过程和第i块传动环板的力(力矩)平衡方程和变形协调方程也与对称型三环减速器一样。只是双轴输入式完全平衡三环减速器的啮合力由原理对称型三环减速器复杂的函数关系变成了常数。其值为:
Fn=T0/(2rb)
对形成的惯性力方程和变形协调条件方程联合进行求解,可方便的得出:
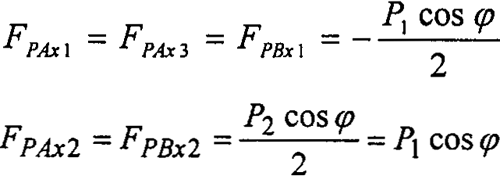
由于啮合点位置变化,下面求任意时刻啮合力作用在转臂轴承上的力。
将双轴输入的啮合力代入啮合力作用时的平衡方程和变形协调条件方程,并考虑环板1和环板3同相位,即:C61=C63,求解有:
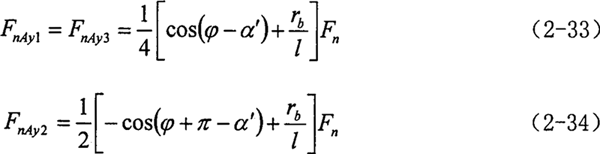

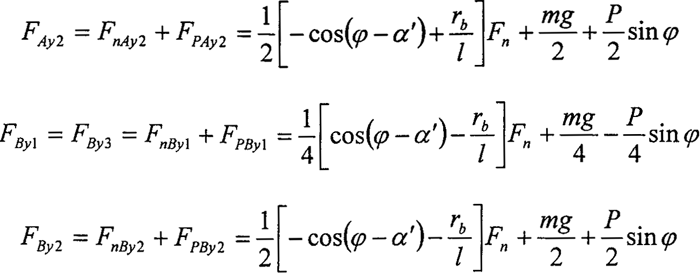
由此根据双轴输入工况时的力(力矩)平衡方程和变形协调方程便求得了第i块传动环板转臂轴承A及B处的所有反力。
输入轴转臂轴的受力图2-8和2-9所示。
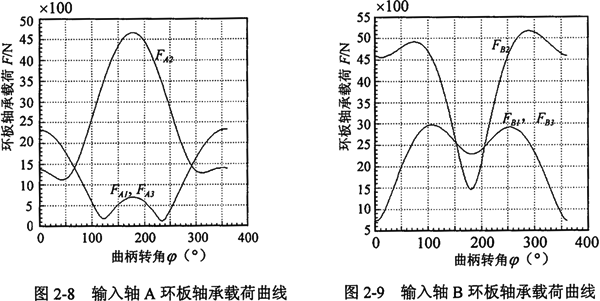
由环板轴承的受力曲线可看出,两输入轴环板轴承受力是不同的,其最大值也略有差别。
2.支撑轴承的作用力 根据力学原理,对于曲柄轴DD′列出力和力矩方程并求解有(忽略带轮上所受的力):
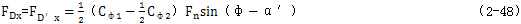
由于三环减速器的中间环板与两侧环板成180°布置,若令: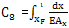
由:C61=0.5C7-C8;C62=0.5C7+C8,代入式(2-48),并整理有:
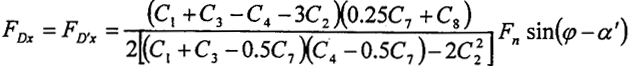
写成:
FDx=FD′x=N0sin(φ-α′)+N1C8sin(φ-α′) (2-49)
由于啮合点在不断的变化,也就是说C8关于转角的函数。

按幂级数展开有:
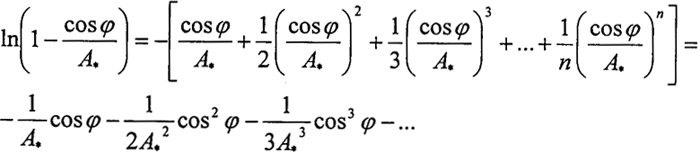
这里:A*=-A01/A11(l-rb)
取前三项足可以保证精度。将上式代入(2-49),并整理有:
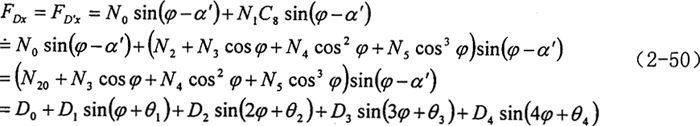
式中


两输入轴的支撑轴承D和G的受力情况如图2-10和2-11所示。
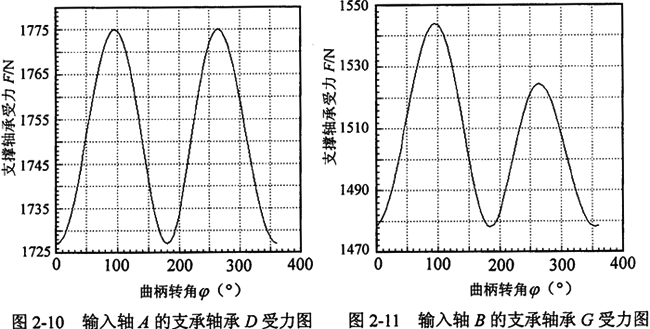
将上述方程中的A和D′换成B和G′,便得到了另一根曲柄轴的力和力矩方程。进而得到另一曲柄轴的支撑轴承的受力。
同理,列出并求解输出轴的力和力矩方程有如下结果:
FEy=FE′y=G/2
FEx=FE′x=0
式中 G——输出轴的重力。
此式表明,完全平衡双轴输入式三环减速器啮合力对输出轴是完全平衡。
24.3 三环减速器的振动分析
实际上,在工作过程中,惯性力和啮合力在轴的的作用点的变形量是不等的,即使是在惯性力平衡,各环板单位宽度上的啮合力相等的条件下,力作用在曲柄轴处的挠度也是不同的。如:输入轴的中间环板处x方向受力2,两侧各环板x方向受力各为-P,由力学原理,两侧环板处在曲柄轴x方向的挠度为:xz=0.6671 ,而中间环板在曲柄轴x方向的挠度为: xz=1.1603
,而中间环板在曲柄轴x方向的挠度为: xz=1.1603 ,约为侧面挠度的1.74 倍。若考虑其影响,整机的的惯性力和费性力矩也是不平衡的。由于各环板的载荷分布不均,啮合力的影响则更大。
,约为侧面挠度的1.74 倍。若考虑其影响,整机的的惯性力和费性力矩也是不平衡的。由于各环板的载荷分布不均,啮合力的影响则更大。
以曲柄轴DD′的D点为例研究其曲柄轴支撑轴承的受力后的振动。以x方向为例。
根据振动理论,可得到系统的运动方程为:

式中 Mb——曲柄轴质量的一半;C——轴承阻尼系数;k——轴承刚度。
式中的常数项,只对系统的静变形的位置有影响,而不会对系统在静平衡位置近旁振动的规律产生影响。因此,D0产生的自由衰减运动渐渐消失。
这是周期性激励引起的受迫振动方程。在激振动力作用下的位移响应,即:方程的稳态解(以固频率为频率的振动经过一段时间后将消失,不考虑)为:
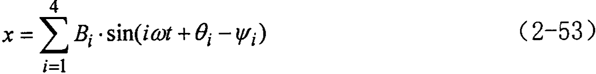
将有关参数代入上式便可获得系统的位移响应曲线。
对公式(2-53)求一阶导数和二阶导数,可得速度和加速度响应。
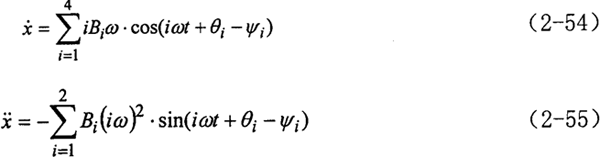
式中
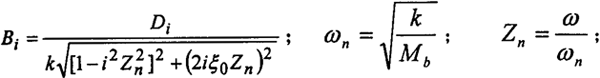
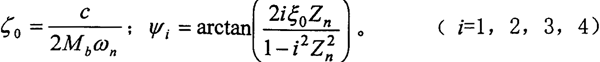
在y方向,由于受到一个方向和大小恒定的力作用,该力只对系统的静变形的位置有影响,而不会对系统在静平衡位置近旁振动的规律产生影响。同理,也可求的另一曲柄轴支点处的动态响应。
由于输出轴支点处不受激进力的作用,从理论上将该处无振动,实际上,由于各环板单位宽度上承受的载荷是不同的,且由于啮合处的啮合间隙和啮合刚度的变化,致使冲击不可避免。这也是试验中在输出轴承支撑处存在振动的原因。
2.5两种三环减速器的振动性能的对比
2.5.1 惯性力和惯性力矩对两种减速器振动性能的影响
完全平衡三环减速器传动机构满足了平面机构动平衡条件,其惯性力和惯性力矩均为零,这不同于基本型三环减速器的惯性力为零,而惯性力矩不为零。图2-12 所示为输入转速为1440r/min时基本型三环减速器支撑轴两端支撑轴承A和A′处的x和y方向单位宽度(cm)受力图。
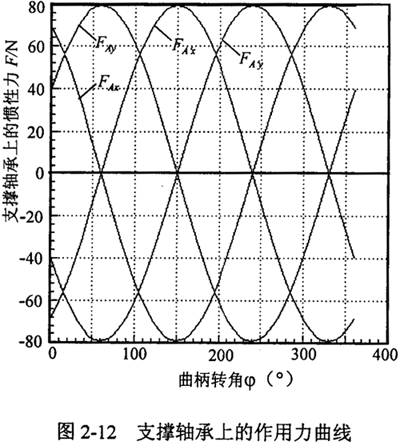
由于双轴输入完全平衡三环减速器的惯性力完全平衡,因而,各曲柄轴支撑轴承上作用的惯性力为零。基本型三环减速器的惯性力平衡,但惯性力矩不为零。
由本章第二节曲柄轴和输出轴的支撑轴承的受力分析和图2-12知,惯性力对完全平衡型的曲柄支撑轴承和两种三环减速器输出轴的支撑轴承无影响;而对于基本型三环减速器,惯性力在曲柄轴的支撑轴承处的x和y方向受到惯性力产生的激进频率为必冲击力的影响,由惯性力产生的曲柄轴两支撑处的动反力大小相等,方向相反。这说明,环板和偏心曲柄的惯性力(矩)的大小不影响曲柄轴和输出轴的支撑轴承,但影响曲柄轴的支撑轴承。
从理论上讲,惯性力和惯性力矩不引起完全平衡型三环减速器曲柄轴和输出轴支撑处的振动。
总的来说,基本型三环减速器的惯性力在曲柄轴两支撑处x和y方向均产生激进频率为ω的动反力,且两支撑处动反力的大小相等方向相反。这些动反力通过轴承作用在箱体上,是减速器产生振动的一个重要原因。完全平衡双轴输入式三环减速器的惯性力在曲柄轴和输出轴的支撑处均无动反力,从理论上讲,惯性力对箱体的振动无影响。但从减速器的受力分析知,曲柄轴各偏心曲柄处轴有不等的弹性变形,该变形使得曲柄和环板的惯性力不相等,对箱体产生冲击力,但这比对基本型三环减速器的影响小的多。
从惯性力的影响看,完全平衡双轴输入式三环减速器的性能较佳。
2.5.2 啮合力对两种三环减速器的影响
1.对基本型三环减速器振动性能影响 从支撑轴承的受力分析知,由于变啮合力的作用,输出轴两支撑处分别受到不等的周期性冲击力作用,即使双轴输入时,周期性的冲击力也存在,只是两侧的冲击力大小相等方向相反。曲柄轴也同样受到不等的周期性冲击力作目。这说明,啮合力对基本型三环减速器振动性能的影响较大。
2.对完全平衡双轴输入式三环减速器振动性能影响 从支撑轴承的受力分析知,在啮合力的作用下,输出轴各支撑处受力为零,即输出轴支撑不受啮合力的影响。而曲柄轴的y方向,啮合力的作用使轴两端支撑处产生相等的反作用力,由振动理论知,这个力只影响其静变形量;在曲柄轴的x方向,轴的两端支撑处受力相同,是一个周期性激进力。这说明,啮合力只对完全平衡双轴输入式三环减速器曲柄轴的x方向的振动有影响。
3.讨论 啮合力影响基本型三环减速器的曲柄轴和输出轴支撑处的振动只影响完全平衡双轴输入式三环减速器曲柄轴的x方向的振动,且影响较小。
从啮合力的影响看,完全平衡双轴输入式三环减速器的性能较为理想。
2.6 本章小结
本章在对基本型三环减速器进行分析的基础上,提出了环板拉压变形的积分求解公式,改进了三环减速器的变形协调条件,并给出了考虑惯性力和啮合力分别作用的变形协调方程;建立了考虑环板和转臂偏心轴(轴承)惯性力和重力的三环减速器的受力分析模型,并推导出了各环板所受的啮合力、环板转臂偏心轴承以及偏心轴和输出轴支撑轴承的受力表达式。对完全平衡双轴输入式三环减速器进行了受力分析和计算,计算结果表明:完全平衡双轴输入式三环减速器的力学性能良好。
依据连杆机构平衡理论,提出了完全平衡双轴输入式三环减速器的结构方案,建立了完全平衡双轴输入式三环减速器的理论基础。
依据振动理论,对完全平衡双轴输入式三环减速器进行了振动分析,建立了减速器的振动方程,得出了该减速器的输出轴和曲柄轴支撑的y方向不受激进力的作用,仅在x方向受到由啮合力引起的周期性的冲击力作用。求出了x方向振动的位移、速度和加速度响应。
研究了惯性力和啮合力对基本型三环减速器和完全平衡双轴输入式三环减速器振动性能的影响。得出了惯性力和啮合力对基本型三环减速器的曲柄轴支撑有冲击,啮合力对输出轴支撑有影响;惯性力对完全平衡双轴输入式三环减速器振动性能无影响,啮合力仅对完全平衡双轴输入式三环减速器的x方向振动性能有影响,且影响较基本型要小。
综上所述,完全平衡双轴输入式三环减速器有着较好的力学性能。
上一页
下一页