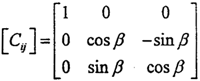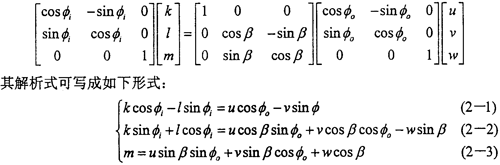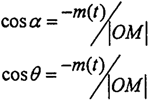分度机构剖析
环叉式万向联轴器实质上是由双联十字轴万向联轴器加导杆球笼式万向联轴器的分度机构所组成。环叉式万向联轴器同导杆球笼式万向联轴器的等角速传动特性的好坏关键就是由分度机构的性能所决定。对分度机构性能的深入分析，完全解析其特点十分有意义。
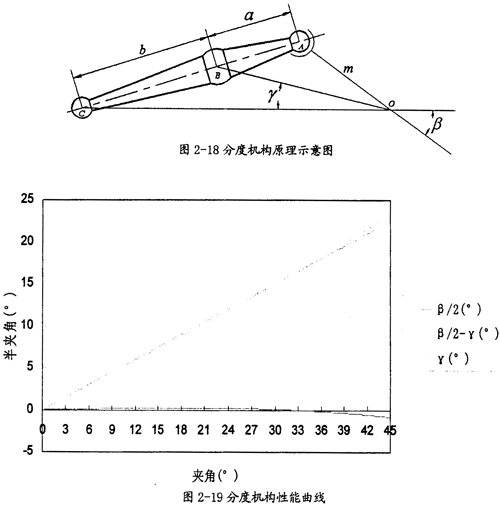
在环叉式万向联轴器中采用的分度机构布置形式见图2-17中红色部分。当叉轴1相对叉轴2有偏转时，分度机构的三个球头分别相对它们的配合构件转动，这样就会带动十字轴和十字环偏转一定的角度。根据现有的等角速传动理论，当十字轴和十字环偏转的角度为叉轴1相对叉轴2偏转角的一半时，将会把十字轴和十字环偏转到叉轴l相对叉轴2的等分角平面，这样传力点就会在等分角平面内，从而实现等角速传动。那么现在的关键问题是分度机构是否能正好将角度偏转一半。作出分度机构的原理简图如图2-18所示。机构中各参数的关系如下式：
m=18mm，a=9.7mm，b=27.7mm这里值的选取已经过优化）
现作出分度机构中理论半偏转角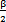
，实际半偏转角γ和它们的差的函数图形，如图2-19所示。
在图2-19中，可以看到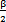，，γ的函数图形，在β角小于36度以前，几乎是重叠的，在36度以后，才开始有明显的差异，这一点从它们的差值曲线（图2-19中下面的紫红色曲线）也可以看出。这就是说，此机构在目前的尺度下在36度以前，它的分度性能是相当理想的，值得借鉴。不过从分度性能曲线上，可以看出，环叉式万向联轴器并非是完全的等角速万向联轴器，因为在36度以前的分度也有微小的差异。
2.3.1.2.2 THOMPSON 式万向联轴器
将环叉式万向联轴器的中间直线分度杆转变为球面分度机构，就成为一种新型的等角速万向联轴器，这就是THOMPSON式万向联轴器其结构如图2-20所示。
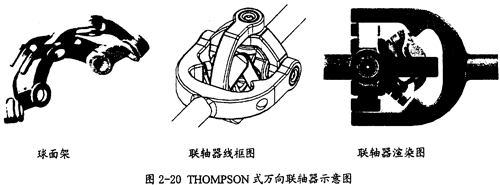
这种联轴器中通过用球面架（图2-20左边）来分度，相对环叉式万向联轴器来说，结构上是复杂了，但它将环叉式分度中的高副全变为了低副，在润滑上会非常优良，寿命就会大大提高。从上面的结构上看，这种改变在制造和装配上并未带来任何不便。据现有的实验资料表明，这种联轴器是一种等角速万向联轴器，目前这种联轴器在国内还未见有报导。
2.3.2 定心式等角速万向联轴器传动理论及其产品
2.3.2.1 定心式等角速万向联轴器传动理论
定心式等角速理论
a.两轴相交时，两轴交点与啮合点恒位于两轴线所成夹角的平分面上，可实现万向联轴器等角速转动（又称同步）；
b.两轴相错时，单一的万向联轴器联接不能实现等角速转动的目的。
理论证明如下：
万向联轴器的等角速条件
2.3.2.1.1 当输入、输出轴相交时的等角速条件
先将万向联轴器简化为如图2-21所示的数学模型。建立模型及坐标系如下：Zi和Zj分别代表输入与输出轴，Xi和Xj轴重合，均垂直于Zi和Zj所组成的平面。两轴间的夹角为β。特别须说明的是，本文所建立的坐标系均为右手坐标系，为了清晰起见，Y轴一般不再标出，可根据右手定则判断其方向。
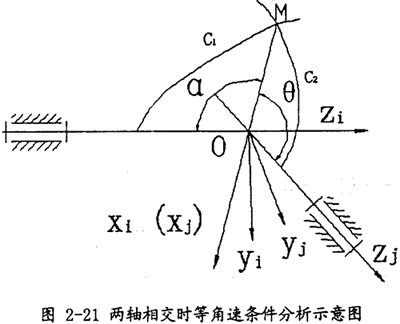
假设M点是两轴的啮合点（运动曲线C1和C2的交点，也就是传力点）假设初始条件为：当时间t=0时，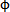
i（输入轴转角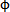），0（输出轴转角）均为零，在两坐标系OXiYiZi和OXjYjZj中，曲线Cl和C2的方程分别为：
如图2-21所示，坐标系OXjYjZj可以看作是坐标系OXiYiZi绕Xi（或Xj）旋转了一个角β度。旋转的方向余弦矩阵为：
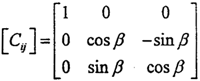
进行坐标变换有：（即由坐标系OXjYjZj变换到坐标系OXiYiZi其中（Xi，Yi，Zi），（Xj，Yj，Zj）分别表示某点在两坐标系中的坐标。）
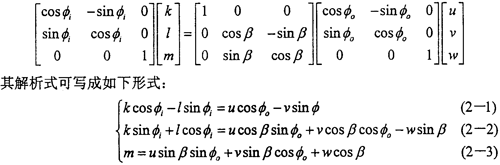
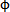假设i和β角已知，上述方程中只有三个未知量（0，t，s），因此用数值方法能够确定其解。
等角速条件的导出：
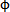假设该万向联轴器是同步的，可令i=0（i，0可取任意值）
则得：
msinβ=（1-cosβ）（ksini+lcosi）
由于γ可在一定范围内任意地取值，故有：
m=-w
综合以上所述，得到联接相交两轴的万向联轴器同步性的条件为：
由于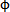i和β的取值是任意的，交点M也是任意的，因此两曲线方程满足上述同步条件时，才能保证输入、输出是完全同步。故它们的参数方程为：
设两曲线的交点M（啮合点）与两轴的交点O的连线OM与输入轴（Zi轴的负半轴）的夹角和OM与输出轴和夹角分别为：（在此处|OM|=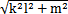
，表示啮合点与两轴交点间的距离。）
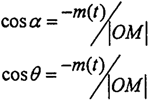
由此可得cosα=cosθ，由于0≤α≤180° 0≤θ≤180°。故有α =θ。简而言之，两相交轴完全同步的基本条件是：两轴交点与啮合点恒位于两轴线所成夹角的平分面上。
上一页
下一页
