4 数字齿面共轭求解与啮合界限曲线计算的数字化方法
4.1 引言
齿轮啮合是生产实践中常见的共轭运动,同时也是共轭曲面求解研究中的一个重要内容。本章基于上述共轭曲面的数字化方法和求解方法,利用啮合传动的规律,界定齿轮相对运动的啮合区,在啮合区内运用数字化求解原理和方法求解共轭曲面。这样做,一方面简化了计算,另一方面剔除了非啮合区零散的、不规则的“啮合点”的干扰,使计算结果更符合实际情况。本章对直齿面和鼓形齿面的数字化共轭曲面求解分别进行了研究,并对共轭求解中的关键问题啮合界限曲线的数字化求解进行了专门讨论。
4.2 直齿面的数字化共轭求解
以常用的直齿圆柱齿轮为例,直齿齿轮副在垂直于它们轴线的任一载面中的啮合情况是完全一样的,所以只需研究其中一个载面的情况,即平面上的啮合情况即可,因此,直齿齿轮啮合又称为平面啮合。
如果已知一个齿轮齿面的离散坐标数据、两齿轮的传动关系、两齿轮的相对位置,那么与已知齿面啮合的待求齿面也就可以求出。值得注意的是这里与回转曲面的共轭运动不同,齿轮啮合接触线的运动规律是复杂的,如果通过接触线来求解共轭曲面是不合适的,同时,如果考察一个已知齿面的啮合情况,会发现在齿轮回转一周过程中,这个齿面只是一次的进入啮合状态。这种情形可以用图4-1所示的相对运动形象地表示,图中两齿轮传动比为1:1,曲线段表示已知的齿轮齿面,它在所求齿轮坐标系内作公转加自转的相对运动。
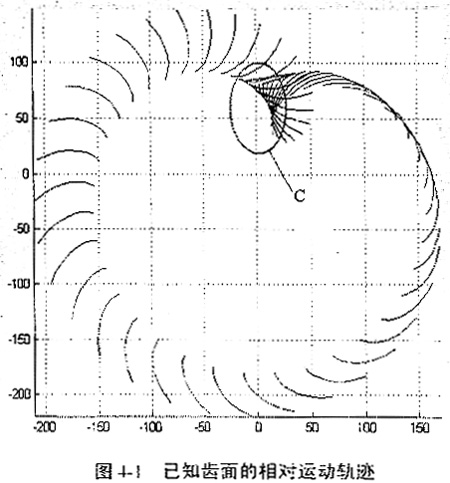
在已知齿轮齿面一个周期的相对运动所留下的运动轨迹中,我们可以看出,在区域C中出现了一个清晰的包络面,它就是所求的未知齿面,即两齿面在C区啮合,称C区为啮合区,而在C区之外,也会出现包络,但那只是几何意义上的共轭点,不产生真正意义上的啮合传动;已知齿面在啮合区域与非啮合区域有较清晰的界限;在啮合区域,已知曲面与所求齿面的共轭关系是简单的,无论是否会出现二次接触,这一区域的共轭曲面都可以用数字化共轭曲面求解方法求出。
在齿轮啮合的求解中,我们只求解啮合区内的共轭,这样做可以避开非啮合区内出现的共轭点对齿轮啮合求解的干扰,同时避免了不必要的计算。这样,确定啮合区域C即确定已知曲面进入啮合和结束啮合这一过程的运动参数tc就成为齿轮啮合求解的关键。
应用共轭曲面求解软件Conjugater1.0求得的齿轮齿面啮合过程和结果可以用图4-2、图4-3和图4-4表示。
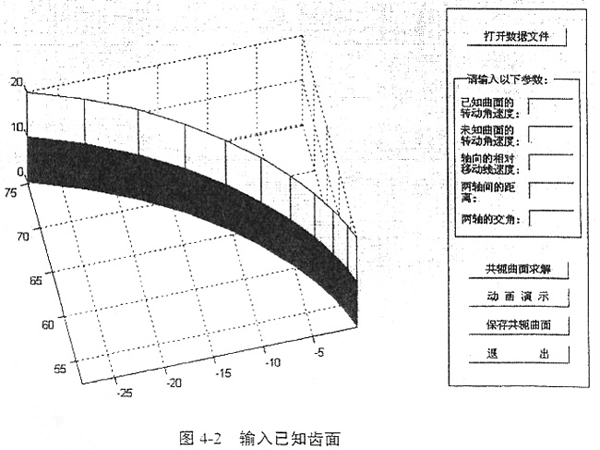
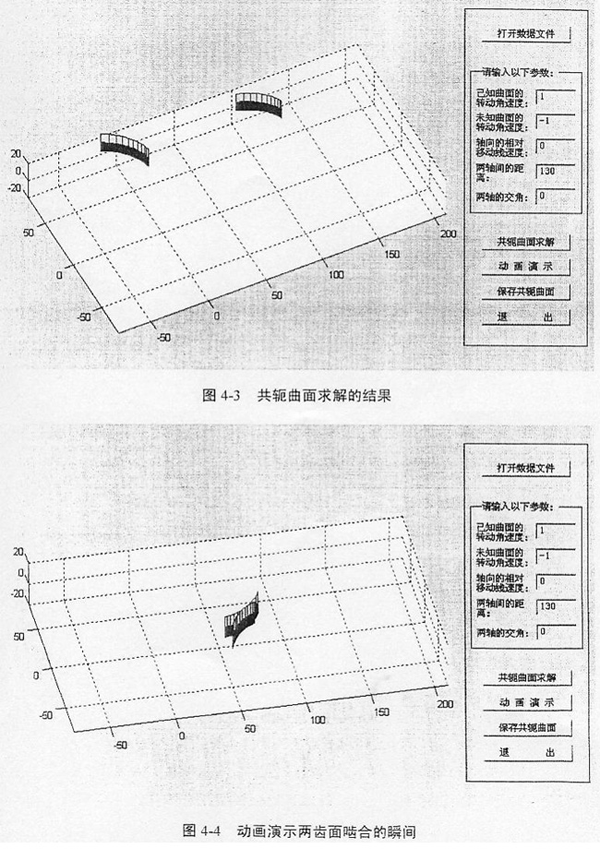
点击Conjugater1.0界面中的“动画演示”按钮,可以直观地看到两齿面转动和啮合的过程。
4.3 鼓形齿面的数字化共轭求解
由于齿轮在轴上的装配精度不能保证、轴承间隙不适当、齿轮轴弯曲变形等因素影响,导致两齿轮在端部非共轭接触,在端部齿根会产生过大的局部应力,严重时会造成齿轮的卡滞和轮齿的折断。采用轮齿的鼓形修形,可以避免在齿轮端部产生非共轭接触,避免齿轮折断,保证齿轮正常传动。鼓形修形也常用在齿轮联轴器的设计中,在传动轴有一定摆角的情况下,能够避免轮齿的干涉,实现正常的啮合传动。
所谓轮齿的鼓形修形,即在齿宽方向上齿厚从中央至两端连续减薄,经过这种修形后的轮齿称为鼓形齿。
鼓形齿是由直齿轮的啮合传动加两齿轮的相对摆动的双参数运动得到的,由包络定理可知,直齿轮的这种双参数运动可以转换为它的二次包络,第一次包络是直齿面绕齿面基准点的摆动形成包络面,第二次包络是此摆动包络面在啮合传动过程中各个位置形成的包络面。
一般书中是用经验公式得出鼓形齿的齿形,我们可以用数字曲面共轭求解的方法分别计算两次包络,从而求出鼓形齿的曲面。
4.3.1 直齿面的相对摆动包络面
设两齿轮的轴线分别为z1,z2,与之固连的坐标系分别为S1,S2,转动角速度分别为ω1,ω2,两轴线交角为θ。现暂不考虑两齿轮的啮合运动,只考察两齿轮的相对摆动,为使z2固定不动,可假设给系统添加一个绕z2轴且与ω2大小相同、方向相反的运动,如图4-5所示。则与齿轮固连的坐标系S1相对于S2的运动可以描述为绕z1轴的自转与绕z2轴的公转。

把以上的相对摆动具体化,考虑两坐标系的变换,在静坐标系S2中观察,整个S1坐标系只有2个自由度,即S1分别绕z1轴的自转和绕z2轴的公转。在交角不变的情况下两坐标系的关系可用图4-6表示。
这是固定摆动角度为θ时的情形,由此求出的齿面包络面满足摆动角度0≤θt≤θ的传动要求。
因图4-6所示的两坐标系的关系相对较复杂,为便于进行空间坐标变换的计算,可将变换S1→S2分解为S1→S3→S4→S2。如果规定从旋转轴的正向看下去逆时针旋转方向为正,顺时针方向为负,则S1→S3表示S1绕z1轴旋转-ω1t角度,S3→S4表示S3绕y3轴旋转-θ角度,S4→S2表示S4绕z4轴旋转ω2t角度。坐标系的分解变换如图4-7所示。

这种相对摆动的结果形成一个直齿面的包络面,在直齿面摆动的任何位置,两者都共轭线接触。利用两坐标系的几何关系和空间坐标变换,直齿面在静坐标系中形成的曲面族可用下式表示为
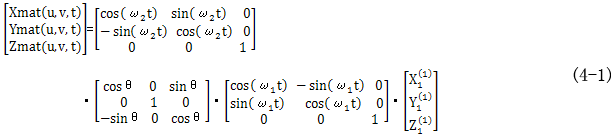
而在实际应用中,鼓形齿多用于联轴器传动,此时传动比为1,即ω1=ω2=ω,所以在鼓形齿联轴器传动中,上式可简化为
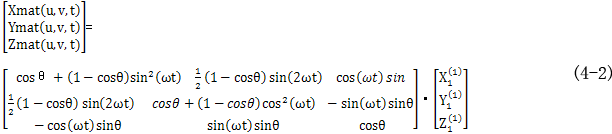
在已知曲面族的基础上,用前面介绍的数字化共轭曲面求解方法可以求出此曲面族的包络面,也就是已知直齿面Σ1在相对摆动时的包络面。
4.3.2 鼓形齿面
以上述计算出的摆动包络面为已知齿面,按照两齿轮的运动关系,用前述介绍的方法,求出摆动包络面的啮合面,这个啮合面既满足已知直齿面在一定角度范围内摆动,又满足两齿面啮合传动,它是一个鼓形齿面。在两齿面传动和已知直齿轮摆动的任何一个位置,鼓形齿面和已知直齿面都共轭接触。
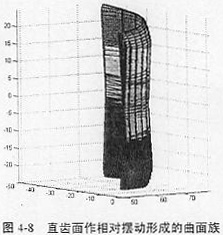
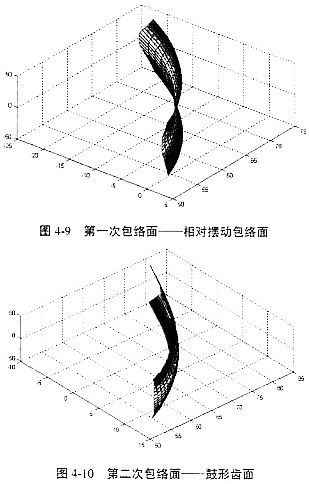
用Conjugater1.0求解鼓形齿面的过程和结果如下图4-8、图4-9、图4-10所示。这样,用数字化共轭曲面求解方法,通过计算直齿面的二次包络,就得到了严格满足共轭条件的鼓形齿面。
4.4 啮合界限曲线计算的数字化方法
4.4.1 接触线与两类界限曲线
已知曲面Σ1与共轭曲面Σ2在t时的接触线为Ct,那么Ct既是已知曲面Σ1上的曲线,又是共轭曲面Σ2上的曲线,我们把在与Σ1固连的坐标系S1中的Ct记为C1t,在与Σ2固连的坐标系S2中的Ct记为C2t。当t变动时,接触线Ct分别在Σ1、Σ2上形成一个单参数的空间曲线族{C1t}、{C2t}。
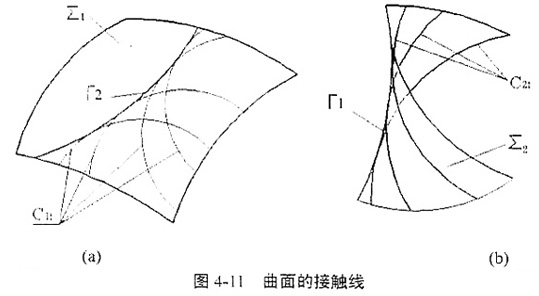
无论是已知曲面上的C1t还是共轭曲面上的C2t,当t取不同的值时,就得到不同位置的曲线,也就是说,{C1t}、{C2t}是以t为参数的曲线族,那么在曲面Σ1或Σ2上就可能存在曲线族{C1t}、{C2t}的包络线。在已知曲面Σ1上,如果曲面族{C1t}存在包络,那么以包络线为界可以把Σ1分成两部分(如图4-11a所示),一部分布满了接触线C1t,一部分则没有,这条包络线Γ2称为二界包络曲线,其上的各点称为二类界限点,也称为啮合界限点;对于共轭曲面Σ2,因为Σ2全部是由{C2t}组成的,所以如果曲线族{C2t}的包络存在,则此包络也就是曲面Σ2的脊线(如图4-11b所示),这条包络线Γ1称为一界包络曲线,其上的各点称为一类界限点,也称为根切界限点或曲率干涉界限点。啮合界限点可用于判断已知曲面上有效的啮合区域,根切界限点可用于避免共轭曲面的根切,这两类界限点对于共轭曲面的求解有着重要的意义,同时也是评价共轭运动质量的重要指标之一。
下面推导两类共轭包络曲线Γ1和Γ2的方程。
4.4.1.1 一界曲线方程
在共轭曲面Σ2上的接触线C2t的曲线族{C2t}可表示为 {C2t}: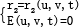 ,对包络条件来说,
,对包络条件来说,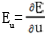 ,
,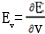 两偏导数不能同时为零。因为如果同时为零,说明包络条件中没有变数u、v,这时t只能等于常数,代入第一式,只能得到曲面族中的某一曲面,而不存在包络线。
两偏导数不能同时为零。因为如果同时为零,说明包络条件中没有变数u、v,这时t只能等于常数,代入第一式,只能得到曲面族中的某一曲面,而不存在包络线。
设Ev≠0,则可由E(u,v,t)=0中解出v=v(u,t),代入{C2t}的第一式得
{C2t}:r2*=r2(u,v(u,t),t)=r*(u,t)
如果{C2t}有包络Γ1,则Γ1可表示为
r2①=r2(u(t),v(u(t),t),t)=r2①(t)
{C2t}中任一条曲线C2t(t=常数)的切向量
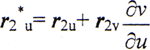
Γ1的切向量则可表示为
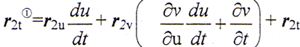
根据包络的定义可知,r*2u∥r2t①,所以
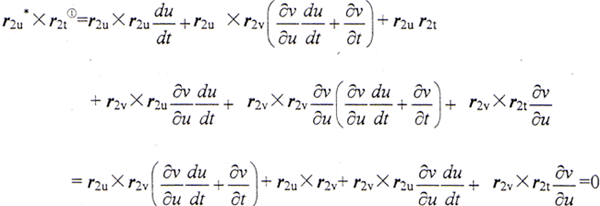
当以v=v(v,t)代入E(u,v,t)=0时,得恒等式E(u,v(u,t),t)=0,考虑Ev≠0,由上式即可导出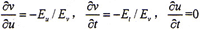 。于是,得到
。于是,得到
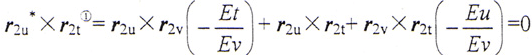
即 (r2u×r2v)Et+(r2v×r2t)Eu+r2t×r2uEv=0 (4-3)
为了使上述向量方程变为标量方程,使等式两端点积以r2u×r2v(≠0),并按拉格朗日恒等式展开,整理后得
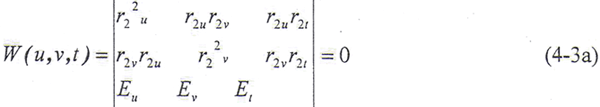
所以接触线的包络线Γ1的方程为
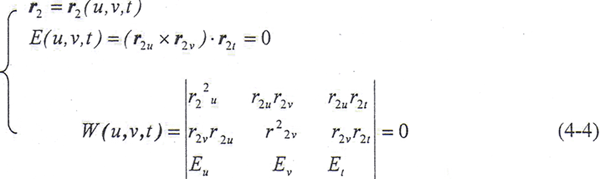
4.4.1.2 二界曲线方程
在已知母面Σ1上接触线族{C1t}可以表示为{C1t}: ,仿前,设Ev≠0,由E(u,v,t)=0解出v=v(u,t),代入上式的第一式,得
,仿前,设Ev≠0,由E(u,v,t)=0解出v=v(u,t),代入上式的第一式,得
{C1t}:r*1=r1(u,v(u,t))=r1*(u,t)
曲线族{C1t}的包络Γ2可以写为
r1②=r1(u(t),v(u(t),t)=r1②(t)
{C1t}中任一曲线C1t的切向量r1*u为
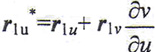
Γ2的切向量则为
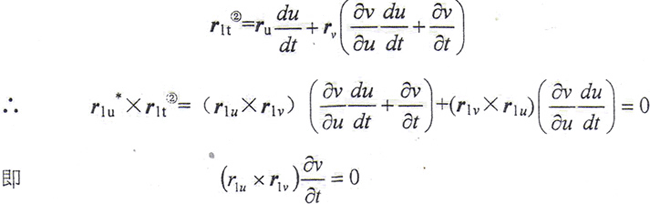
当Σ1为简单曲面时,有r1u×r1v≠0,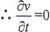 。将v=v(u,t)代入E(u,v,t)=0得
。将v=v(u,t)代入E(u,v,t)=0得
E(u,v(u,t),t)=0

4.4.2 啮合界限曲线的数字化求解
当已知曲面Σ1上存在二界曲线(啮合界限曲线)Γ2时,该曲线把已知曲面分成了两个区域,在曲线Γ2的一侧,布满了接触线C1,t1,C1,t2…,这部分区域称为工作区,在曲线Γ2的另一侧,没有接触线,这部分区域称为非工作区。共轭曲面上的接触线分别为C2,t1,C2,t2…。今在Σ1的工作区内取一点P1(1),它既是C1,t1上的点又是C1,t2上的点。可以看出,在t=t1时,由于接触线C1,t1与C2,t1重合,即C1,t1=C2,t1,所以P1(1)与C2,t1上的点P1(2)共轭接触,但在t=t2时,P1(1)点又作为C1,t2上的点而与C2,t2上的P1(2)′点共轭接触。再在已知曲面工作区内取P2(1)点,也有类似的情况,即在不同的时刻t=t1,t=t2,点P2(1)分别与共轭曲面Σ2上的不同点P2(2)先后共轭接触。对于在Γ2上的点,因为它只属于工作区内的一条接触线,如M1(1),它是接触线C1,t1与界限曲线Γ2的切点,因此它只属于C1,t1,并且只在t=t1时与共轭曲面内点M1(2)共轭接触。这样,在已知曲面的工作区内的任何一个点,都在共轭曲面Σ2中有先后两个共轭接触点,这种现象就叫做二次接触。只有在已知曲面Σ1的界限曲线Γ2上的点,才不存在二次接触。
由上面分析可以看出,用解析方法求啮合界限曲线是很复杂的。为减少人工计算的负担和充分利用数字化共轭曲面求解理论和方法,在前面介绍数字化共轭曲面求解的基础上,本文提出一种啮合界限曲线的数字求解方法。在数字化共轭曲面求解模型和求解步骤中,共轭曲面是通过考察已知曲面的每一节点的运动特性,通过计算并记录每一个节点在整个运动过程中出现共轭的位置来求解的;但在运动过程中,会出现某些节点,在整个运动过程中都不会出现共轭点,即这些点在整个运动过程中,并没有参与共轭,这些点的集合就是上面提到的啮合界限曲线一侧没有参与两曲面接触和共轭的部分。
在前述的计算中,用插值方法得到一个以t为自变量的连续函数E(t),然后求出使E(t)=0时t的值tk,这种方法得到的tk值,不同于一般通过优化算法使E(ui,vj,t)在一系列有限值中取最小值时的t值,而是利用插值得到的E(ui,vj,t)=0时t的精确值;如果tk存在,则一定有E(ui,vj,t)=0,该节点参与了共轭,反之,则该节点没有参与共轭。由此,我们可以通过判断tk的存在与否来确定哪些节点在运动过程中没有参与共轭,并在计算步骤中加上一个判断语句,且记录下不参与共轭的节点在已知曲面上的u,v值,这样,在共轭曲面求解的同时,也计算出了已知曲面上参与和不参与共轭的节点,这两类节点分别形成已知曲面的两个区域,即工作区和非工作区,它们的分界线就是啮合界限曲线。
4.5 小结
本章在理论创新的基础上,对工程中有代表性的直齿轮和鼓形齿联轴器传动进行了研究,并对直齿面和鼓形齿面作了数字化共轭求解,得到了与之相应的共轭直齿面和鼓形齿面。在共轭求解中充分考虑和利用各自的共轭运动特性,特别在鼓形齿联轴器的运动特性分析和数字化求解方面,是对以往求解方法的一次突破,具有创新意义。本章还推导了共轭求解中的两类共轭包络曲线方程,提出了求解啮合界限曲线的数字化求解策略与计算方法,开创了用数字分析方法研究啮合传动特性的新途径。
上一页
下一页






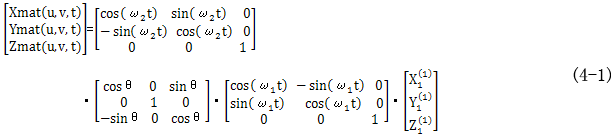
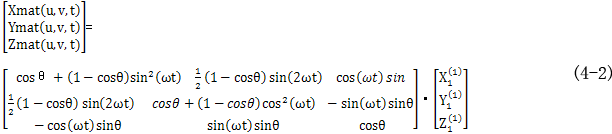



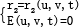 ,对包络条件来说,
,对包络条件来说,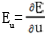 ,
,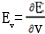 两偏导数不能同时为零。因为如果同时为零,说明包络条件中没有变数u、v,这时t只能等于常数,代入第一式,只能得到曲面族中的某一曲面,而不存在包络线。
两偏导数不能同时为零。因为如果同时为零,说明包络条件中没有变数u、v,这时t只能等于常数,代入第一式,只能得到曲面族中的某一曲面,而不存在包络线。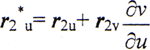
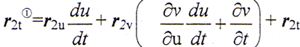
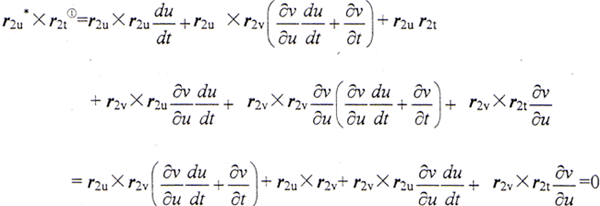
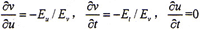 。于是,得到
。于是,得到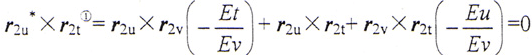
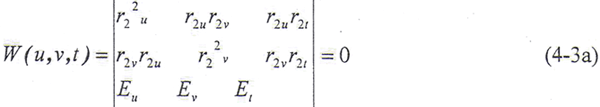
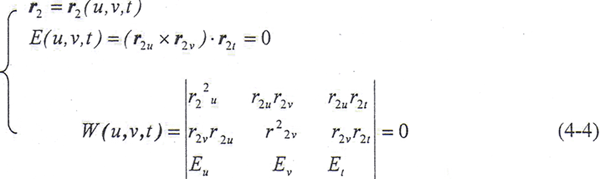
 ,仿前,设Ev≠0,由E(u,v,t)=0解出v=v(u,t),代入上式的第一式,得
,仿前,设Ev≠0,由E(u,v,t)=0解出v=v(u,t),代入上式的第一式,得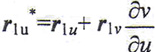
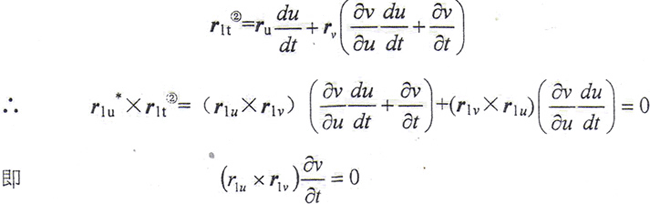
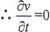 。将v=v(u,t)代入E(u,v,t)=0得
。将v=v(u,t)代入E(u,v,t)=0得