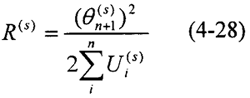|
4.4系统固有特性及势能分布率
要分析和评价减速器的扭振特性,必须先计算出系统的各阶固有频率、相应的主振型和各阶模态柔度。
4.4.1固有频率和主振型的确定
欲求系统的各阶固有频率和主振型,需求解系统的无阻尼自由振动方程。当系统自由振动时,激励力矩和阻尼均为零,此时系统的数学模型以复数表示为:

根据边界条件,系统自由端状态矢量中M=0,固定端Θ=0。代入式(4-23)得

式(4-24)有非零解的充要条件是
G11=0 (4-25)
当不计阻尼时,惯性元件的传递矩阵是系统振动频率的平方ω2的函数,弹性元件的传递矩阵仅与元件的刚度有关,所以系统累积传递矩阵的元素G22是ω2的函数,并且ω2的阶次与系统的惯性元件数目相同,所以满足式(4-25)的振动频率均为系统的固有频率。
求出系统的各阶固有频率ω后,即可求出相应各阶主振型和系统主振型。倘若取第s阶固有频率ωs代入下式,便右逐一求出各元件的第s阶状态矢量Θ1(s)、Θ2(s)、…、Θn+1(s)。

所取得的一系列Θ(s)值,便是第s阶主振型{Θ(s)},它表示系统以ωs频率扭振时,各惯性元件扭转角大小的相对比值。将各阶主振型向量合并即可得到系统的主振型。

4.4.2 模态柔度和势能分布率的确定
在建立了反映传动系统动态特性的数学模型的基础上,可对结构进行动力修改或优化设计以使所设计的系统具有良好的动态特性。通常的结构动力修改问题,是要求把结构的振动强度或动柔度限制在一定的范围内。有效的修改过程是先找出结构的薄弱环节,然后有针对性的修改薄弱环节的局部结构,从而使整个系统的动态特性满足要求。确定结构薄弱环节并以此为依据进行结构修改的方法主要是考察系统的模态柔度和势能分布率。
由于系统的最大能量Emax是与振型向量{Θ}的平方成正比的,不论阻尼大小如何,这个比例关系总是一定的。因此,模态柔度是一个与阻尼无关的参数,其大小仅取决于系统的结构参数和物理参数。改变结构参数、物理参数的大小和配置方式,均将使其发生明显的变化。系统的第s阶模态柔度R(s)的定义为
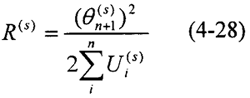
式中θn+1(s)——系统末端在第s阶模态振动时的扭振幅值(rad);
Ui(s)——系统中第i 个弹性元件在第s阶模态振动时的势能。其值为

式中Ui(s)——系统中第i 个弹性元件在第s阶模态振动时的转角。
模态柔度的大小表明了该阶模态的危险程度。模态柔度越大,说明该阶模态越危险。但要找出造成该阶模态危险的原因,确定结构修改的部位和修改内容,仅凭模态柔度值还不够,还必须考察各个弹性元件的势能或势能分布率。势能分布率定义为

势能分布率的大小表明系统中弹性元件变形能的大小,势能分布率最大的元件也就是系统的最薄弱环节,即造成该阶模态危险的主要原因。据此可以确定相应的改进措施,以提高系统的动态性能。
4.5 动力学模型参数的确定
在滚柱活齿减速器扭振动力学模型中,其参数包括几何参数、物理参数和外载荷参数三类。几何参数在减速器系统设计完成后即己完全确定,在物理参数中有质量参数(如转动惯量)、刚度参数(如活齿副啮合刚度、传动轴扭转刚度等)和阻尼参数(如轴类零件扭转阻尼)。其中,转动惯量在系统设计后即可计算求得,传动轴扭转刚度可以按材料力学方法计算。下面给出活齿副啮合刚度和轴类零件扭转阻尼的计算方法。
4.5.1 活齿副的啮合刚度
活齿副的啮合刚度是指工作时活齿副共同抵抗变形的能力,它与啮合副的综合弹性变形有关。啮合副的综合弹性变形是指活齿副在啮合过程中弹性变形的总和,表示为
δ=δ1+δ2 (4-31)
式中
δ1——活齿的弹性变形(mm);
δ2——波发生器、活齿架或中心轮的弹性变形(mm)。
活齿副啮合刚度k可表示为:

式中
k1——活齿的接触刚度(N/mm),k1=1/δ1;
k2——波发生器、活齿架或中心轮的接触刚度(N/mm),k2=1/δ2。
只要求出活齿及与活齿啮合件的接触变形,即可确定啮合综合刚度。接触变形的计算按下式进行:

式中
E——材料弹性模量(N/mm2);
B——齿宽(mm);
4.5.2 轴类零件扭转阻尼
轴类零件的扭转阻尼主要是材料阻尼,根据H.H.Lin.和C.Lee.等的分析,其扭转阻尼可利用下式进行计算:

式中ks——轴类零件的扭转刚度(N·mm/rad);
ξs——轴类零件的扭转阻尼系数,根据D.R.Houser等的试验研究,ξs一般取0.005~0.075;
I1,I2——分别为轴类零件两端惯性元件的转动惯量(kg·mm2)。
4.6 滚柱活齿减速器扭振动态特性分析
利用前面建立的滚柱活齿减速器系统的动力学模型对减速器系统进行扭振分析,找出系统的固有特性,即固有频率和主振型。由于轴承的旋转阻尼很小,这里忽略不计。根据减速器各元件实际尺寸计算得到各惯性元件的等效转动惯量、弹性元件的等效扭转刚度如表4-1所示。
表4-1惯性元件的等效转动惯量和弹性元件的等效扭转刚度
| I1(kg·mm2) |
I2(kg·mm2) |
I3(kg·mm2) |
k1(N·mm/rad) |
k2(N·mm/rad) |
k3(N·mm/rad) |
| 2.2342×103 |
2.0833×104 |
7.2384×105 |
1.3313×1011 |
1.3313×1011 |
2.6864×1011 |
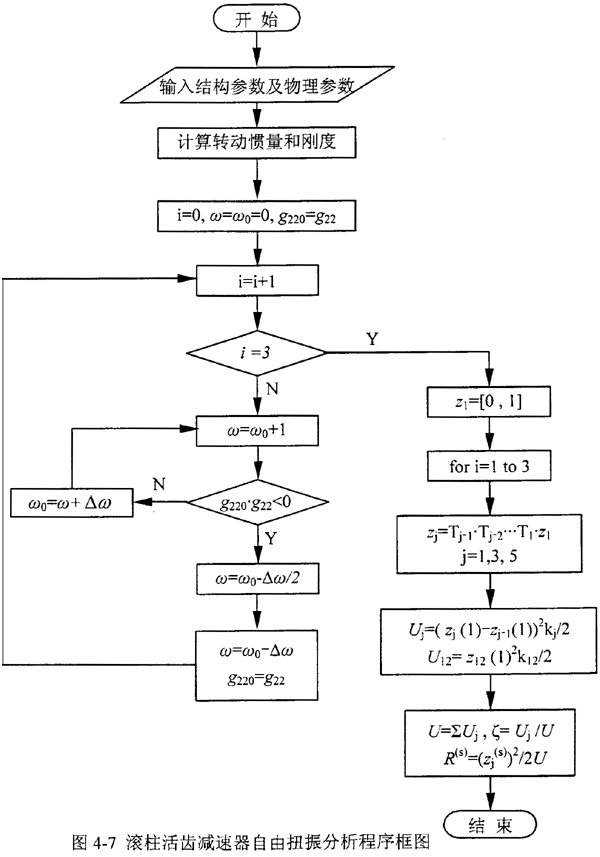
根据前面介绍的方法,在计算机上编程对减速器的扭振动力学特性进行分析,其程序框图见图4-7所示。在计算机上运算时,按照确定的频率步长对频率方程扫频,作出“G11-ω”曲线,如图4-8所示,凡G22=0时的ω值,就是系统的固有频率。有关固有频率、势能分布率和模态柔度的计算结果见表4-2。另外,利用该程序还绘制出图4-9所示的减速器系统的振型曲线。
表4-2 滚柱活齿减速器扭振动力学分析结果
| 固有频率(×103rad/s) |
0.1896 |
2.4281 |
8.1645 |
| 主振型 |
{1.0000,0.9994,0.992} |
{1.0000,0.9011,-0.1358} |
{1.0000,-0.1186,9.4318} |
势能分
布率 |
弹性元件1 |
0.4551 |
0.5508 |
0.0527 |
| 弹性元件2 |
0.4545 |
0.4472 |
0.00074227 |
| 弹性元件3 |
0.0904 |
0.0020 |
0.9465 |
| 系统模态柔度×10-7/rad(N·mm)-1 |
3.3637×10-5 |
7.6298×10-7 |
3.5234×10-4 |
通过表4-2中的分析结果我们可以看出,三阶(8.1645×103rad/s)系统模态柔度最大,所以该阶模态是危险模态。要找出造成该阶危险模态的具体原因,我们可以考察各弹性元件的势能分布率。从表4-2中可以看到,此时3号弹性元件的势能分布率最大,这说明在扭转时,它的弹性变形能最大,即它是最薄弱环节,是造成危险模态的主要原因。从这个结论出发,便可以采取相应措施来改进设计方案。通过适当增加活齿架的壁厚或减小输出轴长度来提高扭转刚度,便可改善该减速器的动态特性。动态性能好的系统应该是各阶模态柔度小而且每阶模态中各元件的能量分布均匀。为了达到这个目标,可以按照上述方法继续调整有关弹性元件的扭转刚度,直到获得满意的结果为止。
在负载变化和误差较小的情况下,滚柱活齿减速器系统的激励频率就是啮合刚度的变化频率。它的计算如下:
ω=2πni/60i=34.7rad/s
式中ni——输入轴转速(rpm);
i——传动比。
由表4-2中结果可知,减速器系统的一阶基频为189,6radis,系统基频远大于激励频率,因此该减速器的振动水平较低,振动和噪声较小。
4.7 本章小结
1.通过将组成滚柱活齿减速器的各个零件简化成相应的惯性元件和弹性元件,建立了减速器的系统动力学模型;通过将各惯性元件和弹性元件转换到输入轴上,得到了适于用传递矩阵法进行动力学分析的链状动力学模型。

2.在建立起惯性元件和弹性元件动力学数学模型的基础上,利用传递矩阵法建立了减速器系统的动力学数学模型;给出了活齿副啮合刚度和轴类零件扭转阻尼的计算公式。
3.利用所建立的动力学模型,通过编程分析了井下驱动螺杆泵采油减速器样机的自由振动。得到了该系统的固有频率、模态柔度和各阶振型等动态特性参数。结果表明,该减速器具有良好的动态特性。
4.根据所求的模态柔度和各弹性元件的势能分布率,找到了危险模态及导致危险模态的薄弱环节,为进一步改进其结构,提高动态特性,提供了理论依据。
上一页
下一页
|