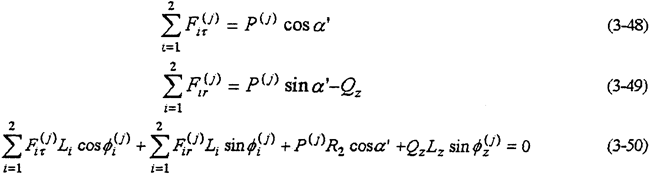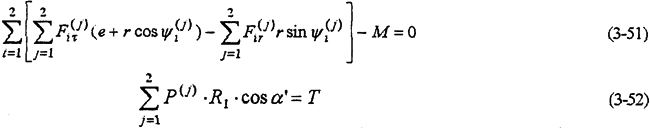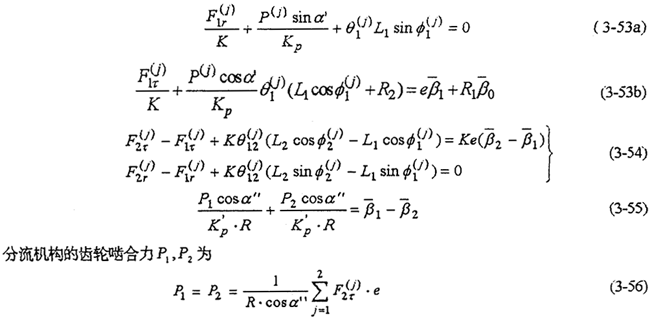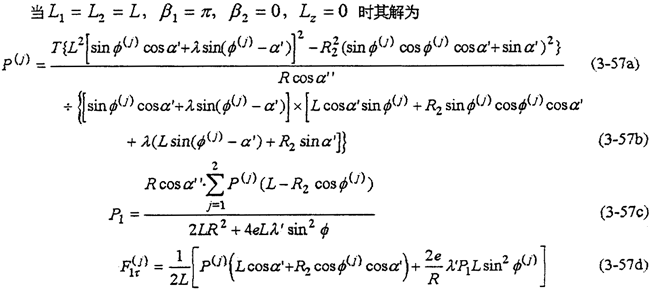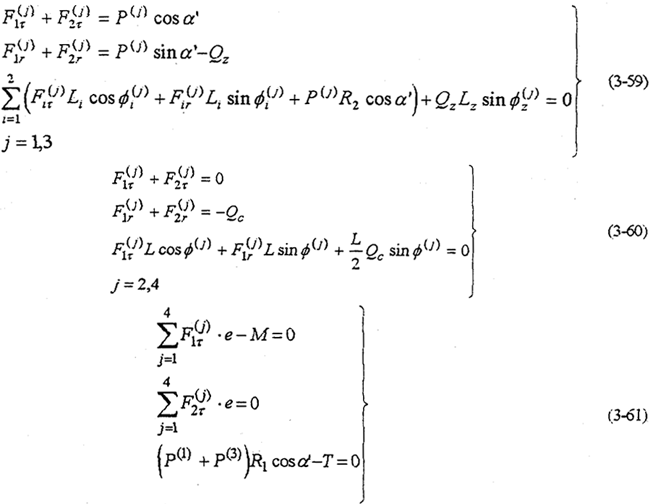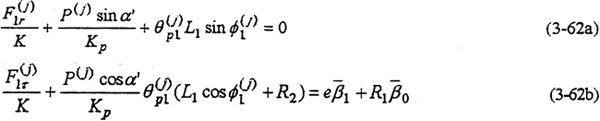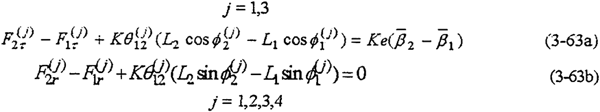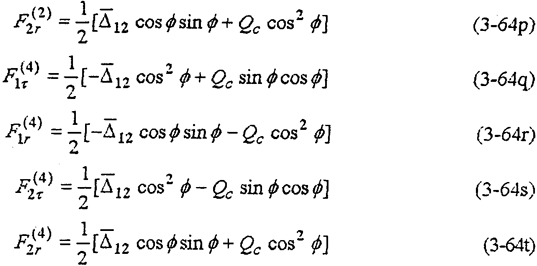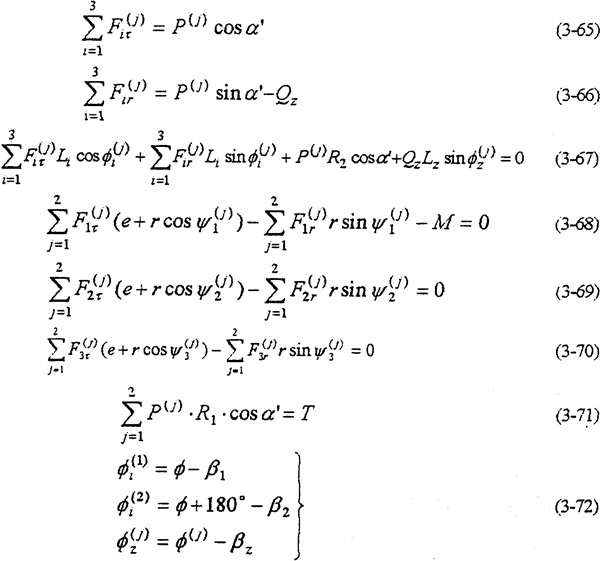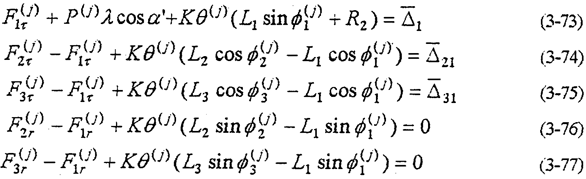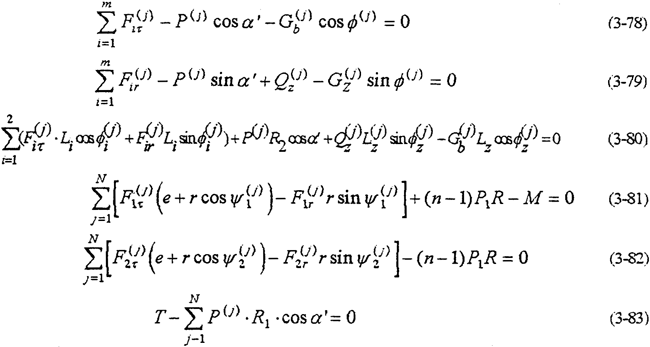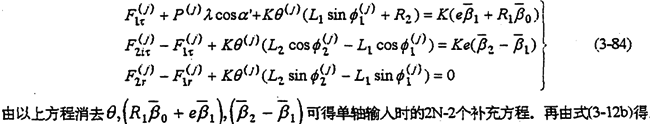3.5二齿环内齿行星传动的动力分析模型
二齿环内齿行星传动机构与一齿环内齿行星传动机构的结构形式基本相同。它是由两片相位差为180°的行星齿板与输出齿轮啮合传递运动和动力的。
3.5.1双轴式双轴输入二齿环内齿行星传动
该类传动是通过定轴传动机构使动和传递到两根高速轴上形成双轴输入，见图3-4所示。由动力分析基本方程令m=2，N=2得
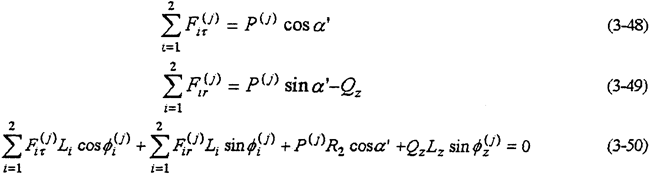
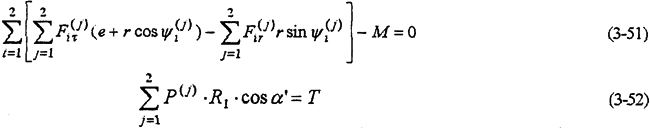
由式（2-7）计算得该结构形式的静不定次数S=3。根据约束高速轴之间的位移协调方程式及约束高速轴与低速轴之间的位移协调方程式（3-11）和（3-12b）及（3-13）得
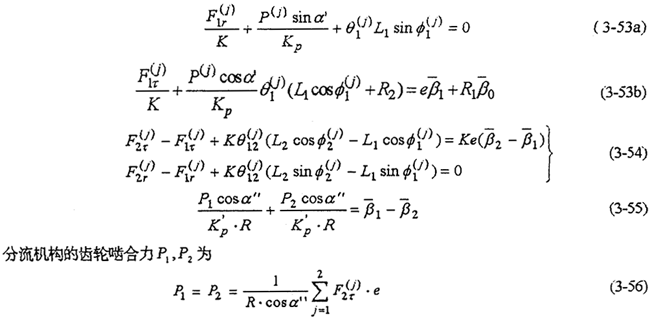
由式（3-53）消去
可得到一个补充方程，由式（3-54）、（3-55）消去
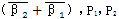可得两个补充方程，一共恰好3个补充方程。故由式（3-48）～（3-56）构成了双轴输入式二齿环内齿行星传动机构的动力分析模型。通过计算机可以求出任意布置（高速轴）的结构形式的解。下面经出对称布置和偏置式的解。
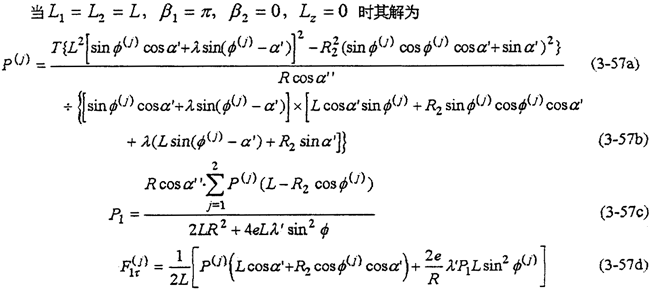
由式（3-57）及（3-58）比较可知，偏置式受载比对称式的受载波动大（随转角），因而使箱体产生的振动也就更强烈。
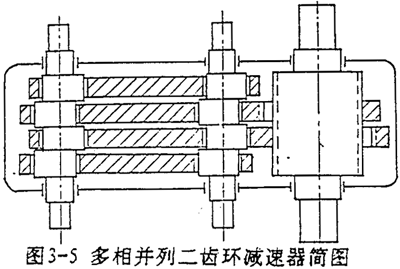
3.5.2多相并列双曲柄输入式二齿环内齿行星传动
这种传动的结构形式如图3-5所示。它由四相（套）双曲柄机构作为传动的输入机构。相邻两相机构之间的相位差90°。其中有两相双曲柄机构的连杆带行星内齿轮，即为传动机构的两片行星齿板。齿板之间的相位差互为180°。该机构的动力分析基本方程为
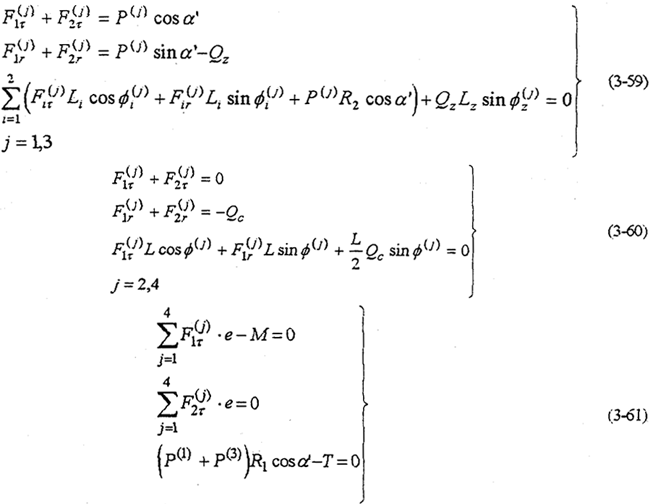
该传动机构的静不定次数S=4。由高速轴之间的约束条件式（3-11）及高速轴与低速轴之间的约束条件式（3-13）得
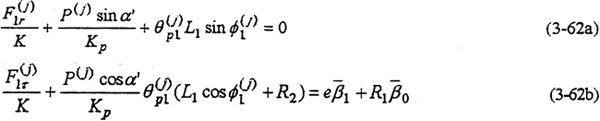
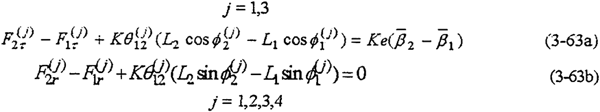
以上两式消去
——共可得到4个方程。由式（3-59）-（3-63）就构成多相并列双曲柄机构输入式二齿环内齿行星传动机构的动力分析数学模型。
当L1=L2=L，β1=π，β2=0时，解动力分析模型得：
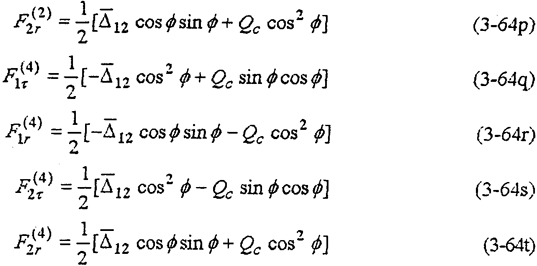
由解式（3-64）可见，啮合力并不等于常量，而是与转角φ及连杆惯性力QC等因素有关。设计时应保证P（j）≥0，以免内齿轮副发生干涉，出现负向啮合图现象。
3.5.3 多轴式二齿环内齿行星传动
采用多轴（多曲柄机构）式的内齿行星传动是为了克服机构出现不确定的“死点”位置。故这种机构可以实现单齿环传动。但是为了增加传动装置的承载能力，往往也采用二齿环或多齿环传动形式。由于传动齿板增加，各从动转臂高速轴不再属于二力构件。因此各轴的切向行星轴承载荷F(j)it≠0。以三轴式为例其动力分析基本方程为
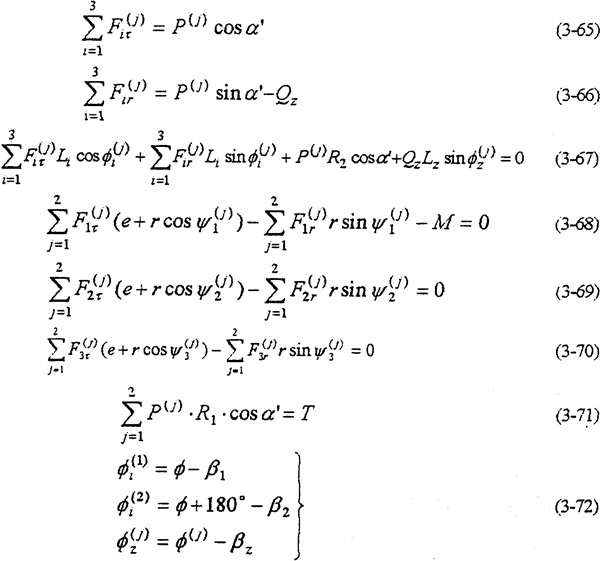
通过静不定次数计算，S=5。根据各轴之间的约束条件得
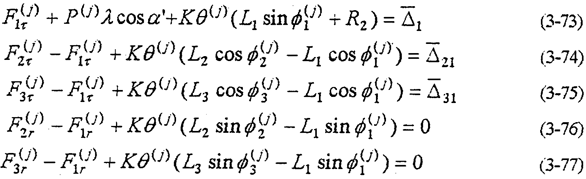
由以上10个补充方程消去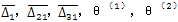
便可剩下5个方程。由方程式（3-65）～（3-77）构成了三轴式二齿环内齿行星传动机构的动力分析数学模型。
3.6 多齿环内齿行星传动的动力分析模型
多齿环内齿行星传动就是平行轴多相并列双曲柄输入式少齿差人齿行星传动。齿板通常在三片以上，采用双轴（两根高速轴）布置。如三环减速器、四环减速器等传动装置。在实际结构中，根据需要可双轴输入，也可单轴输入。由于各相之间是通过转臂高速轴传递扭矩来克服机构“死点”，以及各行星齿板变形不一致，各种加工、安装误差等原因，不能孤立地把各曲柄（偏心套）当作二力杆件处理。即各F(j)it≠0。故其动力分析基本方程为
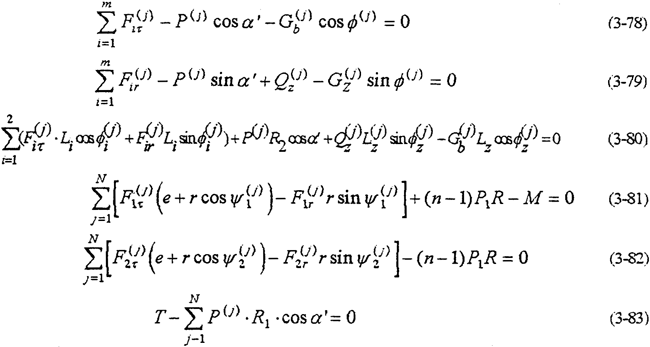
式中当n=1时，为单轴输入，n=2时，为双轴输入。
该类传动机构的静不定次数为S=2N+n-3。单轴输放时S=2N-1。根据各轴之间位移约束条件式（3-14）得。
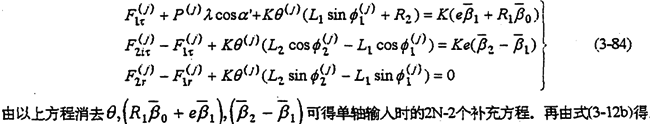
由式（3-78）～（3-85）就能完全确定整个机构的动载荷。当N=2时为二齿环传动，N=3时为三齿环传动，N=4时为四齿环传动。因此式（3-78）～（3-85）实际上是多轴式以外的各各类型的内齿行星传动机构的动力分析方程。
3.7 考虑运动副间隙的动力分析补充方程
在前面的动力分析模型中，均忽加重了机构的间隙误差。实际上间隙误差是引起内齿行星传动机构产生冲击振动的主要原因之一。在没有间隙误差时，内齿行星传动的输入机构是平行四边形双曲柄机构，机械可以顺利运转。但一旦有间隙误差时，就不再是平行四边形机构，而变成了曲柄摇杆机构。如要使整个机构连续整转，必须要克服曲柄摇杆机柄的死点，而产生载荷冲击，引起传动机构振动。由于间隙误差引起的载荷冲击通常比正常时的载荷要大几倍甚至10倍以上。因此，如要准确地对内齿行星传动进行动力分析，必须要把机构的间隙误差考虑进去，建立完整的动力分析模型。
当只考虑接触变形和运动副间隙时，各轴之间的约束方程为：
式（3-86）、（3-87）就是考虑间隙误差的动力分析补充方程。
上一页
下一页
