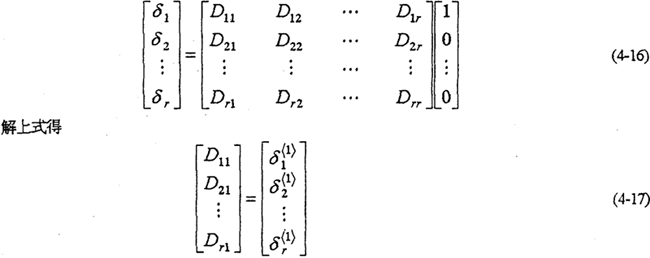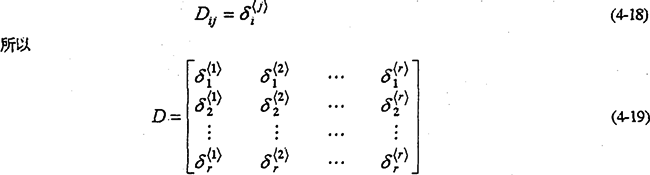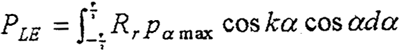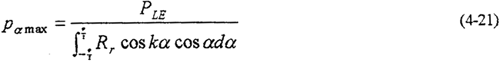�ڳ����dz��ִ�������ı���λ���о�
4.1����
��һ�¶��ڳ����dz��մ��������Ķ�����ģ������ϵͳ���о������о��з��֣�����λ��Э�����䷽��ʱ�������뽫����λ���빹������Ȼ�ն���ϵ���任������Ҫ�����������صĹ�ϵ���Խṹ����������Լ����ֵȣ������������е��йؼ��㹫ʽֱ�ӽ�������λ�������գ��Ĺ�ϵ��Ȼ���������dzݰ塢ƫ���������������ṹ��״����ֻ�ܽ����ΰ��Ӵ����ν��д��������ýӴ�����Ӵ��ն�ϵ��֮�ȴ���λ�ơ����ַ�����㣬����ֱ�ӵ�����Ľ�����ʺ����غɲ����������С�Ĵ��������������ظ��ٴ�����˵�������������������Ƚϴ��ر������dzݰ�ij�Ȧ�������λ�ýǶȱ仯�ģ������Ҳ�������ϳݱ仯���仯��
��ˣ��ݰ�ĸն��ڹ��������б仯Ҳ�ܴ�����Ϊ���������dzݰ���ij���λ���������ڳݰ��������غɣ��Ĺ�ϵ������Ӵ�����������ij���λ��ֻ��õ����ؼ��õ���ȣ��նȣ��йء�����ͨ���ݰ���������ϵ��������ϵ�����ڳݰ���������������ӳij���λ�ơ�������λ�������Ĺ�ϵ������ȷ��̡����dzݰ���ȷ����е����ϵ�����湤��λ�æ�(j)�仯�����ǹ̶�ֵ�����ϵ�������ڲ�ͬ�Ĺ���ʱͨ������Ԫ������ֵ���㷽����ȷ��������������Ԫ���������dzݰ弰ƫ�����ڲ�ͬ����ʱ�����ϵ����������λ�������Ĺ�ϵ�����ᡢ��С�����ֵ������λ�������Ĺ�ϵ�������е����۹�ʽ��ʾ��
4.2���������ȷ��̼�����ȼ���
��ȷ������ǵ������λ�Ʊ���ʽ������Ԫ���еĸնȷ��̾��ǵ�����ڵ�λ����ڵ���֮��Ĺ�ϵ

��ʽ��4-1��������ǵ�����ڵ�λ�Ƶ�����ʽ�����뽫��ת��ֻ�뵯�������غ��йصĽڵ�λ���Ժ�ʽ�����������ڳ����dz��ִ����Ķ��������С�����ʽ��4-1���е��ܸնȾ���K��һ���������������������Բ���ֱ�ӽ����λ�Ʊ���ʽ�������뿼��ʵ�ʱ߽��������Լ�Ϊ������ָ����˶����Ծ���ĵ��������ij��ڵ���λ�Ƶ�Լ�������������ܸնȾ���KҪ����Ӧ�ı����ʹ�ܸնȾ����Ϊ������������߽�λ��Լ���ķ������ο����ס�
����Լ��������ʽ��4-1������

ʽ��4-6�����ǵ�������ɢ������Լ�������Ľڵ�λ�Ʊ���ʽ�������������ȷ��̡���Լ����������n��ڵ�λ�ƣ���

ʽ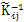 ��i=1��2������n��j=1��2������n���ǵ���������Ӿ���
��i=1��2������n��j=1��2������n���ǵ���������Ӿ���
������ȷ���Ϊ
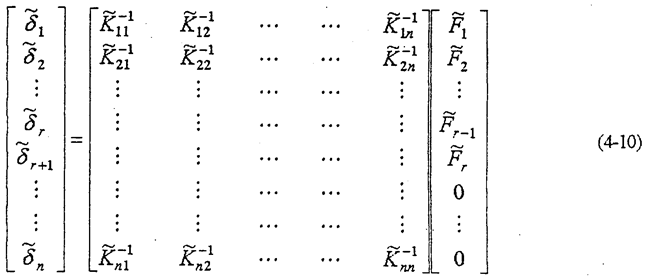


ʽ��4-12�������������õ�λ�Ƽ����������Ĺ�ϵʽ��
��Ⱦ����繹���IJ��ϡ�������״�Լ�����������״�������йء����и�Ԫ�ؿ������μӵ�λ�غɣ���ʽ��4-12������ȷ��������ʽ��4-14����F1=1��F2=F3=��=Fr=0����ʽ��4-12����
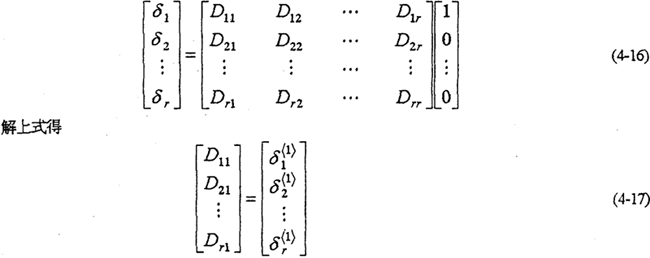
��ʽ��Di1=��<1>i����F1���õ�ӵ�λ�غɼ���������ϵ��ֵ��ͬ���ɷֱ���F2��F3������Fr���õ�ӵ�λ�غɣ������������
ϵ��ֵ�����ǵõ�
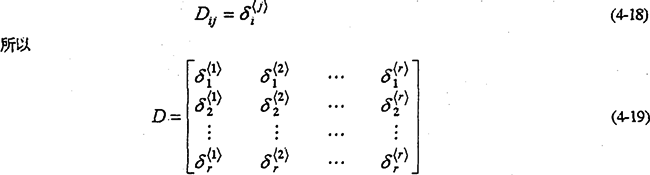
ʽ��4-19������������Ԫ��ͨ���ӵ�λ�غ���õĵ�������Ⱦ���
4.3ƫ�������dzݰ����ȼ���
���Ͻڽ���֪������������ϵ���������ͨ������Ԫ�����ӵ�λ�غ�������ȷ������ˣ�ƫ�����ڳ����Ǵ����ݰ����ȼ��㣬ʵ�����Ƕ����������Ԫ��ģ������������SHQ40����������Ϊ������SUN����վ��ʹ��I-DEAS�����е�����Ԫģ�����ƫ�����ݰ�����ϵ����
4.3.1ƫ��������Ԫ��ȼ���
ƫ����ʵ��ģ����ͼ4-1��ʾ�����������������У�ƫ�����������ɵ�������������λ�ƣ�����w=0����z=0����zy=��zx=0����ˣ����Խ�ƫ����Ϊƽ��Ӧ��������������

ͼ4-1ƫ����ʵ��ģ��
��I-DEAS�ļ���ʵ��ģ�ʹ��䵽����Ԫ���������С��ڴ˼���ģ�͵Ļ����ϣ�����Բ����ÿ360��/5һ���ڵ���еȷ֣�ѡ��ƽ�������ε�Ԫ���Զ�������4-2��ʾ������Ԫ����ͼ��
����ƫ�������������ֱ������һ�𣬲�ͨ��������Ť�أ�����ƫ�������ʱ����ȡƫ�****���Ӵ����ڵ㷨��λ�ƣ��Լ�ƫ������Բ����Ӵ������ڵ�ľ���λ��Ϊ�㣨��ͼ4-2��ʾ����
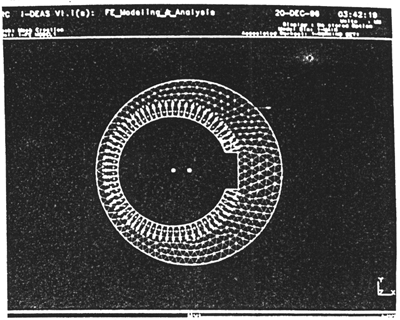
ͼ4-2ƫ��������Լ��ͼ
�ݰ���ͨ����н���������ƫ������Բ���ϣ������ڲ�ͬ�Ĺ�����Ӵ��㲻��ͬ����ˣ�����ƫ�������ϵ������ʱ����Ҫ����Բ���ϵ�ÿ���ڵ㣬���μӵ�λ�غɣ��������Բ����ÿ���ڵ��λ�ƣ��������ϵ��ֵ��������Щ���ϵ��ֵ�������ʺϼ�����õĴ����ļ�PXTRD.DAT��
4.3.2���dzݰ������Ԫ��ȼ���
���dzݰ����ڳ����Ǵ����У�����˫�������������ˣ������ٳݲ�����ڳ��֣��Ǵ����˶��������Ĺؼ�������ݰ�һ�㶼��ֱ��Բ�����֡������������Ӵ����õ�������ƽ���ڳݰ�ƽ�������Ⱦ����ġ��ڰ��������κ��������ã���˿�����Ϊ���ڸ��������Ӧ��������������Z����ֱ�ڰ��ţ��ķ�����Ϊ�㣬���Ц�z=��yz=��xz=0,ʣ�µ�����������x��y��xy���������ں�XOYƽ
����ƽ�е�ƽ���ڡ����dzݰ��ʵ��ģ����ͼ4-3��ʾ�����������ѶԳݰ���о���ƽ��Ӧ��������������
���dzݰ��ʵ��ģ����ͼ4-3��ʾ�����䴫�䵽����Ԫģ���У���ƽ�������ε�Ԫ�������֣���ͼ4-4��ʾ����������ܱ߽ڵ���Ϊ360��/Z2��
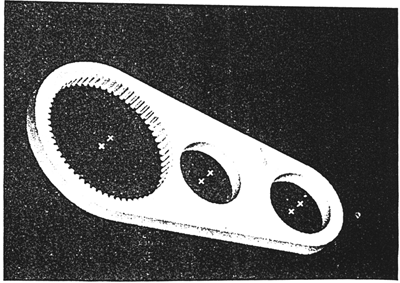
ͼ4-3�ݰ�ʵ��ģ��
�������ڳ��г��ִ������������У���������������õ�֮������λ�ƣ���ˣ��ڶԳݰ���и���λ��Լ��ʱ��Լ��ˮƽλ�ƵĽڵ�Ӧ������ѡ���������õ�֮���ˮƽ���귶Χ֮�⡣Լ��Ǧ��λ�ƵĽڵ�Ӧ������ѡ���������õ�֮��Ĵ�ֱ����֮�⡣�����Ų���������Լ���ڵ�����ķ���Ӱ���������õ�֮������λ�ơ��������ԭ����ݰ�����˱�Եһ�ڵ��ˮƽλ��Ϊ�㣬�������ݰ�ĸ���ˮƽλ�ƣ���ݰ����϶˱�Եһ�ڵ㼰�п״�ֱ�Գ�����ݰ����ϱ߱�Ե����Ľڵ�λ��Ϊ�㣬�������ݰ�ĸ��崹ֱλ�ƺ����λ�ƣ���ͼ4-4 ��ʾ��
ͼ4-4�ݰ����缰Լ��ͼ
��λ�غ����μ��ڸ����������Բ�ܱ߸��ڵ㣬�Լ�����������ϵ��ڳ�Ȧ�ֶ�Բ�ڵ��ϣ������������ϵ����Ϊ�����ᡢ�ڳ�Ȧ�����࣬�ֱ�������ļ�GF1.DAT,GF2.DAT��GFN.DAT��GFN.DAT�ȡ�
4.4ƫ�������dzݰ��λ�Ƽ���ն�ϵ��
������Ԫ�������ƫ���ͳݰ�����ϵ�����Ϳ�����ʽ��4-12��д�������ڲ�ͬ����ʱ������������������������Ľڵ���ȷ����顣���ǣ���������ø�ƫ�����ݰ������ķ��������������ܱ߷Ǿ����仯�ģ��������÷�Χ���Ӵ��ǣ�Ҳ��֪��������������������ܴ�����ѡ�����б�Ҫ��������ø�����������Ľڵ��غɼ��Լ��
4.4.1����غɵĴ���

ȷ�������ڽṹ�߽��ϵķǾ����غ���һ�����ӹ�����������Ҫ����һЩ�ϸ��ӵļ��㣬Ʃ����ýӴ���������Ԫ�����м��㡣��ʵ��Ӧ���г�����һЩ���Ƶļ��������������Щ���ӵ�δ֪�ֲ����ɡ���������غɣ�һ��������ܱ߰����ҹ��ɷֲ���ͼ4-5��ʾ����
P��= P�� maxcos K�� ��4-20��
ʽ��P����Ϊ�ֲ��غɣ�
P�� max Ϊ���ֲ��غɣ�
����ʽ��д��
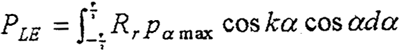
���ǵõ�
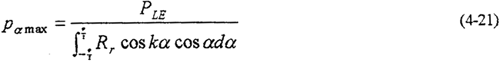
����PLEΪ��и��ɵĺ�����
RrΪƫ����ݰ�װ뾶��
��Ϊ�Ӵ��ǡ�
ϵ��K�ɰ���ʽ����
����=��/2ʱ����ʽ��4-20����֪P��Ϊ�㣺��P��=P�� maxcosK��=0

���ֲ���������Ժ��ɰ���ʽ����Ӵ��߽��ϸ��ڵ�֮�����Ϸֲ����ĺ���Pm����X��Y�᷽���ϵķ���Pmx��Pmy

Ȼ������ѧ��Чԭ���������ϵĺ�����������ֱ����õ���Ӧ�ı߽���ڵ��ϡ���߽��ϸ��ڵ�֮�����һ��϶̣�����Ϊ�����ϵ��������������ηֲ�����Pmx��Pmy�Ϳ�����Ϊ�����������ε������ϣ�ͼ4-6��a������
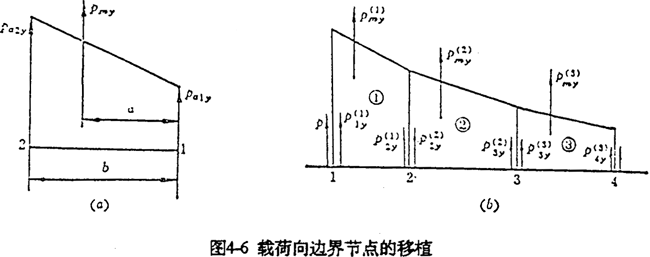
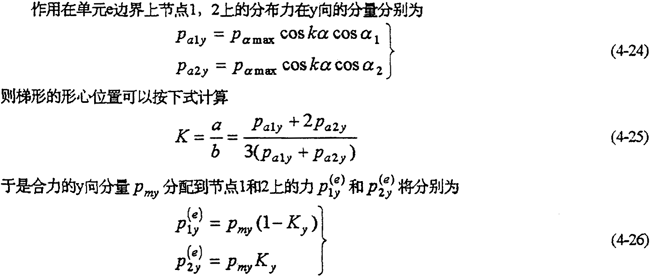
���ڱ߽���ÿһ���Σ�������������������ٶ�ÿһ���߽�㴦������ͼ��õ��߽�ڵ���y����غɷ�����ͼ4-6��b���������磬���ڱ߽�ڵ�2����ڵ��غ�P2yΪ

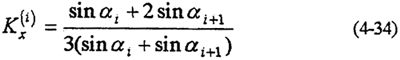
�ڼ����У��Ӵ��ǦյĴ�С��Ԥ�ȸ����ģ����Ĵ�С��Ӵ����ĸնȡ���϶�Լ�������������йء�һ������£���120�㡫180�㷶Χ��ѡȡ�����ĽӴ���ȡ��=150����㡣
��һҳ
��һҳ