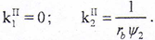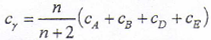第四章 鼓形齿联轴器啮合分析和力分析
从加工方法和运行状态所确定的内外齿轮齿面的空间关系来看,鼓形齿联轴器可分为共轭齿面和非共轭齿面两种。用双分齿切齿法加工出的鼓形齿轮[116],与直齿内齿轮在设计的轴间倾角下啮合就是共轭状态的鼓形齿联轴器传动,而与直齿内齿轮在不同于设计轴间倾角下啮合时,内外齿轮齿面却是处于非共轭状态的。以非内外齿轮共轭切齿法加工出的鼓形齿轮,无论处于何种安装角度,内外齿轮齿面都是非共轭状态的。
鼓形齿联轴器具有复杂的运动学机理和力学特性,以往这些方面的研究[68~73][76][79~82][84][85]都存在一定的片面性。本章将系统地对这一问题进行深入讨论。
4.1 内外齿轮齿面方程的建立
要进行鼓形齿联轴器的啮合分析和力分析,首先必须创建鼓形齿联轴器内外齿轮齿面的几何数学模型,也就是要建立内外齿轮齿面的方程。
4.1.1 共轭齿面方程
共轭齿面方程可由前一章的弹性共轭齿面数值解给出,但由于离散的数值曲面会给分析计算带来较大困难,而啮合过程是变形后的变形基本曲面起作用,由前面的分析计算知,对于单对齿啮合过程,变形基本曲面求解与传统的刚性共轭曲面求解是相同的。本章将给出内外齿轮齿面解析方程,进行啮合分析和力分析。
1.坐标系及坐标变换
坐标系如图3-2所示,其坐标系空间关系及坐标变换关系由3.3.4.1给出。
2.内齿轮齿面方程
内齿轮为直齿,其端面齿形及坐标关系如图3-3所示。设端面齿廓线为渐开线,xc2坐标通过渐开线在基圆上的起点,(o,xc2,yc2,zc2)坐标下的齿面方程为

式中 ψ2——齿面参变量,设α2为齿面某一点K处的压力角,则有ψ2=tgα2。
rb——渐开线基圆半径。
将(4-1-1)式转换到S2坐标系,方程为
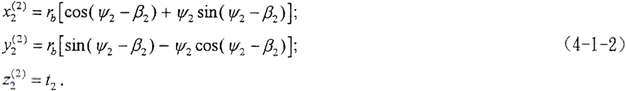
将(4-1-3)式转换到S20坐标系,方程为

式中 β2——内齿轮基圆齿槽宽所对圆心角之半。
β2=π/(2z)+(2xr2tgα+xτ2)/z+tgα-α
式中 α——分度圆压力角
xr2——内齿轮径向变位系数
xτ2——内齿轮切向变位系数
(4-1-3)式就是内齿轮齿面在S20系的齿面方程。
3.与内齿轮齿面共轭的外齿轮齿面方程
根据求解共轭齿面的运动学法[2],外齿轮齿面方程为
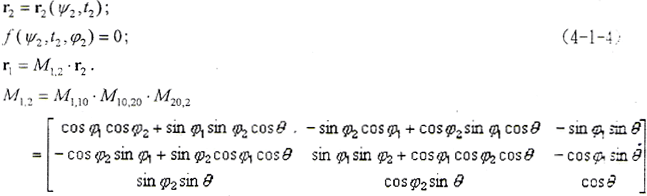
f(ψ2,t2,φ2)=0为啮合方程,为由n·v(12)=0推导而来。
在(o,x2,y2,z2)坐标系,内轮齿齿面法向矢量的三个坐标分量为

在(o,x2,y2,z2)坐标系,相对速度的三个坐标分量为
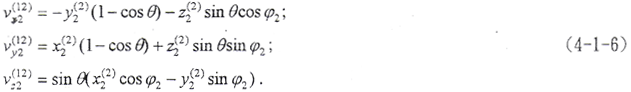
将(4-1-5)、(4-1-6)式代入n·v(12)=0,得
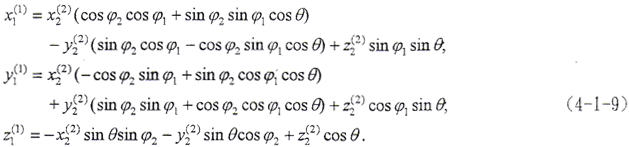
(4-1-9)式中,φ1、φ2为二齿面的转角,令φ1=φ2=φ,将(4-1-2)式及由(4-1-8)式解出的t2代入(4-1-9)式,即可得到以ψ2、φ为参变量的外齿轮齿面方程。
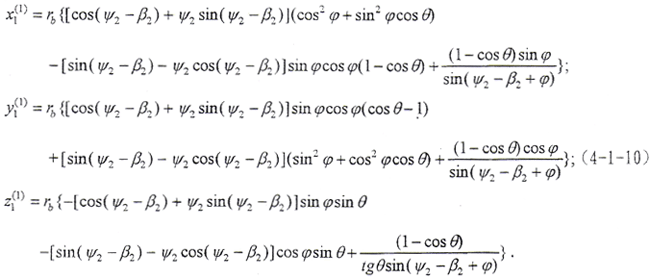
为了啮合分析方便,要给出在固定坐标系下的接触线方程,即啮合面方程。在S20上接触线方程为
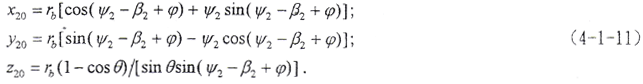
(4-1-11)式就是啮合面方程。
由f(ψ2,t2,φ2)=0,r2=r2(ψ2,t2)可以给出内齿轮齿面上的接触线方程
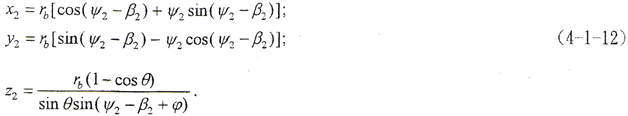
4.1.2 与内齿轮齿面非共轭的外齿轮齿面方程
外齿轮齿面及坐标系如图4-1所示。此处只讨论在平行于端面的各截面上,为不同变位系数的渐开线外齿轮。
设中截面齿廓为渐开线,xc1坐标轴线通过渐开线在基圆上的起点,(o,xc1,yc1,zc1)坐标下的齿面方程为

式中 ψ1、t1——齿面参变量,设α1为齿面某一点k1处的压力角,则ψ1=tgα1。
rb——渐开线基圆半径
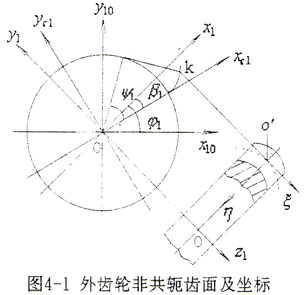
(4-1-13)式进行坐标变换得到S1坐标系下的方程。
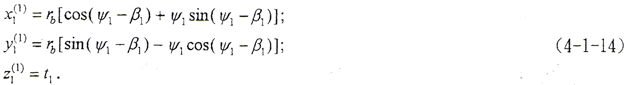
β1为外齿轮基圆齿厚所对圆心角之半,
β1=π/(2z)+(2xr1tgα+xτ1)/z+tgα-α+△
式中 α——分度圆压力角;
xr1——外齿轮径向变位系数;
xτ1——外齿轮切向变位系数;
△——鼓形引起的径向变位的差角
△的计算如下,设鼓形齿鼓度曲线为一椭圆,参数为长半轴a,短半轴b,当a=b时为圆弧。在鼓度曲线上建立局部坐标系(o′,ξ,η),o′为齿宽中线与分度圆线交点,ξ与z1方向相同,η为指向齿轮轴线的方向。在此坐标系上椭圆方程为
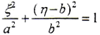
设齿宽为B,则a>B/2。在靠近原点o′的半弧上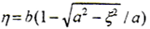 。因ξ与z1方向相同,以t1为参变量,则
。因ξ与z1方向相同,以t1为参变量,则
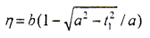
这就是由鼓形引起的径向变位的负变位量,故
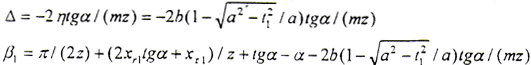
将(4-1-4)式转换到S10系中有
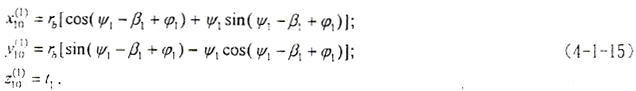
为了后面啮合分析方便,再将(4-1-15)式转换到S20系
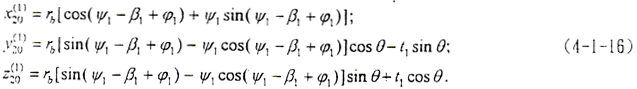
4.2 鼓形齿联轴器啮合分析
4.2.1 共轭齿面啮合分析
1.接触线
由(4-1-10)式和式(4-1-12)式通过计算,可以得到内外齿轮齿面上接触线坐标,由计算出的坐标值即可绘出接触线图形。
式中ψ要求:ψf≤ψ≤ψa,其中ψa=tgαa,ψf=tgαf;αa、αf为内齿轮轮齿顶和齿根压力角。
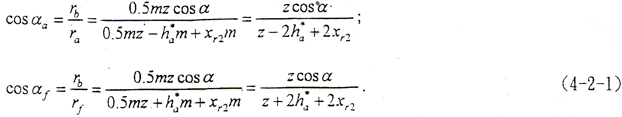
以m=3mm,z=56,θ=1.5°,xr1=xr2=0,ha*=1,齿宽按需要取到足够大为例计算,确定-90°≤φ≤270°期间的若干条接触线。由建立的齿面方程所决定,φ=0时,齿面处于纯翻转位置。由式(4-2-1)计算得αa=12.968°,αf=24.866°
通过计算,得到内外齿轮齿面接触线坐标,表4-1、表4-2给出部分坐标值计算结果。图4-2所示为φ间隔2.5°,内外齿轮齿面转过一圈的齿面接触线。
表4-1 外齿轮齿面接触线坐标(m=3mm z=56 α=20° θ=1.5° xr1=xr2=0 ha*=1)
| φ(°) |
α1(°) |
z1(mm) |
x1(mm) |
φ(°) |
α1(°) |
z1(mm) |
x1(mm) |
| -10.0 |
12.968
15.785
18.526
21.181
23.745 |
80.313
15.406
8.358
5.666
4.252 |
81.305
82.046
83.246
84.653
86.241 |
170.0 |
12.968
15.785
18.526
21.181
23.745 |
-80.310
-15.406
-8.358
-5.666
-4.252 |
81.305
82.046
83.246
84.653
86.241 |
| 10.0 |
12.968
15.785
18.526
21.181
23.745 |
3.204
2.863
2.607
2.412
2.263 |
80.924
81.963
83.196
84.616
86.212 |
190.0 |
12.968
15.785
18.526
21.181
23.745 |
-3.204
-2.863
-2.607
-2.412
-2.263 |
80.924
81.963
83.196
84.616
86.212 |
| 30.0 |
12.968
15.785
18.526
21.181
23.745 |
2.571
2.501
2.449
2.413
2.392 |
80.911
81.949
83.182
84.602
86.197 |
210.0 |
12.968
15.785
18.526
21.181
23.745 |
-2.571
-2.501
-2.449
-2.413
-2.392 |
80.911
81.949
83.182
84.602
86.197 |
| 50.0 |
12.968
15.785
18.526
21.181
23.745 |
2.754
2.746
2.749
2.762
2.785 |
80.899
81.936
83.169
84.588
86.182 |
230.0 |
12.968
15.785
18.526
21.181
23.745 |
-2.754
-2.746
-2.749
-2.762
-2.785 |
80.899
81.936
83.169
84.588
86.182 |
| 70.0 |
12.968
15.785
18.526
21.181
23.745 |
3.009
3.029
3.058
3.096
3.142 |
80.888
81.925
83.157
84.576
86.170 |
250.0 |
12.968
15.785
18.526
21.181
23.745 |
-3.009
-3.029
-3.058
-3.096
-3.142 |
80.888
81.925
83.157
84.576
86.170 |
表4-2 内齿齿面接触线坐标(m=3mm z=56 α=20° θ=1.5° xr1=xr2=0 ha*=1)
| φ(°) |
α2(°) |
z2(mm) |
x2(mm) |
φ(°) |
α2(°) |
z2(mm) |
x2(mm) |
| -10.0 |
12.968
15.785
18.526
21.181
23.745 |
161.607
31.725
17.616
12.216
9.370 |
80.938
81.975
83.207
84.627
86.221 |
170.0 |
12.968
15.785
18.526
21.181
23.745 |
-161.602
-31.725
-17.616
-12.216
-9.370 |
80.938
81.975
83.207
84.627
86.221 |
| 10.0 |
12.968
15.785
18.526
21.181
23.745 |
5.839
5.135
4.594
4.167
3.821 |
80.938
81.975
83.207
84.627
86.221 |
190.0 |
12.968
15.785
18.526
21.181
23.745 |
-5.839
-5.135
-4.594
-4.167
-3.821 |
80.938
81.975
83.207
84.627
86.221 |
| 30.0 |
12.968
15.785
18.526
21.181
23.745 |
3.168
2.990
2.838
2.709
2.597 |
80.938
81.975
83.207
84.627
86.221 |
210.0 |
12.968
15.785
18.526
21.181
23.745 |
-3.168
-2.990
-2.838
-2.709
-2.597 |
80.938
81.975
83.207
84.627
86.221 |
| 50.0 |
12.968
15.785
18.526
21.181
23.745 |
2.369
2.305
2.250
2.203
2.164 |
80.938
81.975
83.207
84.627
86.221 |
230.0 |
12.968
15.785
18.526
21.181
23.745 |
-2.369
-2.305
-2.250
-2.203
-2.164 |
80.938
81.975
83.207
84.627
86.221 |
| 70.0 |
12.968
15.785
18.526
21.181
23.745 |
2.094
2.079
2.070
2.067
2.069 |
80.938
81.975
83.207
84.627
86.221 |
250.0 |
12.968
15.785
18.526
21.181
23.745 |
-2.094
-2.079
-2.070
-2.067
-2.069 |
80.938
81.975
83.207
84.627
86.221 |
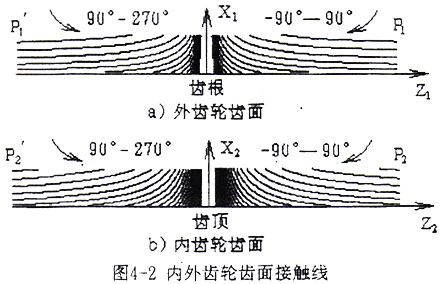
φ在-90°≤φ≤90°范围变化时,从-90°至小于0°的某一角度范围,内外齿轮齿面无接触线;此后,接触线在内外齿轮齿面中截面的右外侧从外齿轮齿顶P1和内齿轮齿根P2进入,逐渐向齿宽中截面位置移动,在小于90°的某一角度结束,接触线弯曲方向及倾斜方向如图4-2所示。开始进入接触和最后脱离接触时的φ值由齿轮参数决定。φ在90°≤φ≤270°范围变化时,接触线在内外齿轮齿面中截面的左外侧P1′、P2′啮入,转角位置与右外侧啮合对称。内外齿轮齿面左右两侧的接触线呈与X1、X2坐标对称形状。
2.齿形分析
通过对齿面分度圆柱截面线和端截面线的分析可进一步了解其齿形特点。由(4-1-10)式,设r为分度圆半径,给定x12+y12=r2,可解出齿面分度圆柱截面线的坐标值,将z1oy1平行平面内的点以足够的密度连接成曲线,就得到分度圆柱上的齿厚线在z1oy1平面上的投影,即得到齿宽方向的齿形曲线。以上例给出的参数,计算绘制的鼓形齿齿宽方向的齿形曲线如图4-3所示。
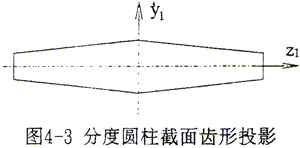
由图看出,轮齿沿齿宽方向齿厚是变化的,在靠近中截面附近,截线为一近似圆弧,离开中截面越远,截线越呈直线形状,整个齿形为与y1轴对称鼓形。同样,可以由(4-1-10)式取z1为某一常数,求出x1oy1的截面线坐标。通过计算发现各位置端截面齿形为一近似渐开线,在中截面处与渐开线最逼近。由此可知,与渐开线直齿内齿轮共轭的外齿轮为一轴向变齿厚的、端截面为近似渐开线齿形的齿轮。
3.诱导法曲率及齿面曲率干涉校验
设内齿轮齿面为ΣⅠ,外齿轮齿面为ΣⅡ。诱导法曲率是指两齿面ΣⅠ、ΣⅡ上沿同一切线方向的法曲率kⅠ与kⅡ之差,kⅠⅡ=kⅠ-kⅡ。如果规定两齿面接触点处的公法线矢量n的方向为由齿面ΣⅠ的实体指向空域,则其诱导法曲率必须为负值,才不会发生曲率干涉,两齿面才能正常啮合;反之若为正值,则会发生曲率干涉,两齿面不能正常啮合。
诱导法曲率在两个互相垂直的切线方向上的值之和为定值。对于线接触啮合,因为在接触线方向两齿面的法曲率相等,即kτⅠⅡ=0,则诱导法曲率两个主方向之一与接触线方向重合。另一个主方向即对应于kⅠⅡ的绝对值最大方向,与接触线方向垂直。
设ΣⅠ的主方向为iⅠ、iⅡ,其两个主值为k1Ⅰ、k2Ⅰ,ΣⅡ在iⅠ方向的法曲率为k1Ⅱ(1),在iⅡ方向的法曲率为k2Ⅱ(1)。由啮合原理分析推导知[5]
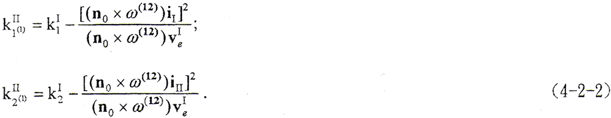
式中 n0——法线单位矢量
ω(12)——相对角速度矢量
veⅠ——ΣⅠ的牵连运动速度矢量
由(4-1-3)式可计算出

式中 ψ2=tgα2。
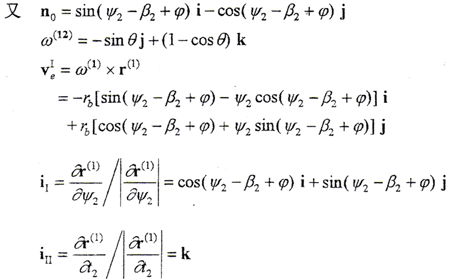
将以上求出的n0、ω(12)、veⅠ、iⅠ、iⅡ及(4-2-3)式代入(4-2-2)式,即可解得
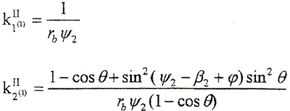
设垂直于接触线切线方向的诱导法曲率为kσⅠⅡ,则有
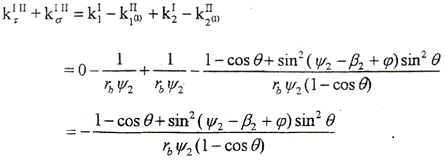
由kτⅠⅡ=0,得
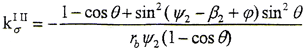
由于|cosθ|≤1,ψ2≥0
所以
kσⅠⅡ≤0
与kτⅠⅡ夹角为q的任一方向诱导法曲率为
kⅠⅡ=kτⅠⅡcos2q+kσⅠⅡsin2q=kσⅠⅡsin2q
显然,kⅠⅡ≤0。
由此推知共轭齿面鼓形齿联轴器内外齿轮齿面无曲率干涉。
外齿轮轴线与内齿轮轴线的轴间倾角小于θ安装时,设轴间倾角为θ′,则在iⅠ、iⅡ方向上外齿轮齿面两法曲率为
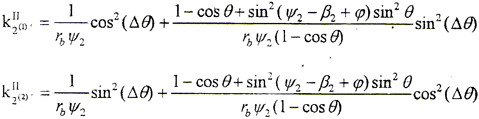
式中 △θ=θ-θ′
iⅠ、iⅡ方向上的诱导法曲率为
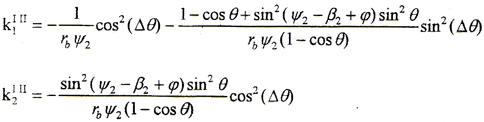
显然,k1ⅠⅡ≤0,k2ⅠⅡ≤0,不会发生曲率干涉。
4.相对滑动系数
由啮合原理推导知[5],齿面滑动系数为

式中 kvⅠ——齿面ΣⅠ上参考点的相对运动速度矢量v(12)方向的法曲率。
由Euler公式知,kvⅠ=k2Ⅰcos2qv+k1Ⅰsin2qv
式中 qv——相对运动速度矢量与主方向iⅡ的夹角
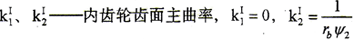
所以有kvⅠ=k2Ⅰcos2qv
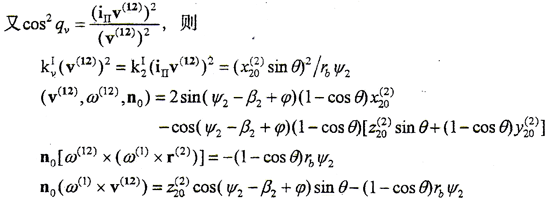
将以上求出的各量代入(4-2-4)式,得
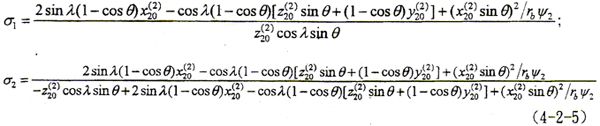
关于齿面ΣⅠ、ΣⅡ的滑动系数表达式(4-2-5)较复杂,为了便于分析,分别以参数φ、ψ2、t2为变量,计算出σ1、σ2的若干组数据,由表4-3给出。
表4-3 滑动系数计算数据(m=3mm z=56 α=20° xr1=0 xr2=0 θ=1.5°)
| φ=0° t2=1mm |
φ=0° t2=11mm |
φ=0° t2=21mm |
φ=0° t2=31mm |
| ψ2(°) |
σ1 |
σ2 |
ψ2(°) |
σ1 |
σ2 |
ψ2(°) |
σ1 |
σ2 |
ψ2(°) |
σ1 |
σ2 |
3.00
6.00
9.00
12.00
15.00
18.00
21.00
24.00 |
9.518
20.077
13.782
10.780
9.102
8.093
7.477
7.114 |
1.026
1.052
1.078
1.102
1.123
1.141
1.154
1.163 |
3.00
6.00
9.00
12.00
15.00
18.00
21.00
24.00 |
3.592
1.825
1.253
0.979
0.827
0.735
0.679
0.646 |
1.385
2.212
4.958
-48.30
-4.785
-2.780
-2.119
-1.829 |
3.00
6.00
9.00
12.00
15.00
18.00
21.00
24.00 |
1.881
0.955
0.656
0.513
0.433
0.385
0.356
0.338 |
2.134
-21.599
-1.907
-1.053
-0.764
-0.626
-0.552
-0.512 |
3.00
6.00
9.00
12.00
15.00
18.00
21.00
24.00 |
1.274
0.647
0.444
0.347
0.293
0.261
0.241
0.229 |
4.641
-1.836
-0.799
-0.532
-0.415
-0.353
-0.317
-0.297 |
| φ=30° t2=1mm |
φ=30° t2=11mm |
φ=30° t2=21mm |
φ=30° t2=31mm |
| ψ2(°) |
σ1 |
σ2 |
ψ2(°) |
σ1 |
σ2 |
ψ2(°) |
σ1 |
σ2 |
ψ2(°) |
σ1 |
σ2 |
3.00
6.00
9.00
12.00
15.00
18.00
21.00
24.00 |
37.202
20.029
14.545
12.009
10.677
9.975
9.662
9.628 |
1.027
1.052
1.074
1.090
1.103
1.111
1.115
1.116 |
3.00
6.00
9.00
12.00
15.00
18.00
21.00
24.00 |
3.382
1.820
1.322
1.091
0.970
0.906
0.878
0.875 |
1.420
2.219
4.106
11.939
-32.722
-9.696
-7.204
-6.999 |
3.00
6.00
9.00
12.00
15.00
18.00
21.00
24.00 |
1.771
0.953
0.692
0.571
0.508
0.475
0.460
0.458 |
2.297
-20.482
-2.250
-1.334
-1.033
-0.904
-0.851
-0.846 |
3.00
6.00
9.00
12.00
15.00
18.00
21.00
24.00 |
1.200
0.646
0.469
0.387
0.344
0.321
0.311
0.310 |
6.006
-1.823
-0.883
-0.631
-0.525
-0.474
-0.452
-0.450 |
| φ=60° t2=1mm |
φ=60° t2=11mm |
φ=60° t2=21mm |
φ=60° t2=31mm |
| ψ2(°) |
σ1 |
σ2 |
ψ2(°) |
σ1 |
σ2 |
ψ2(°) |
σ1 |
σ2 |
ψ2(°) |
σ1 |
σ2 |
3.00
6.00
9.00
12.00
15.00
18.00
21.00
24.00 |
25.139
15.119
12.295
11.430
11.562
12.520
14.517
18.368 |
1.041
1.070
1.088
1.096
1.095
1.087
1.074
1.058 |
3.00
6.00
9.00
12.00
15.00
18.00
21.00
24.00 |
2.285
1.374
1.117
1.039
1.051
1.138
1.319
1.669 |
1.778
3.672
9.516
26.807
20.683
8.255
4.130
2.494 |
3.00
6.00
9.00
12.00
15.00
18.00
21.00
24.00 |
1.197
0.720
0.585
0.544
0.550
0.596
0.691
0.874 |
6.082
-2.567
-1.411
-1.193
-1.224
-1.474
-2.236
-6.957 |
3.00
6.00
9.00
12.00
15.00
18.00
21.00
24.00 |
0.811
0.487
0.396
0.368
0.373
0.404
0.468
0.592 |
-4.280
-0.951
-0.656
-0.583
-0.594
-0.677
-0.880
-1.452 |
| φ=90° t2=1mm |
φ=90° t2=11mm |
φ=90° t2=21mm |
φ=90° t2=31mm |
| ψ2(°) |
σ1 |
σ2 |
ψ2(°) |
σ1 |
σ2 |
ψ2(°) |
σ1 |
σ2 |
ψ2(°) |
σ1 |
σ2 |
3.00
6.00
9.00
12.00
15.00
18.00
21.00
24.00 |
-17.178
-2.016
-0.967
-0.602
-0.412
-0.289
-0.198
-0.125 |
0.945
0.668
0.492
0.376
0.292
0.224
0.165
0.111 |
3.00
6.00
9.00
12.00
15.00
18.00
21.00
24.00 |
-1.562
-0.184
-0.088
-0.055
-0.038
-0.027
-0.018
-0.012 |
0.610
0.155
0.081
0.052
0.036
0.026
0.018
0.012 |
3.00
6.00
9.00
12.00
15.00
18.00
21.00
24.00 |
-0.818
-0.096
-0.046
-0.029
-0.020
-0.014
-0.010
-0.006 |
0.450
0.088
0.044
0.028
0.020
0.014
0.010
0.006 |
3.00
6.00
9.00
12.00
15.00
18.00
21.00
24.00 |
-0.555
-0.065
-0.032
-0.020
-0.014
-0.010
-0.007
-0.004 |
0.357
0.061
0.030
0.019
0.013
0.010
0.007
0.004 |
分析表4-3的数据,可以得出以下结论:
(1)φ、ψ2不变的情况下,t2增加,σ1的绝对值减小,即在内齿轮齿面相同的周向和径向位置上,越远离齿宽中截面,滑动系数越小;
(2)φ、t2不变的情况下,ψ2增加,在大部分周向位置上σ1的绝对值减小,即越往内齿轮齿根,滑动系数越小;
(3)ψ2、t2不变的情况下,σ1的变化情况较复杂,不同的周向位置变化范围,σ1的增大或减小趋势不同;
(4)外齿轮齿面滑动系数σ2的变化较复杂,当经历σ1大于1变为σ1小于1的过程,必然出现σ2→∞的情况。在不同周向位置和轴向位置,对ψ2进行一维搜索计算,求解出σ2→∞的点,如表4-4所给。由数据可以看出,外齿轮齿面最大滑动系数点,在不同周向位置和轴向位置,出现于不同的齿高位置。
表4-4 外齿轮齿面最大滑动系数点参数
(m=3mm z=56 α=20° xr1=0 xr2=0 θ=1.5°)
| φ(°) |
t2(mm) |
ψ2(°) |
φ(°) |
t2(mm) |
ψ2(°) |
0.000
0.000
0.000
30.000 |
11.000
21.000
31.000
11.000 |
11.543
5.704
3.829
13.803 |
30.000
30.000
60.000
60.000 |
21.000
31.000
21.000
31.000 |
5.653
3.649
23.779
25.879 |
5.重合度
由前面分析的齿面接触线状况知,一对齿面在一周运动中不是始终连续啮合的,它们在一周中从开始进入啮合到脱离啮合所转过的角度与一个齿距角之比为重合度。重合度反映了齿轮啮合过程中同时啮合齿对数的多少,是一个重要的啮合特性。以下分析计算共轭齿面鼓形齿联轴器的重合度。
根据接触线的分析知,啮合点在内齿轮齿面齿根处远离中截面的位置,啮出点在内齿轮齿面齿顶上靠近中截面的位置。由(4-1-12)式的第三式
z2=rb(1-cosθ)/[sinθsin(ψ2-β2+φ)]
解得

在啮入点ψ2=tgαf,z2=B/2,αf为内齿轮齿根压力角,B为齿宽,设啮入点φ=φei,
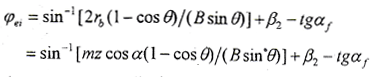
在啮出点ψ2tgαa,此时z2为不等于零的最小值,即取
sin(ψ2-β2+φ)=1,故有

αa为内齿轮齿顶压力角,设啮出点φ=φeo,
φeo=π/2+β2-tgαa
αf、αa由(4-2-1)式计算。设单齿啮合转角为φe,则有
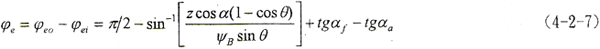
式中 ψB=B/m为齿宽系数。
齿距角为2π/z,由于一对齿面在齿轮转一转中有两次啮入啮出,所以重合度
ε=φez/π (4-2-8a)
将(4-2-7)式和(4-2-1)式代入(4-2-8a)式中,且 ,所以
,所以
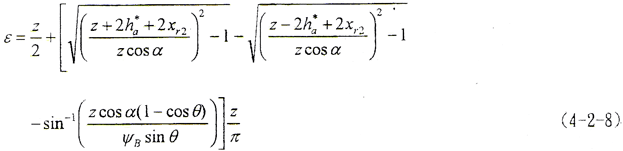
以m=3mm,z=56,ha*=1,xr1=xr2=0,α=20°,θ=1.5°代入(4-2-8)式,得ε=30.928,即56对齿中有时有30对齿、有时有32对齿同时啮合,分别占总齿数的54%和57%.可见共轭齿面鼓形齿联轴器具有较高的啮合重合度。
由(4-2-8)式知,共轭齿面鼓形齿联轴器重合度与齿数、齿宽系数、齿高系数、径向变位系数、压力角和轴间倾角有关。图4-4给出了ε-θ、ε-ψB、ε-z、ε-xr、ε-ha*和ε-α关系曲线。


(a)ε-θ关系(z=56 α=20° ψB=12 ha*=1 Xr2=0)
(b)ε-ψB关系(θ=1.5° z=56 α=20° ha*=1 Xr2=0)
(c)ε-z关系(θ=1.5° α=20° ψB=12 ha*=1 Xr2=0)
(d)ε-Xr2关系(θ=1.5° z=56 α=20° ψB=12 ha*=1)
(e)ε-ha*关系(θ=1.5° z=56 α=20° ψB=12 Xr2=0)
(f)ε-α关系(θ=1.5° z=56 ψB=12 ha*=1 Xr2=0)
由图4-4知,重合度随轴间倾角、径向变位系数和分度圆压力角的增大单调减小,随齿宽系数、齿数和齿顶高系数的增大单调增加。重合度随齿宽系数的增大有较大的非线性,当齿宽系数增大到14之后,重合度增加很小,因此不宜盲目以增加齿宽系数来增加重合度。重合度的增加量约为齿数增加量的50%,因此,应尽可能地增大齿数来增加重合度。其他参数在合理的取值范围内变化时,重合度变化较小。
4.2.2 非共轭齿面啮合分析
非共轭齿面啮合为点接触,此处只讨论圆弧及椭圆弧鼓度曲线鼓形齿联轴器的非共轭齿面啮合。
1.接触分析
根据非共轭曲面的啮合条件[2]

rⅠ=rⅡ有三个坐标分量的标量方程;nⅠ=nⅡ的三个坐标分量两两成比例,有两个标量方程。共有五个独立的标量方程。
内外齿轮齿面在固定坐标系S20下的方程由(4-1-3)式及(4-1-16)式给出。
设内齿轮为主动件,转角φ2给定,并令△φ=φ2-φ1,则在齿面ΣⅠ、ΣⅡ中ψ1、ψ2、t1和t2为参变量,加上运动参变量△φ,共有五个未知量。这样,五个方程有五个未知量,方程可解。
内齿轮齿面法线矢量的计算:
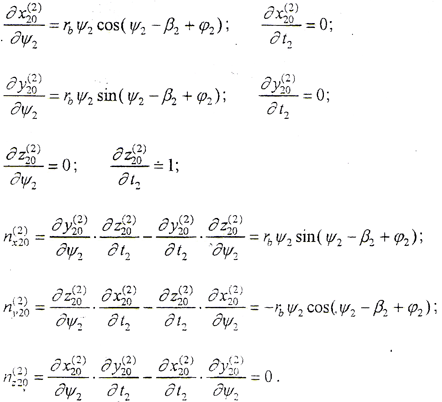
外齿轮齿面法线矢量的计算:
对于圆弧鼓度曲线,设鼓度半径为rg,β1表达式中,a=b=rg。
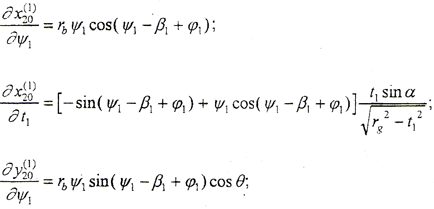
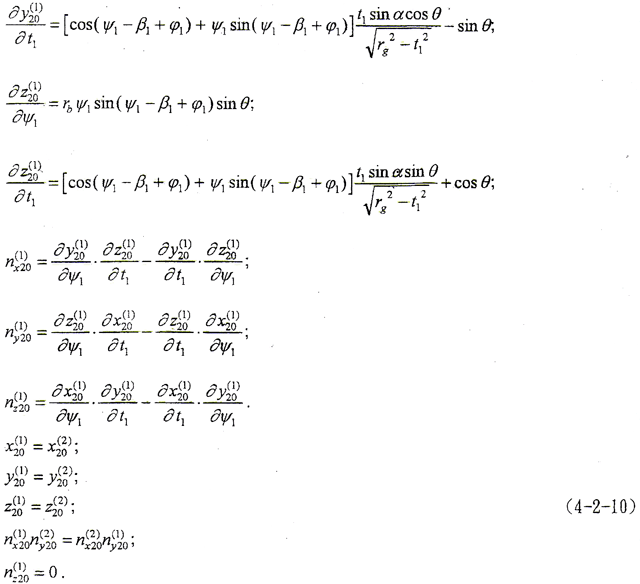
(4-2-10)式为一非线性方程组,由于此方程组较复杂,很难求得解析解,必须寻求其数值解。现运用优化原理[117]求解接触点的数值解。
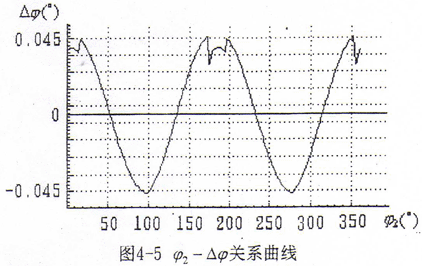
将方程写成优化标准形式
Fi(X)=0 (i=1,2,3,4,5),X={ψ1,ψ2,t1,t2,△φ};目标函数为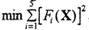 ,约束条件为tgαf1≤ψ1≤tgαa1,tgαa2≤ψ2≤tgαf2,其中αf1、αf2和αa1、αa2为鼓形外齿轮及直齿内齿轮的齿根圆压力角和齿顶圆压力角。
,约束条件为tgαf1≤ψ1≤tgαa1,tgαa2≤ψ2≤tgαf2,其中αf1、αf2和αa1、αa2为鼓形外齿轮及直齿内齿轮的齿根圆压力角和齿顶圆压力角。
给定一系列的φ2值(0~2π),间隔为某一设定的角度,可算得各个点的α1、α2、t1、t2及△φ的数据值。表4-5给出了0°≤φ2≤360°,间隔为15°的一组数据值,由此数据表即可进行啮合点分析。改变轴间倾角θ和鼓度曲线参数a、b进行若干次计算,还可进行对比分析。
表4-5 α1、α2、t1、t2、△φ的计算结果
(m=3mm,z=56,α=20°,rg=131mm,θ=1.5°)
| φ2(°) |
α1(°) |
α2(°) |
t1(mm) |
t2(mm) |
△φ(°) |
| 0.000 |
21.440361 |
21.450669 |
9.393189 |
9.338940 |
0.037091 |
| 15.000 |
13.098483 |
12.967874 |
8.997373 |
9.466054 |
0.036430 |
| 30.000 |
12.967874 |
12.967874 |
7.708035 |
8.694986 |
0.031671 |
| 45.000 |
12.967874 |
12.967874 |
5.910255 |
7.348820 |
0.010622 |
| 60.000 |
12.967874 |
12.967874 |
3.934636 |
5.727098 |
-0.013388 |
| 75.000 |
12.967874 |
12.967874 |
1.951379 |
3.975874 |
-0.032814 |
| 90.000 |
12.967874 |
12.967874 |
0.004159 |
2.122878 |
-0.045711 |
| 105.000 |
12.967874 |
13.036466 |
-1.911303 |
0.157252 |
-0.042695 |
| 120.000 |
12.967874 |
13.170391 |
-3.808666 |
-1.931387 |
-0.024563 |
| 135.000 |
12.967874 |
13.253320 |
-5.671477 |
-4.113668 |
0.000000 |
| 150.000 |
12.967874 |
13.257960 |
-7.410419 |
-6.278538 |
0.024339 |
| 165.000 |
12.967874 |
13.167849 |
-8.776147 |
-8.147485 |
0.040841 |
| 180.000 |
21.440342 |
21.450646 |
-9.393189 |
-9.338941 |
0.037019 |
| 195.000 |
13.098374 |
12.967874 |
-8.997380 |
-9.466062 |
0.036439 |
| 210.000 |
12.967874 |
12.967874 |
-7.708035 |
-8.694987 |
0.031671 |
| 225.000 |
12.967874 |
12.967874 |
-5.910255 |
-7.348820 |
0.010622 |
| 240.000 |
12.967874 |
12.967874 |
-3.934636 |
-5.727098 |
-0.013388 |
| 255.000 |
12.967874 |
12.967874 |
-1.951379 |
-3.975874 |
-0.033814 |
| 270.000 |
12.967874 |
12.967874 |
-0.004159 |
-2.122878 |
-0.045711 |
| 285.000 |
12.967874 |
13.036466 |
1.911303 |
-0.157252 |
-0.042695 |
| 300.000 |
12.967874 |
13.170391 |
3.808666 |
1.931387 |
-0.024563 |
| 315.000 |
12.967874 |
13.253320 |
5.671477 |
4.113668 |
-0.000000 |
| 330.000 |
12.967874 |
13.257960 |
7.410419 |
6.278539 |
0.024339 |
| 345.000 |
12.967874 |
13.167849 |
8.776147 |
8.147486 |
0.040841 |
| 360.000 |
21.440334 |
21.450638 |
9.393189 |
9.338942 |
0.037019 |
通过对多组数据进行分析,得出如下结论:
(1)当考虑实际啮合时,内齿轮齿厚减薄,使之保证足够的侧隙,数据处理后发现,△φ=0的点为对称的两点,由φ2间隔细分的数据计算可知,此两点位于偏离纯翻转区一个小角度的位置;这说明理论啮合齿对数为两对,这一结论与文献[81]所给结果是一致的;
(2)以一对齿在一转中始终啮合为例计算分析可知,△φ的变化除在纯翻转区稍有波动外,总体约呈余弦规律变化,如图4-5所示,这说明运动是非匀速的。当理论啮合齿对在△φ为零的点啮合时,与其相邻的齿对若要啮合,它的△φ值约为10-5弧度数量级;
(3)接触点在齿高方向的位置,在纯翻转区向纯摆动区转动过程中,从内外齿轮分度圆附近向外齿轮齿根部和内齿轮齿顶移动。根据齿轮的模数齿数不同,到达外齿轮齿根部和内齿轮齿顶所需转过的角度不同。在此后直至转到对面的纯翻转区的范围内,接触点都在外齿轮齿根部和内齿轮齿顶;
(4)接触点在齿宽方向的位置,在纯翻转区向纯摆动区转动过程中,从内外齿轮上距齿宽中截面远端处向齿宽中截面移动;在纯摆动区,接触点在外齿轮齿宽中截面上,由于外齿轮轴线的倾斜,此时内齿轮齿面上接触点偏离齿宽中截面一个距离,理论上为rftgθ,所算数据与此吻合。越过纯摆动区时,接触点从齿宽中截面一边移到另一边。在纯摆动区向纯翻转区转动过程中,接触点从齿宽中截面向远离齿宽中截面位置移动,直至到达最远处;
(5)啮合点处α1、α2、t1、t2、△φ关于原点对称;
(6)轴间倾角θ越小,△φmax越小;当θ=0时,t1=t2=0,此时所有齿在齿宽中截面上接触,在齿宽方向接触点不移动,承载能力最强。
2.齿面曲率分析
经求解得到内齿轮齿面的两个法曲率主值为
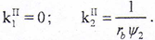
圆弧鼓度曲线外齿轮齿面的两个对应法曲率为

k1Ⅰ、k1Ⅱ的方向为齿宽方向,k2Ⅰ、k2Ⅱ的方向为齿高方向。
在齿宽方向,当rg→∞或rg/t1=cosα时,k1Ⅰ→0,对鼓形齿轮而言,这两种情况都不存在,因此总存在k1Ⅰ>k1Ⅱ,即在齿宽方向不存在曲率干涉。
在齿高方向,由于k2Ⅰ与ψ1和t1有关,是否存在在曲率干涉,需进行计算才能确定。在齿宽中截面上,k2Ⅰ=1/(rbψ1),由于内外齿轮存在轴间倾角θ,由Eular公式可计算出与k2Ⅱ同方向的外齿轮齿面法曲率,k2Ⅰ′=cos2θ/(rbψ1)。由接触点计算知,在齿宽中截面上的接触点ψ1=ψ2,因此存在k2Ⅰ′<k2Ⅱ,即说明存在曲率干涉,且θ越大,曲率干涉越严重。
在距齿宽中截面最远处的接触点,则应由t1、ψ1、ψ2代入k2Ⅰ′及k2Ⅱ计算来确定。以m=3mm,z=56,θ=1.5°为例进行计算,最远点t1=9.393mm,ψ1=tgα1=0.3927,ψ2=tgα2=0.3929,得k2Ⅰ′=0.0322289,k2Ⅱ=0.0322444,即有k2Ⅰ′<k2Ⅱ,说明同样存在曲率干涉。曲率干涉也是造成内外齿轮齿面接触点大都在外齿轮齿根部和内齿轮齿顶的根本原因。但由计算结果看出,干涉是非常轻微的,在弹性变形作用下或经跑合后即为密切接触。
4.3 鼓形齿联轴器力分析
鼓形齿联轴器与一般的内外齿轮传动相比较,因其特殊的齿面啮合接触状态和较大的啮合重合度而有较特殊的受力状态,因此有必要对其进行分析,为强度刚度设计计算及参数优化设计提供依据。
4.3.1 受力分析
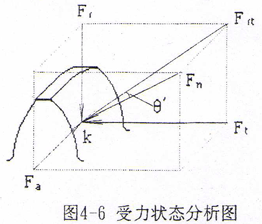
在接触点K处,受力状态如图4-6所示。作用在外齿轮轮齿K点的总作用力为Fn,Fn可分解为切向力Ft,径向力Fr和轴向力Fa。由图4-6知
Frt=Fncosθ′;Fa=Fnsinθ′。
式中θ=θcosφ;在纯翻转区,φ=0,θ′=θ;在纯摆动区φ=π/2,θ′=0;可见轴向力的大小与轮齿所处周向位置有关。当φ>π/2,θ′<0,即轴向力方向与对称点相反,它们形成绕纯摆轴线的力矩。
Ft=Frtcosαk=Fncosθ′cosαk
Fr=Frtsinαk=Fncosθ′sinαk
设联轴器作用转矩为T,对于点接触的情况,有受力平衡条件

式中n为接触点数目,Frt(i)为在第i点的端截面法向力。
对线接触的情况,有受力平衡条件

式中l为接触齿对数目,dFrt(j)为第j对齿接触线上一点的端截面法向力,sj为第j对齿的接触线。
4.3.2 啮合刚度
啮合刚度是指同时啮合的若干对轮齿在端面内轮齿总刚度的平均值。而轮齿刚度的定义是一对或若干对轮齿啮合时,单位齿宽产生单位变形所需的载荷[118]。
由于在特定的啮合位置上接触线为已知,因此可求出变形量,由求出的变形量即可求出单对齿的刚度,设单对齿刚度曲线如图4-7(a)所示。
啮合过程中,n对齿与n+2对齿交替啮合,刚度叠加,如图4-7(b)所示。由啮合刚度的定义知
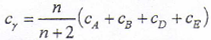
式中 cγ——啮合刚度
cA、cB、cD、cE——单对齿处于A,B,D,E啮合点处的刚度
n——重合度ε的取整值。
由于共轭齿面鼓形齿联轴器有较大的啮合重合度,其n对齿啮合时的叠加刚度与n+2对齿啮合时的叠加刚度比值较一般齿轮传动要大得多,因此它的多齿啮过渡较平稳。

对于外啮合直齿圆柱齿轮传动cγ=(cA+cB+cD+cE)/2,在单对齿刚度相同情况下,显然鼓形齿联轴器的啮合刚度要大得多。
上一页
下一页


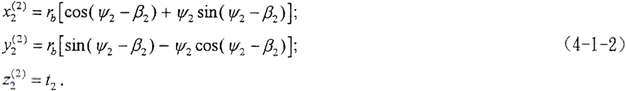

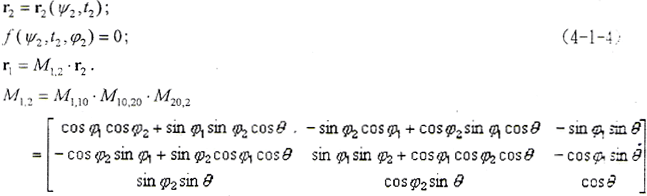

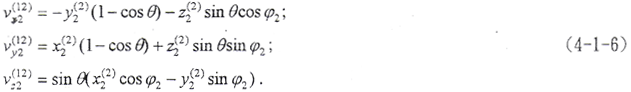
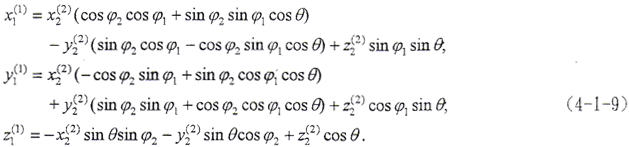
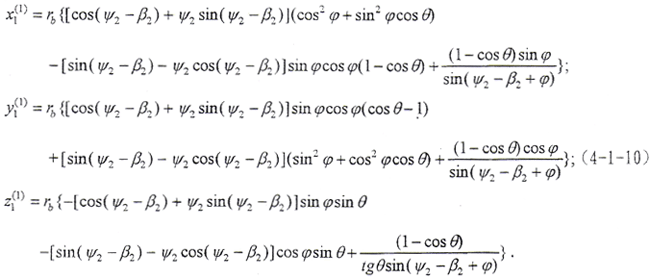
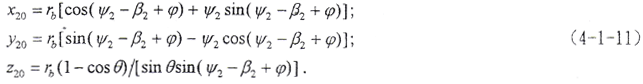
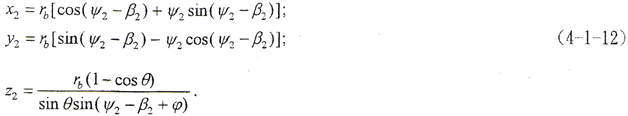


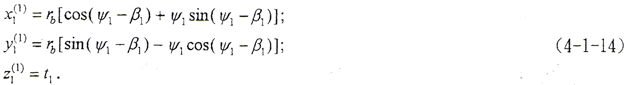
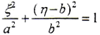
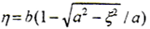 。因ξ与z1方向相同,以t1为参变量,则
。因ξ与z1方向相同,以t1为参变量,则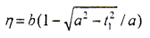
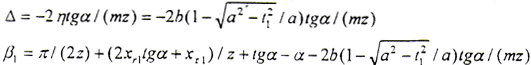
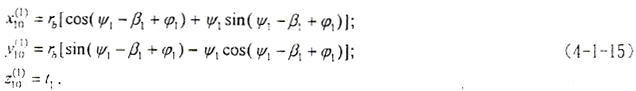
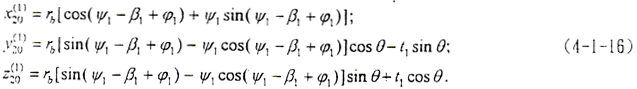
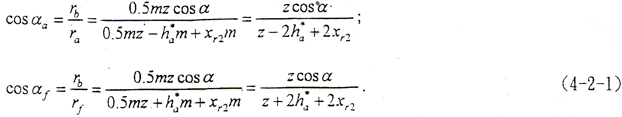


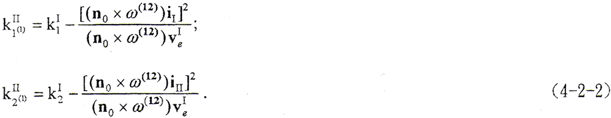

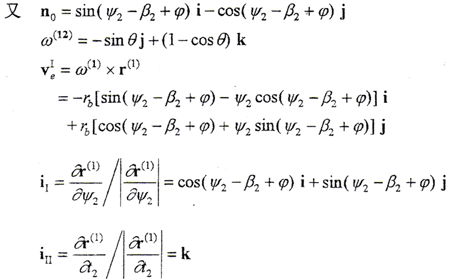
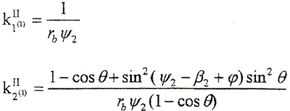
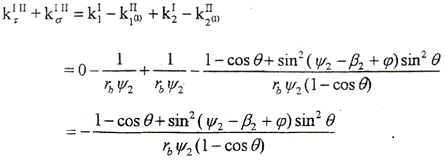
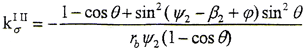
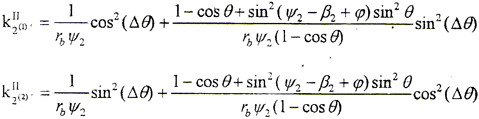
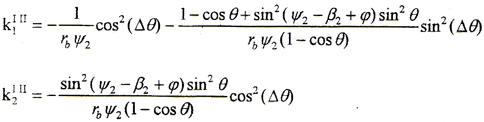

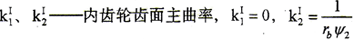
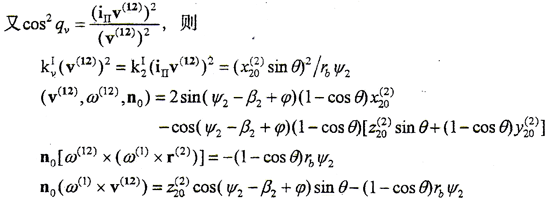
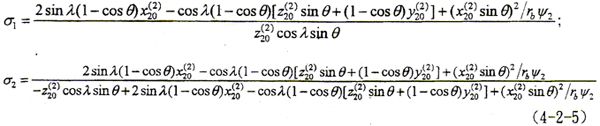

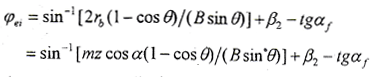

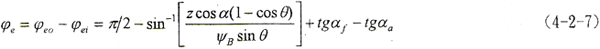
 ,所以
,所以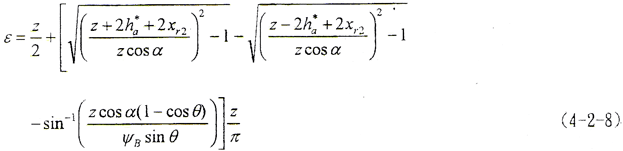



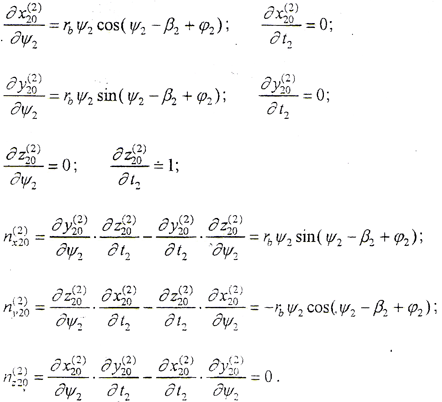
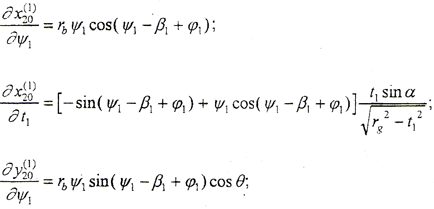
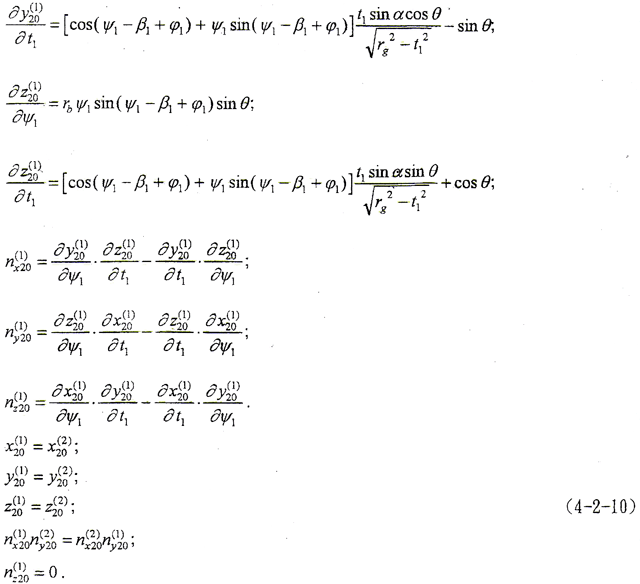
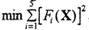 ,约束条件为tgαf1≤ψ1≤tgαa1,tgαa2≤ψ2≤tgαf2,其中αf1、αf2和αa1、αa2为鼓形外齿轮及直齿内齿轮的齿根圆压力角和齿顶圆压力角。
,约束条件为tgαf1≤ψ1≤tgαa1,tgαa2≤ψ2≤tgαf2,其中αf1、αf2和αa1、αa2为鼓形外齿轮及直齿内齿轮的齿根圆压力角和齿顶圆压力角。