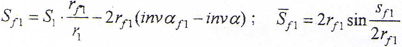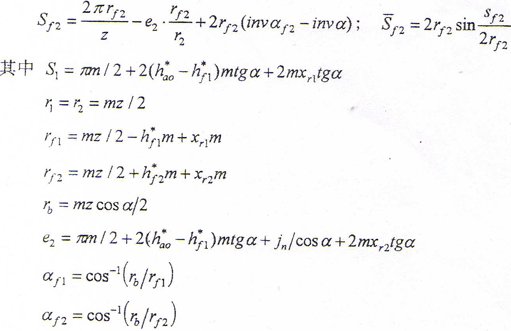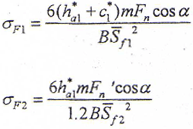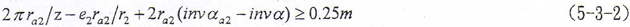第五章 鼓形齿联轴器参数优化
影响鼓形齿联轴器承载能力和工作寿命因素较多,如齿轮参数、制造质量、材料及热处理、润滑条件等等。齿轮参数的设计是其中非常重要的一个方面。由于缺乏对鼓形齿联轴器机理的研究,现在使用的齿轮参数的设计没有可靠的依据,设计计算比较粗略。通过前一章对鼓形齿联轴器的深入的啮合和力学机理研究,我们可以对齿轮参数的影响加以讨论,建立适当的参数优化模型,求解出最优的鼓形齿联轴器参数,为经济可靠地设计长寿命鼓形齿联轴器提供依据。
5.1 鼓形齿轮鼓度曲线的优化
由第四章的分析知,共轭齿面鼓形齿联轴器具有较好的传动特性,其啮合重合度大,线接触啮合,无齿面曲率干涉,等速传动等。因而接触强度高,无附加动载荷。共轭齿面鼓形齿联轴器的鼓形齿轮可采用“双分齿切齿法”加工[116],但由于该方法所用附加装置结构刚性较差,因此不适宜于加工较大模数的鼓形齿轮。非共轭齿面鼓形齿轮是在不同轴载面上采用不同变位系数形成齿面的,其变位量与轴向坐标的关系曲线就是鼓度曲线,它可以在经改装后的滚齿机上加工,加工范围不受工艺装备限制。但是根据前面分析知,传统的圆弧鼓度曲线的鼓形齿联轴器传动特性较差。因此,对鼓度曲线进行优化,使非共轭齿面鼓形齿联轴器具有更优良的传动特性,是鼓形齿联轴器参数优化的一个重要内容。
由于共轭齿面鼓形齿联轴器具有最佳的传动特性,因此将非共轭齿面与共轭齿面进行曲面逼近,所得到的非共轭齿面无疑是最佳的。
5.1.1 坐标系及坐标变换
坐标系及坐标转换关系与3.3.4.1所给相同。
5.1.2 共轭齿面鼓形齿轮齿面方程
共轭齿面鼓形齿轮齿面在S20坐标系的方程在第三章已推出为
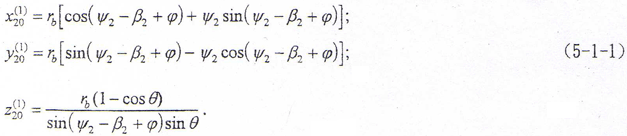
式中各量与前述相同。
5.1.3 非共轭齿面鼓形齿轮齿面方程
与第四章的非共轭齿面鼓形齿轮齿面方程推导类似,可以得出其齿面方程在S20坐标系的方程为
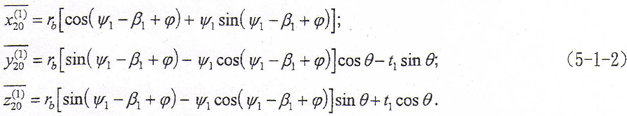
式中 β1=π/(2z)+2δtgα/(mz)+tgα-α+(2xr1tgα+xτ1)/z;δ为鼓形变位量,由不同轴截面上δ值拟合出的曲线即为鼓度曲线。其余各量与前述相同。
5.1.4 鼓形变位量δ的求解
数学方法上,两曲面的逼近是“极大极小问题”,虽已有这方面的理论探讨,但还没有成熟的计算软件。本文采用截面曲线逼近的方法(如图5-1所示),将轴向坐标离散,求得各截面上曲线逼近的δ值,再根据δ值的轴向分布形态,确定拟合的函数形式,以最小二乘法拟合出鼓度曲线。
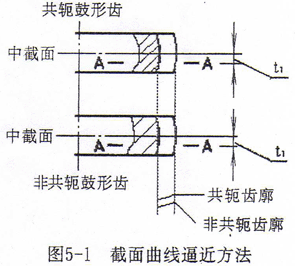
1.各截面上δ值的求解
先假设δ为零,在共轭和非共轭鼓形齿轮上截取与中截面等距离的轴截面,将两种齿面的轴截面叠合,此时,齿面与截取面的两条交线不重合;以齿面与截取面的两条交线相切为目标进行一维搜索计算,即可求得此截面上的δ值。在齿宽不同位置分别进行计算,即可求得一系列关于δ与轴向坐标的离散点坐标值。
2.鼓度曲线的拟合
通过对不同参数鼓形齿轮的曲面逼近计算,得到多组关于δ与轴向距离的离散坐标值。由离散点的分布形态及最小二乘法拟合计算知[119],拟合成双曲线的误差最小。优化鼓度曲线及其坐标如图5-2所示,拟合双曲线方程为
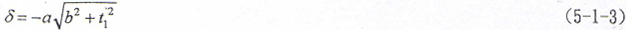
式中 a——双曲线的渐近线斜率;
b——双曲线顶点与分度圆柱线的距离。
由(5-1-1)式和(5-1-2)式,根据上述方法,可编制优化鼓度曲线参数的计算程序,用该程序,只需输入鼓形齿联轴器参数,便可计算出优化鼓度曲线的曲线参数a和b。根据多组参数计算发现,双曲线的渐近线斜率a=tgθ/tgα,与其他齿轮参数无关;双曲线顶点与分度圆柱线的距离b与各齿轮参数有关,但关系较复杂,因此该参数直接由优化计算程序得出。
文献[77]采用计算机交互图像技术进行数值分析和综合,精度受到一限制,也未给出定量解,其定性分析结果与本文的结果较接近。
5.1.5 运动分析
由第四章所给出的内齿轮齿面方程(4-1-3)式及优化鼓度曲线的鼓形外齿轮齿面方程,运用非共轭鼓形齿联轴器运动分析方法,可进行运动分析。将式(5-1-3)的δ代入(5-1-2)式的β1中,可得优化鼓度曲线鼓形齿轮齿面方程为
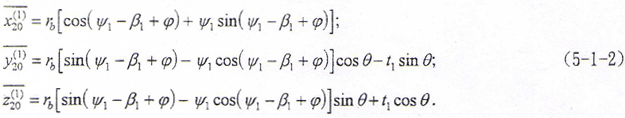
式中 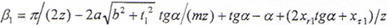
对相同齿轮参数的优化鼓度曲线和圆弧鼓度曲线鼓形齿轮联轴器在相同的轴交角下进行运动分析计算,得出的对比数据如表5-1所给。从这两组数据可以看出,在存在工作轴间倾角下,优化鼓度曲线的△φmax(°)比圆弧鼓度曲线的△φmax(°)有大幅度的减小。△φmax(°)值反映了鼓形齿联轴器运动的非匀速程度、实际啮合对数多少及啮合齿对的载荷分配情况。△φmax(°)越小,非匀速程度越小、实际啮合齿对数越多、载荷分配越均匀。因此,由啮合运动分析可以看出,优化鼓度曲线的鼓形齿联轴器比圆弧鼓度曲线鼓形齿联轴器的啮合特性有很大的改善。而且在经数控化改造后的滚齿机上,加工优化鼓度曲线的鼓形齿轮也非常方便。因此,鼓形齿轮鼓度曲线的优化是改善鼓形齿联轴器传动特性、提高其工作寿命的有效而可行的重要途径。
表5-1 啮合最大差角△φmax(°)
| 鼓形齿轮参数 |
轴交角 |
圆弧鼓度曲线 |
优化鼓度曲线 |
m=3mm z=56
位移圆半径 rg=131.0mm
双曲线参数a=0.072 b=0.060 |
1.5° |
0.090816 |
0.009631 |
| 1.0° |
0.040444 |
0.008722 |
| 0.5° |
0.010121 |
0.002179 |
m=12mm z=48
位移圆半径 rg=333.5mm
双曲线参数a=0.072 b=0.111 |
1.5° |
0.067077 |
0.019598 |
| 1.0° |
0.030581 |
0.008707 |
| 0.5° |
0.007566 |
0.002176 |
5.2 齿轮参数对鼓形齿联轴器传动特性的影响
5.2.1 模数和齿数
齿轮的模数由轮齿弯曲强度所决定。模数越大,齿根厚度越大。轮齿的弯曲强度越高。对于传递一定力矩的鼓形齿联轴器,标准中规定了其外部尺寸,即确定了齿轮的径向和轴向尺寸。由鼓形齿联轴器重合度分析知,分度圆直径一定时,减小模数、增大齿数,可以提高重合度,因此应在满足弯曲强度条件下,选用较小的模数。齿数应取为2的倍数,因为从啮合分析知,啮合的受力状态是关于原点对称的,齿数为2的倍数有利于受力的平衡。另外,对于内齿轮,还要求齿顶圆直径大于基圆直径,即
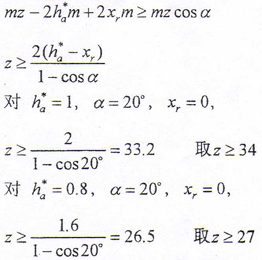
若采用正变位齿轮,其齿数可小于上述值。
5.2.2 齿高系数
齿高系数越大,重合度越大,但齿高系数的增大对重合度增大的影响较小。从齿面接触线形态看,增加齿高有利于提高接触强度。齿高增加,齿面滑动系数增加。因此总的来看不宜以增加齿顶高系数来增加重合度。
鼓形齿联轴器中,外齿轮齿顶高系数为ha1*,其齿根高系数为hf1*=ha1*+c1*;内齿轮齿顶高系数为ha2*,其齿根高系数为hf2*=ha2*+c2*,且hf2*=ha1*,在我国现行产品中有ha1*=1、hf1*=1.25、ha2*=0.8、hf2*=1和ha1*=0.8、hf1*=1.05、ha2*=0.8、hf2*=0.8两种。
5.2.3 压力角
分度圆压力角对轮齿曲率、齿根和齿顶厚度及法线方向有影响,因而也对啮合时的诱导法曲率、齿面滑动率、重合度、齿面作用力及轮齿接触应力和弯曲应力有影响。增大压力角,诱导法曲率减小、接触强度提高;齿根厚度增大,弯曲强度提高;齿面滑动率减小,改善了磨损;重合度减小,但相对减小量不大;法向力增大。考虑到市场上能方便地买到齿轮刀具,我国目前一般采用α=20°。
5.2.4 变位系数
鼓形齿联轴器是等齿数的交错轴内外齿轮传动,因此只能采用等径向变位(即xr1=xr2)。采用正的径向变位与增大压力角有类似的影响,但采用径向变位比改变压力角在加工上更容易实现,因为改变压力角需用专用的刀具。采用切向变位可以改变内外齿轮的齿厚,但不影响其他啮合特性,鼓形齿联轴器的啮合侧隙就是采用切向变位来保证的。
5.2.5 齿宽系数
齿宽系数影响轮齿的齿根弯曲强度和接触强度,齿宽系数大,两项强度值越大。齿宽系数影响重合度,在齿宽系数小于一定值范围时,其值的增大对重合度增加影响较大,而在大于这个一定值时,其值的增大对重合度增加影响较小(见图4-4b)。对于圆弧鼓度曲线的鼓形齿联轴器,齿宽还是确定鼓度半径和侧隙的参数,齿宽越大,鼓度圆弧半径越大,所需的侧隙也越大。因此,在齿根弯曲强度和齿面接触强度足够的条件下应以有较大的重合度来确定齿宽,不应盲目增加齿宽,以免使结构尺寸不必要地增加。一般取齿宽系数ψB=8~14。最小齿宽应由允许的齿根应力来确定,还要考虑由轴间倾角引起的着力点沿齿宽位移所需的宽度。
5.3 齿轮参数的优化
齿轮参数的优化是一个多目标的问题,一方面希望有最小的结构尺寸,另一方面希望有足够的强度及最佳的啮合特性。由于鼓形齿联轴器标准中已规定了外部尺寸,故本问题优化的关键是在一定的结构尺寸下确定内部齿轮参数的优化值,使其具有最佳的承载能力和最长的工作寿命。鼓形齿联轴器的失效形式,主要是外齿轮齿面磨损后轮齿折断失效,因此,增加外齿轮齿厚,提高其齿根弯曲强度和减少齿面磨损是提高鼓形齿联轴器承载能力和工作寿命的关键。
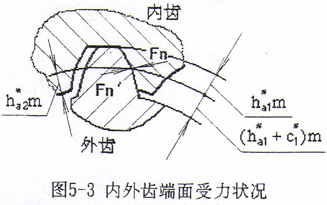
一般鼓形齿联轴器的齿顶高系数ha1*=1,径向间隙系数c1*=0.25,全齿高h=2.25m,采用标准齿轮,其内外齿轮分度圆齿厚大致相等。它的主要优点是内外齿轮加工工艺性好,可采用标准齿轮滚刀和插齿刀进行加工,且尺寸计算简单。但是这种鼓形齿联轴器的外齿轮齿根抗弯强度比内齿轮齿根抗弯强度要低,即内齿轮齿根弯曲强度有富余。因此,可设法增加外齿轮齿厚,提高外齿轮齿根弯曲强度。通常采用两种方法:一是采用特殊刀具减簿内齿轮齿厚而增加外齿轮齿厚,使内外齿轮的抗弯强度接近一致;另一种方法是采用变位短厚齿型内外齿轮,降低外齿轮齿高,加大外齿轮齿厚,使其粗短,以提高外齿轮的抗弯强度[75]。前一种方法需采用专用的瘦齿型滚刀,这给加工带来不少麻烦,因此在国内不宜推广。文献[75]所出了一种变位短厚齿型鼓形齿联轴器的设计制造方法,由于是采用标准滚刀和插齿刀进行加工,加工方法简单易行,因此工艺性好,生产效率高,是一种较理想的适宜推广应用的设计加工方法。但是,该文提出采用齿顶高系数ha1*=0.8不一定合理,因为齿顶高系数的确定一方面要使内外齿轮齿根弯曲强度一致,另一方面又要使内外齿轮齿面具有足够的接触强度及内齿轮齿顶厚应大于0.25m。因此必须建立优化数学模型进行计算来确定。将内外齿轮轮齿简化成悬臂梁受力(如图5-3所示)[127],本问题是要使内外齿轮齿根有接近的齿根弯曲强度,则目标函数为
min(σF1-σF2)2
式中 σF1——外齿轮齿根弯曲应力
σF2——内齿轮齿根弯曲应力
设齿形角α=20°,顶隙系数c1*=0.25,模数齿数为给定值,根据这种短厚齿的加工原理是减少滚刀的切入量,使其齿高系数减小,这也相当于使用齿厚减簿的滚刀来滚切鼓形外齿轮,即相当于采用了切向变位加大齿厚。其切向变位系数xτ1与齿高系数的关系为xτ1=2(hao*-hf1*)tgα,式中hao*为滚刀的齿顶高系数,通常hao*=1.25,hf1*为被切外齿轮齿根高系数,hf1*=ha1*+c1*。为了满足联轴器轴间倾角的要求,除外齿轮有一定的鼓度外,内外齿之间还应有一定的齿间侧隙jn,此侧隙可按一定的原则分配到内外齿轮齿厚上,使它们有相应的减簿量。考虑加工的因素及总的要求是减簿内齿轮齿厚、增大外齿齿厚,因此将jn全部分配在内齿轮上,则内齿轮切向变位系数
xτ2=2(hao*-hf1*)tgα+jn/cosα;jn采用以下公式计算[120]
jn=2(rg/tgα-mz/2)(1-cosθ)cosα
式中 rg——鼓度圆弧半径
对于z≥2(ha*+c*)/(1-cosα)的外齿轮齿根圆弦齿厚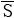 f1可近似用下式计算[121]
f1可近似用下式计算[121]
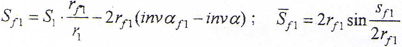
内齿轮齿根圆弦齿厚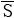 f2可近似用下式计算
f2可近似用下式计算
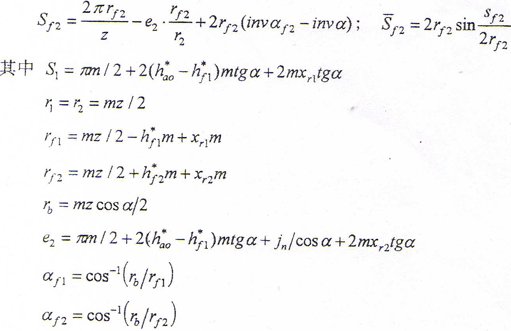
对齿式联轴器,取hf2*=ha1*、xr2=xr1。
设外齿轮齿宽为B,则内齿轮齿宽为1.2B,因此有
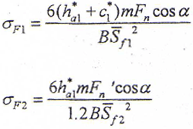
式中B、m、Fn、Fn′、α为常数,因此目标函数可写成

约束条件为Sa2≥0.25m,式中Sa2为内齿轮齿顶圆齿厚,即有
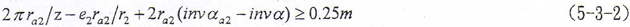
由目标函数(5-3-1)式及约束条件(5-3-2)式便构成本问题的优化数学模型。通过对优化数学模型的求解,可以计算出不同齿模数及相应的鼓度半径下的优化齿顶高系数值。表5-2给出了几种不同输入参数下的求解值,从表中数据可以看出,不同齿数及鼓度半径,其优化齿顶高系数不同,但都不超过0.7。考虑到齿顶高系数的统一,建议采用齿顶高系数为0.7是适宜的。值得指出的是,这种齿顶高系数的齿轮是采用标准齿顶高系数滚刀和插齿刀用特殊方法进行加工的。
表5-2 优化齿顶高系数值(α=20° m=3mm)
| 鼓形齿参数(θ=1.5°) |
齿顶高系数 |
鼓形齿参数(θ=2.0°) |
齿顶高系数 |
| 齿数z |
鼓度半径rg(mm) |
ha* |
齿数z |
鼓度半径rg(mm) |
ha* |
| 40 |
94.073 |
0.5874 |
40 |
70.561 |
0.5997 |
| 48 |
112.888 |
0.6247 |
48 |
84.673 |
0.6398 |
| 56 |
131.702 |
0.6555 |
56 |
98.786 |
0.6736 |
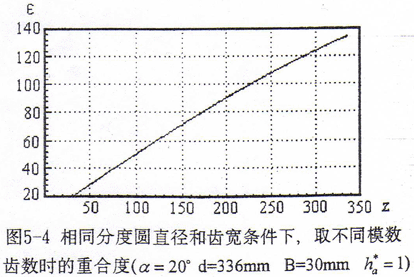
鼓形齿联轴器的齿数模数决定了其径向结构尺寸大小。对于优化鼓度曲线的鼓形齿联轴器,其啮合特性与共轭齿面鼓形齿联轴器相近,因此我们可以依据共轭齿面鼓形齿联轴器特性来考虑齿数模数的参数优化问题。图5-4给出了相同齿轮分度圆直径和齿宽条件下取不同模数齿数时的重合度曲线,从曲线可以看出相同齿轮分度圆直径和齿宽条件下,所取齿数越多,则重合度越大。重合度越大,平均每对齿承受的载荷越小,多齿啮合过渡状态载荷分配的变化量越小,传动越平稳。因此总的模数齿数的选取原则是尽可能选大的齿数。但是相同齿轮分度圆直径条件下,齿数越大,模数越小。模数的减小将降低齿根弯曲强度;另外,由齿面接触线形态知,模数的减小也将降低齿面接触强度。为保证有足够的齿根弯曲强度和齿面接触强度,应由所传递的转矩和许用应力值,先计算出所允许的最小模数,再根据这个模数值及分度圆直径来确定齿数。由于使用中磨损是不可避免的,因此,选取模数时还应考虑轮齿齿厚有一定的裕量,保证在一定的磨损程度下仍有足够的强度。另外,模数的选取还应考虑工艺条件的许可。这些内容包含较多的经验成份,在此不予详细讨论。
鼓形齿联轴器的参数优化设计是以深入的啮合特性机理分析为基础的,它必将为新型长寿命鼓形齿联轴器的设计提供重要的理论依据。
上一页
下一页

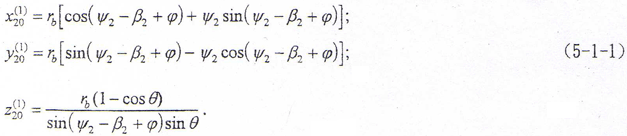
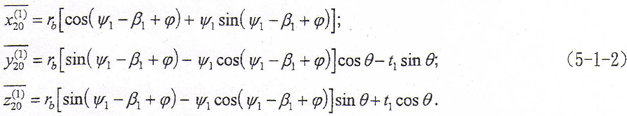

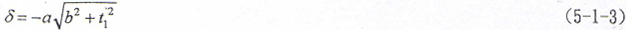

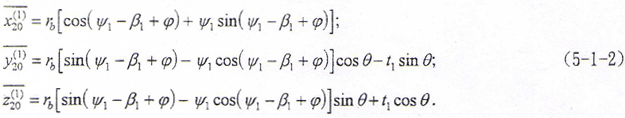
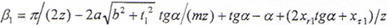
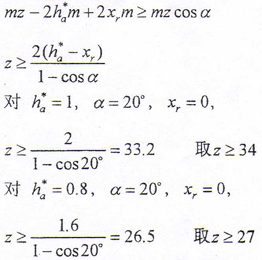

 f1可近似用下式计算[121]
f1可近似用下式计算[121]