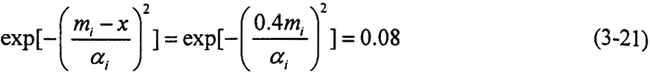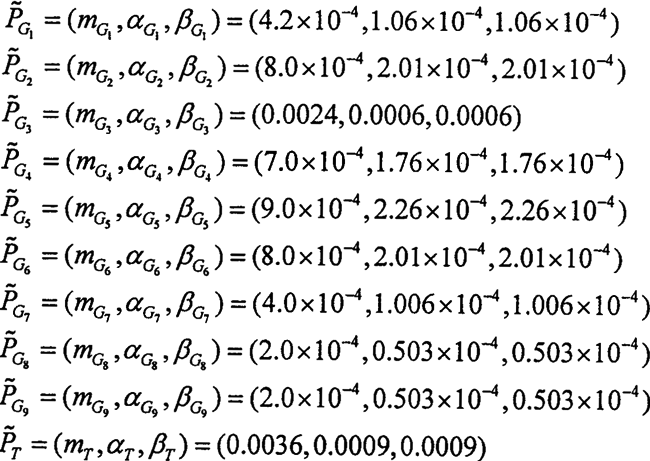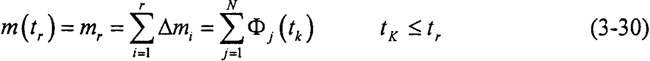故障树中各事件发生的概率用模糊数来表示,根据模糊数的运算法则式(3-13)、(3-15)和模糊算子AND和OR的计算方法式(3-18)、(3-20)即可确定顶事件发生的模糊概率。假定事件发生概率Pi的参照函数为正态对称型,其隶属函数如式(3-11)所示,且与均值mi相差±40%的点x的隶属度为0.08,则
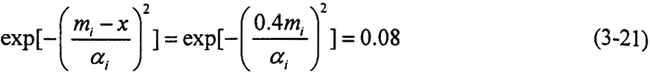
故αi=βi=0.2517mi,各底事件的故障概率均值mi及左右分布αi、βi如表3-4所示。
表3-4 底事件的故障概率均值mi及左右分布αi、βi
| 代号 |
底事件 |
均值mi |
分布αi和βi |
代号 |
底事件 |
均值mi |
分布αi和βi |
| X1 |
电源未开 |
2×10-5 |
5.034×10-6 |
X9 |
导架接触失效 |
3×10-4 |
7.551×10-5 |
| X2 |
电源开关失效 |
1×10-4 |
2.517×10-5 |
X10 |
活齿接触失效 |
2×10-4 |
5.034×10-5 |
| X3 |
系统保险丝烧断 |
3×10-4 |
7.551×10-5 |
X11 |
壳体接触失效 |
2×10-4 |
2.517×10-5 |
| X4 |
轴Ⅰ断裂 |
3×10-4 |
7.551×10-5 |
X12 |
轴承1失效 |
1×10-4 |
2.517×10-5 |
| X5 |
轴Ⅱ断裂 |
5×10-4 |
1.258×10-4 |
X13 |
轴承2失效 |
1×10-4 |
2.517×10-5 |
| X6 |
活齿接触失效 |
2×10-4 |
5.034×10-5 |
X14 |
轴承3失效 |
1×10-4 |
2.517×10-5 |
| X7 |
主动轴接触失效 |
1×10-4 |
2.517×10-5 |
X15 |
轴承4失效 |
1×10-4 |
2.517×10-5 |
| X8 |
活齿拦触失效 |
2×10-4 |
5.034×10-5 |
|
|
|
|
据式(3-20)及表3-3中所列的真值函数形式,计算可得各中间事件及顶事件发生概率的模糊数为:
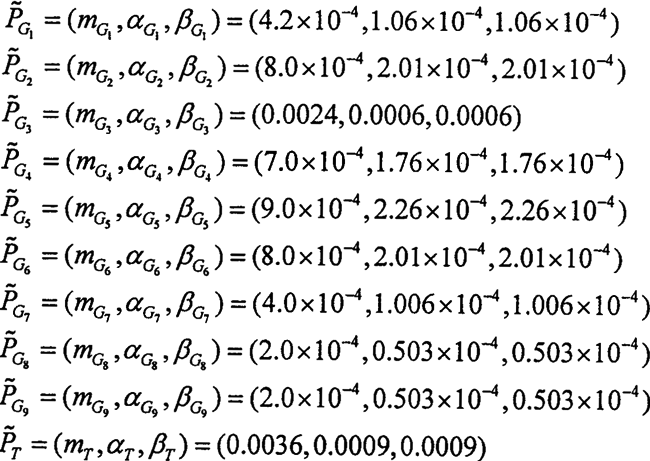
从中间事件发生概率的模糊数看,中间事件G3发生的概率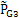 比其他中间事件发生的概率都要高,也就是说活齿运动副失效是造成顶事件发生的主要因素,而在导致G3发生的各中间事件里,事悠扬G5发生的概率
比其他中间事件发生的概率都要高,也就是说活齿运动副失效是造成顶事件发生的主要因素,而在导致G3发生的各中间事件里,事悠扬G5发生的概率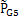 最大,即活齿与导架的运动副失效是导致活齿运动副失效的关键,因此为降低顶事件发生概率,提高整个系统可靠性,应尽量提高导架与活齿啮合副的接触强度的可靠性。顶事件发生概率弃
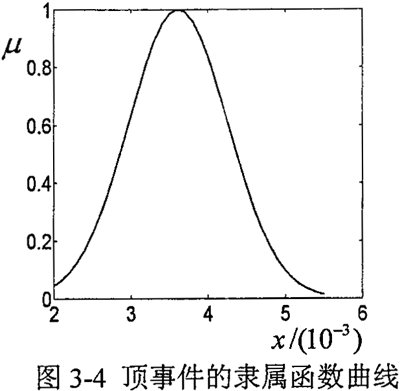
最大,即活齿与导架的运动副失效是导致活齿运动副失效的关键,因此为降低顶事件发生概率,提高整个系统可靠性,应尽量提高导架与活齿啮合副的接触强度的可靠性。顶事件发生概率弃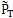 的隶属函数曲线如图3-4所示。它表示与圆柱正弦活齿减速器输出轴不能传递扭矩故障概率均值0.0036相差士40%的点的隶属函数为0.08,分布α=β=0.0009。可见此系统的顶事件模糊概率的均值和左右分布都很低,所以该系统是安全的。
的隶属函数曲线如图3-4所示。它表示与圆柱正弦活齿减速器输出轴不能传递扭矩故障概率均值0.0036相差士40%的点的隶属函数为0.08,分布α=β=0.0009。可见此系统的顶事件模糊概率的均值和左右分布都很低,所以该系统是安全的。
3.4基于Monte-Carfo方法的减速器系统可靠性数字仿真
在某些复杂系统可靠性分析中,采用传统的人工评定方法很难完全解决系统可靠性的有关问题,数字仿真为解决这类问题,提供的一条新的有效途径。通过仿真不仅可以求解系统可靠性的点估计值,还可以得到统计值的分布函数,这对深入了解系统具有很大的帮助。此外,借助仿真运行的过程还可以系统内各部分可靠性所产生的作用,获得系统内部可靠性更多的信息,这对改进系统和重新设计系统具有很大的指导意义。
3.4.1减速器系统仿真模型的建立
采用Monte Carlo法对减速器系统进行可靠性数字仿真,系统U可表示为
U={Z1,Z2,…,Z15} (3-22)
式中Zi——系统第i个基本部件。每个基本部件的失效分布函数为Fi(t), (i=1,2,…15)。
由故障树表达的逻辑关系可以看出顶事件即为系统的失效事件,底事件即为基本部件的失效事件。设故障树的结构函数为Y,Y包括与门和或门。顶事件在t时刻的状态变量用Φ(t)表示,则

且Φ(t)的取值为
Φ(t)=Y[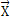 (t)] (3-24)
(t)] (3-24)
式中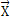 (t)——第i个底事件的状态变量。
(t)——第i个底事件的状态变量。
且有

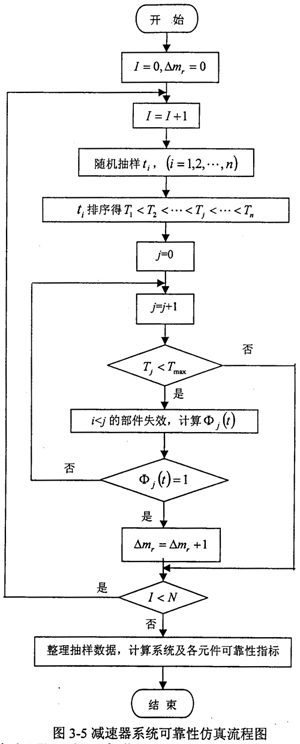
3.4.2减速器系统可靠性仿真流程
用Monte Carlo法对圆柱正弦活齿减速器各基本部件寿命进行随机抽样,以获得每个基本部件故障时间的简单样本。在第j次抽样的,第i个基本部件失效时间抽样值为
tij=Fi-1(ηij) (3-26)
式中ηij——第i个基本部件在第j次抽样的的随机数。
根据式(3-25)和式(3-26),可知在第j次抽样中第i个底事件在t时刻的状态变量为

在第j次抽样中,若系统失效时刻时tkj,利用故障树的结构函数可知顶事件在t时刻的状态变量为

第j次抽样,可产生15个基本部件的失效时间tij(i=1,2,…,15),将失效时间按照由小到大的顺序排列为t?1,t?2,…,t?15,与之对应的基本部件顺序表示为Z1′,Z2′,…,Zk′,…,Z15′。首先将基本部件Z1′设为失效,即t=t?1,而其它部件均未失效,检查此时系统U是否失效,即Φj(t?1)是否为1。若减速器系统未失效,则将基本部件Z2′设为失效,检查系统U此时是否失效…,直到基本部件Zk′失效,即t=t?k时,此时Zk′之前的基本部件均已失效,如果系统处于失效状态,即Φj(t?k)=1,则第j次抽样时系统寿命抽样值为tkj<,其值为t>kj=t?k。至此,第j次抽样结束。依此类推可得到各次抽样的系统寿命抽样值。经过N次抽样后,对其作统计处理,统计N次抽样各底事件发生引起顶事件发生的频率,根据大数定理,当抽样次数足够多时,事件发生的频率将趋近事件发生的概率,进而可以计算系统的可靠性指标。本文取抽样次数为5000次,并分析其误差范围。可靠性仿真的流程图见图3-5。
采用区间统计法,首先设减速器最大工作时间为Tmax,将它分为m个相等区间,则第r个区间记为[tr-1、tr],r=1,2,…,m。设系统仿真的总次数为N,若第j次抽样减速器失效的时间为tk,判断落入哪个工作区间[tr-1,tr]内,并利用Φj(tk)统计出N次仿真后,减速器失效时间的分布,即

式中 △mr——系统在[tr-1,tr]区间内的失效次数。
t≤tr的减速器失效数为
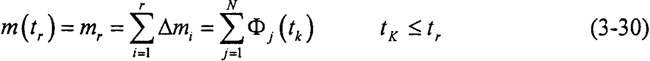
在通扫故障树足够多次九的基础上,通过对获得的数据进行分析,即可得到圆柱正弦活齿减速及各组成部分的各项可靠性指标。计算方法如下:
系统可靠度为:


式中 nsi——基本部件Zi失效引起系统失效的次数;
ns——系统失效总次数。
基本部件的模式重要度表示系统可靠性的薄弱环节,WN(Zi)最大的元件就是系统最薄弱的环节。
3.4.3减速器系统可靠性数字仿真分析结果
根据故障树对圆柱正弦活齿减速器进行可靠性的数字仿真研究。各基本部件寿命分布参数见表3-5,采用上述算法编程求解。通扫故障树5000次,产生减速器寿命抽样值5000个,设系统最大工作时间Tmax为1000Oh,将Tmax分为1000个区间,统计减速器寿命抽样落入各区间的次数,得到系统平均寿命,即减速器平均无故障工作时间MTBF为3086h,寿命的方差为6.39×106。根据仿真结果进行拟合分析,系统寿命服从威布尔分布,即

式中 ηs=3.26×104;βs=1.1605。
仿真的系统可靠度曲线Rs、拟合的可靠度曲线R0,及R0的置信上、下限曲线RU、RL如图3-6所示。减速器可靠性仿真的误差分析及基本元件的模式重要度如表3-6和表3-7所示。
表3-5 基本元件失效分布类型及参数
从图3-6可以看出,拟合的可靠度R0与仿真的可靠度Rs十分接近,均介于置信度为95%时的置信上、下限RU、RL之间,并且仿真误差很小。因此,系统可靠度仿真方法是有效的。当仿真次数增大时,仿真结果将更令人满意。

表3-6 减速器可靠性仿真误差分析
| tr(h) |
不可靠度估值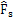 (tr) (tr) |
可靠度RS(tr) |
仿真的误差估计ε |
| 100 |
0.0056 |
0.9944 |
<0.0021 |
| 500 |
0.424 |
0.9576 |
<0.0056 |
| 1000 |
0.960 |
0.9040 |
<0.0082 |
| 3000 |
0.3010 |
0.6990 |
<0.0127 |
| 8000 |
0.6350 |
0.3650 |
<0.0133 |
从表3-7模式重要度WN(Zi)可以看出,导架的模式重要度WN(Z9)远远大于其他部件的模式重要度,表明导架是系统薄弱环节,其可靠性对减速器的寿命影响最大,导架的失效模式主要是疲劳点蚀及磨损失效等,所以提高导架的接触强度的可靠性是改善圆柱正弦活齿减速器可靠性的关键。
表3-7 基本元件模式重要度
| 部件代号 |
WN(Zi) |
部件代号 |
WN(Zi) |
部件代号 |
WN(Zi) |
| 1 |
0.0378 |
6 |
0.0678 |
11 |
0.1076 |
| 2 |
0 |
7 |
0.1026 |
12 |
0.0788 |
| 3 |
0 |
8 |
0.0690 |
13 |
0.0804 |
| 4 |
0.0134 |
9 |
0.2006 |
14 |
0.0778 |
| 5 |
0.0174 |
10 |
0.0730 |
15 |
0.0738 |
3.5本章小结
1.对圆柱正弦活齿传动进行了接触强度的模糊可靠性分析。基于模糊数学方法和可靠性设计理论,将应力和强度分别视为随机变量和模糊变量,建立了零件接触强度的模糊可靠性数学模型和计算公式;
2.在分析圆柱正弦活齿减速器组成结构及各种失效可能的基础上,建立了以“输出轴不能传递扭矩”为顶事件的减速器故障树。通过定性分析,找出了减速器的全部最小割集,即导致顶事件发生的所有可能方式。给出了减速器中间事件和顶事件的真值函数计算公式;
3.将模糊数学引入圆柱正弦活齿减速器的故障树分折中。采用参照函数为正态型的L-R模糊数描述各底事件的发生概率,根据模糊数的运算法则和模糊算子AND和OR的计算方法,推导出圆柱正弦活齿传动系统输出轴不传递扭矩顶事件发生的模糊概率及其隶属函数分布;
4.为模拟真实工况下减速器的可靠性情况,在建立的故障树基础上,采用Mollte-Carlo方法随机生成基本事件的故障概率,对减速器进行可靠性数字仿真。通过分析仿真结果,得到减速器系统的寿命分布及各零件模式重要度,为分析、改进系统指明了方向。
上一页
下一页