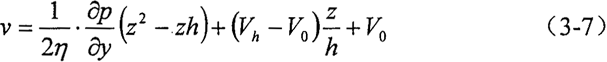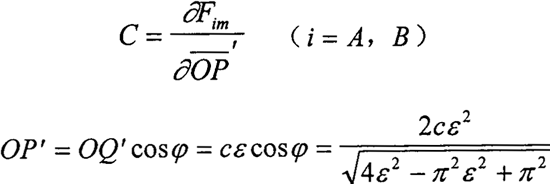第3 章 偏心转动及动载荷工况三环减速器油膜浮动均载的研究
3.1 引言
由于三环减速器充分地利用了功率分流和内啮合多齿接触的原理，因此，三环减速器的承载能力较大。上一章的受力分析和振动分析表明：采用三片内齿环板偏心之间呈180°相位角的布置形式，能够实现惯性力和惯性力矩的完全平衡，又使得啮合力对振动的影响减小，采用双轴输入又可使三环减速器各环板所受的啮合力相等，避免机构的过死点的冲击，改善高速轴的受力情况，提高传动系统的效率。在双轴输入和完全平衡状态下，啮合力对输出轴支撑轴承的作用力和作用力矩也完全平衡。由于不可避免的制造和安装误差及动力传递过程中出现的零部件变形，使得三片内齿环板之间的作用载荷分配不均匀，引起动载荷增加，导致振动加剧，造成齿面点蚀、轴承损坏、齿轮箱发热，甚至发生事故。本文提出的同步带传动作为一级传动的完全平衡均载减振的三环减速器，可实现减速器齿轮传动部分的惯性力和惯性力矩完全平衡和三环传动的双轴输入，克服了死点位置冲击和振动较大的问题。该减速器的油膜浮动实现了三苏减速器均载和减振。由于本文提出的油膜浮动方案是在旋转的偏心轴表面与转臂轴承之间插入一个圆柱套筒形成的，并受到一个动载荷的作用，其动力学研究尚未见到相关的报道，本章对油膜浮动动力学的有关问题进行研究。
3.2 两级三环减速器的误差分析
由于不可避免的制造和安装误差的影响，三片传动环板所承担的载荷并不相同，这种现象严重影响着三环传动优越性的发挥，使得轮齿在啮合时产生振动，发出噪音，严重时会导致异常工作情况甚至出现事故。减少或消除制造和安装晨差引起的各行星轮载荷分配不均的问题影响的有效方法是在结构设计中采用均载机构，通过均载机构的弹性变形使得三环传动过程中的各构件之间能够自动补偿误差，从而达到各传动环板受载均匀的目的。
三环减速器制造安装误差中影响载荷分配的主要因素是：偏心套偏心误差Em、环板内齿轮偏心误差Er及输出外齿轮偏心误差EW,由于轴承、传动轴以及齿轮的齿形、基节等的制造误差相对于前面的几项偏心误差很小，故可忽略不计。
选择不同的均载构件，其等效中心误差是不同的，本章选择如图3-1所示的在三环减速机的转臂偏心轴套与转臂轴承之间插入一转动套筒，在偏心轴和套筒之间以及套筒与轴承内表面之间形成动压油膜的油膜浮动均载方案。
为此应将三环减速机的单个构件的误差即：偏心套偏心误差Em、环板内齿轮偏心误差Er及输出外齿轮偏心误差Ew等效换算到均载构件偏心轴上以得到等效中心误差。下面简要分析各种制造安装误差的影响：
构件误差使环板转臂轴承的中心相对其理论位置产生的位移可分解为环板内齿轮的啮合力反力方向位移和啮合力反力垂直方向位移，前者需要均载机构来补偿，后者仅相当于使内齿轮绕其瞬心做了一个微小转动，只会导致啮合轮齿间的齿面滑动，不会改变内齿环板的受力，因此，转臂偏心轴的浮动量为构件误差所要求的转臂轴承中心位移在啮合力反力方向上的分量（有效位移）。由文献的误差分析知：
偏心套偏心误差与等效中心误差的关系：Em′=Em
环板内齿轮偏心误差与等效中心误差的关系：Er′=Er
外齿轮与等效中心误差的关系：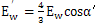
式中α′——啮合角。
为此，以偏心轴为均载构件，在最不利情况下均载构件的最大位移量为各等效中心误差的累计值：
实际上，影响总等效中心误差的因素很多，例如构件温度变形、弹性变形和轴承间隙等等。各等效中心误差都为时间的周期函数，且其相位为等概率密度。故在任一时刻，它们不可能是同向的。因此，按平方和的方法计算均载构件的位移量更为合适，即：
根据实验样机DQSH145的参数及误差分析得：
偏心套偏心误差为Em=0.030mm；
内齿轮偏心误差为Er=0.060mm；
外齿轮偏心误差为Ew=0.060mm；
这里：内齿轮和外齿轮的偏心误差近似取其相应径向跳动公差的一半。
所以，制造安装误差等效到偏心轴的径向位移的最大值Emax=0.092mm；也就是说，所有零件在载荷作用下产生的变形与偏心轴上的油膜浮动的受力变形之和，应该能使偏心轴中心产生0.O92mm的径向位移量。
3.3 动力润滑的基本方程-Reynolds方程
Reynolds方程是流体润滑理论最基本的方程，它是根据流体力学的连续方程和运动方程推导的。
连续方程
式中u,v,w——分别为沿坐标x, y,z方向的流速；X,Y,Z——体积力分量；p——密度；η——粘度；t——时间。
几点假设
（1）忽略体积力的作用，如重力或磁力等。除磁流体润滑( Magnetohydrodynamic Lubrication,MHD）外，这一假设通常是正确的。即：X=Y=Z=0
（2）流体在界面上无滑动，即贴于界面的油层速度与界面速度相同。这已被实验证实。
（3）在沿润滑膜厚度方向上,不计压力的变化。由于膜厚仅百分之几毫米,事实上压力不可能发生明显的变化。
（4）与油膜厚度相比较，轴承表面的曲率半径很大，因而忽略油膜曲率的影响，并用平移速度代替转动速度。
（5）润滑剂是牛顿流体，这对于一般工况条件下使用的矿物油而言是合理的。
（6）流动为层流，油膜中不存在涡流和湍流。对于高速大型轴承，可能处于湍流润滑。
（7）与粘性力比较，可忽略惯性力的影响，包括流体加速的力和油膜弯曲的离心力。然而，对于高速大型轴承需考虑惯性力的影响。即：
du/dt=dv/dt=dw/dt=0
（8）沿润滑油膜厚度方向粘度数值不变。这个假设没有实际根据，只是为了数学运算方便所作的简化。
（9）速度梯度中，
比较大，其他速度梯度都很小，只保留，其它删除。
在以上假设的基础上，Navier-Stokes方程可简化成：
将式（3-4）对z积分两次，于是
用边界条件确定C1和C2。由于界面上流体速度等于界面速度，如果两固体表面的速度为U0和Uh，即当z=0时，u=U0；当z=h，u=Uh。求得
因此，润滑膜中任意点沿X方向的流速为
同理对式（3-5）积分求解可得：
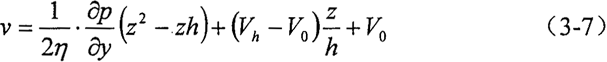
润滑油膜是在不破裂的情况下工作的，所以必须满足连续方程（3-3）。
将（3-6）和（3-7）式代入（3-3）式得：
由0到h对y求积分得
利用含参变量的定积分公式积分等式右边，并令U=U0+Uh，V=V0+Vh，则得
此式就是普遍形式的Reynolds方程。
必须强调指出：上式的Reynolds方程是根据一系列假设推导出来的，适用于一般工况条件的润滑计算。在特殊的工况条件下，当某些假设不能成立时，必须针对具体情况推导相应的Reynolds方程形式。
3.4 油膜浮动均载机理及用于三环减速器的研究
日本高桥崇发明的在行星轮中间放置浮动中间轮的油膜浮动装置独具匠心，它以结构简单、均载效果好而著称于世。该均载方式是基于滑动轴承理论，在行星轮与行星轮轴承之间装设一中间环，该环与行星轮孔之间留有径向间隙并储有润滑油，运转时，形成动压油膜。当行星轮间载荷分配不均匀时，径向力变化将引起油膜厚度变化，进而引起偏位角改变，即各行星轮对行星轮轴承产生不等量的位移，从而实现均载。理论分析和应用实践证明：油膜浮动均载效果好、结构简单、轴向尺寸小、造价低、减振性能好。三环减速器的优越性也完全依赖于“功率分流”，各环板之间实现载荷均衡就成为一个十分重要的问题。
完全平衡均载的两级三环减速器的油膜浮动装置就是一个滑动轴承。就是在三环减速器输入轴偏心套与环板转臂轴承内圈之间插入一个能够自由运动的浮动套筒（浮环），偏心轴旋转时，在油膜力的作用下浮环随之旋转，转臂轴承内圈又随浮环旋转。这种结构减小了偏心套与轴承内圈、偏心套与输入轴的刚性接触，提高了偏心套及环板轴承的寿命。上一章已对双驱动工况（由同步带实现）传动环板转臂轴承A及B处的反力进行了研究，并给出了计算公式。由环板转臂轴承处的反力分力公式知，轮齿在啮合过程中，啮合力增大时，环板转臂轴承处的反力的各分力也增大，A、B点合力也增加。
先按普通滑动轴承的情况进行分析。由于环板转臂轴承属径向短圆柱滚子轴承，根据半Aommerfeld条件，沿连心线方向和沿连心线垂直方向的总分力分别为：
式中 W——总载荷；c——半径间隙；U——轴表面圆周速度；ε——偏心率；η——粘度；L——轴承的总轴向长度。
由（3-14）式知，外载荷W增加，则偏心率ε也相应增大。
下面是偏位角公式：
由上式知：当ε增大时，偏位角的余弦增加，偏位角φ减少，偏位角φ的减少降低了接触面的温升，更重要的是浮环内表面与偏心套外表面、浮环外表面与浮环轴承内表面均形在了油膜，这对三环减速器有良好的均载效果。
当某一环板上的啮合力Fn增加时，环板转臂轴承所受的合力：
随之增加，该力需与环板上两油膜力对应相等。
相应轴承单位面积载荷为：
式中n——轴的转速。
轴承单位面积载荷也随之增加，ε也增大，偏位角φ变小，最小油膜位置点将沿着近似以c为直径的半圆周轨迹由Q′移到Q″点。也就是环板转臂轴承中心的位置将同时移动，由于移动的大小和方向不完全相同，则环板相对于水平线有微小转动，平动和转动的结果使环板中心的位置将沿轮齿啮合方向移动P′P″，即啮合处得到放松P′P″，该环板轮齿上的载荷自然会减少，按同样分析方法，同时啮合的另一环板，使内啮合变紧，啮合力增加，从而达到各环板载荷均衡的目的。
据滑动轴承理论，油膜刚度系数C为：
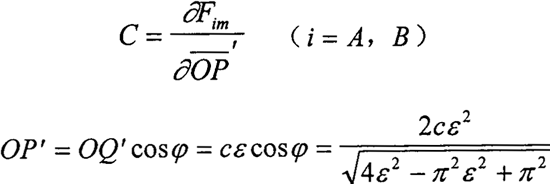
由于OP′和FAm、FBm均是ε的函数，（FAm、FBm取之一，以Fim表示，ε角标暂不考虑）
上式是按滑动轴承理论进行的，与我们设计的油膜浮动装置有重要区别。我们设计的油膜浮动均载方案，共有两层油膜，即：偏心套与浮环、浮环与滚动轴承之间各形成一层共转滑动轴承油膜，设浮环内外半径为r、r′，c、c′为浮环的内外半径间隙，C1为环板的浮动量，由摩擦学理论可导出共转轴承的浮动量C′和半径间隙c′与普通滑动轴承的浮动量C和半径间隙c之间的关系下：
也就是说，当环板各轴承所受的载荷变化时，将时环板轴承孔中心产生较大的位移，使环板内齿轮与输出轴上外齿轮啮合处产生一定的位移的松脱或巾紧，以达到各环板均载的目的。刚度越小，说明浮动装置对载荷变化的敏感程度高。
而载荷分配不均匀系数与传动系统的刚度成正比关系，对于新型三环减速器的高速轴支撑，其刚度为：
，而动力传动对轴和轴承的刚度和强度有较高的要求，因而，只能降低油膜的刚度。采用上述环板结构，相当于两弹簧串联，其刚度降氏，使各环板承受的载荷大小趋于均匀。
3.5 偏心转动及动载荷工况三环减速器油膜浮动的数学模型
以普通形式的Reynolds方程为基础，下面建立偏心转动工况下三环减速器油膜浮动时的动和方程的具体表达式。
实际上，实用的机器难以想象在某种运动系统中两个相互垂直方向上都有油楔和速度。因而，通常可把轴线安排成使：
这时，Reynolds方程可写成：
上一页
下一页
