油膜浮动均载机构的几何关系如图3-2和图3-3所示

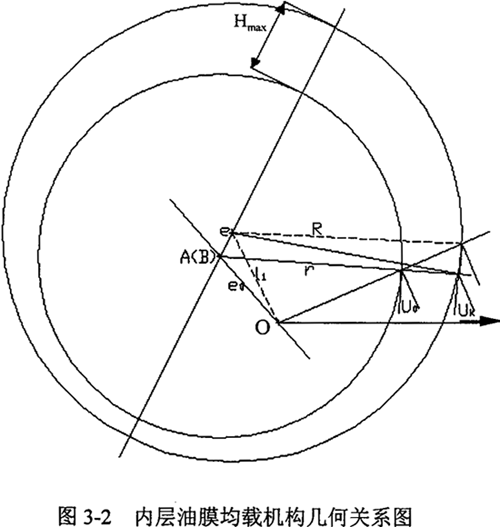
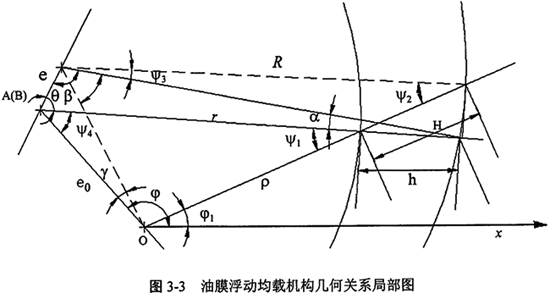
下面以图3-2和图3-3所示的内层油膜浮动为例进行推导。

h=C(1+εcosθ)

这里，U=ωr。

尽管这种简化处理与实际不完全相符，但这样做有两个好处：一是如不进行简化，就会带来极大的复杂化；二是使设计更为安全。

3.6方程的求解

对于普遍形式的Reynolds方程，仅具有特殊间隙形状的问题才能求得解析解。而对于复杂的几何形状或工况条件下的润滑问题，根本无法用解析方法，求解，电算技术使得数值解法成为润滑问题求解的有效途径。本文应用对于线性椭圆型问题最优化的数值方法一多重网格方法求解Reynolds方程。

3.6.1多重网格方法

多重网格方法的思想早在30年代就有人提出，但真正广泛应用于工程技术问题是在1977年Brandt教授发表他的开创性文章“边值问题多重网格适应解之后才开始的。由于多重网格方法求解细网格层上离散方程的总计算量与最细网格层节点数成正比，即W=O（N_l），这一指标从根本上克服了经典迭代法解离散方程的工作量一般为W=O（N_l²～W=O(N_l³)这个缺点，且多重网格方法的敛速与h无关这一特性又从根本上克服了经典迭代法的敛速与h有关，越细所需迭代步越多，Ω_l越细所需迭代步越多，敛速越慢这个缺点。如今，多重网格方法已被广泛应用于各门学科和各种工程技术问题中，并取得了许多研究成果。文献将多重网格方法用于求解动载荷滑动轴承的润滑问题，并取得了成功。用多重网格方法求解润滑方程，在满足精度的条件下，较Gauss-Seidel等经典方法收敛速度快，节省计算机时间，而且求解可靠，是一种很有应用前景的求解大型代数方程组的数值迭代法。

考虑线性二阶椭圆边值问题（以两层网格为例说明）

Lu=f           （Ω）                     （3-30）

Ω是一个给定的连续域，L是Ω上的线性椭圆微分算子矩阵，u为要求方程Lu=f的解，右端项f为已知的量。用上标h和H别表示细网格和粗网格，将上式在连续域Ω上离散，其在细网格和粗网格离散的差分方程分别为

L^hu^h=f^h         （Ω_h）                            （3-31）

设差分方程的粗确解为u^h，差分方程的迭代解为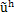，以?^h为初值，在细网格上对L^hu^h=f^h做v₁次迭代，得近似值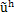和残差r^h

r^h=f^h-L^h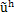                                     （3-33）

定义：

r^h=L^hv^h                                     （3-34）

有：

?f^h=L^h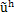+L^hv^h                                   （3-35）

这样：

u^h=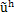+v^h                                      （3-36）

修正项v^h不是在细网格上计算的，而是在粗网格上根据下式求得的。

L^Hv^H=I_h^Hr^h                                      （3-37）

这里，I_h^H是从细网格到粗网格的限制算子，一般选用全权限制算子。

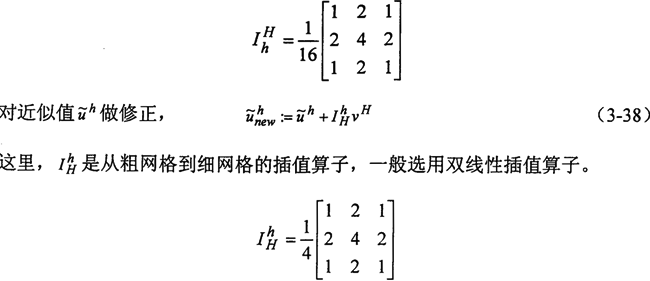
上述过程重复进行，直至在最粗网格上得到满足精度要求的精确解。

图3-4所示为三层网格上的一个循环的具体计算步骤。

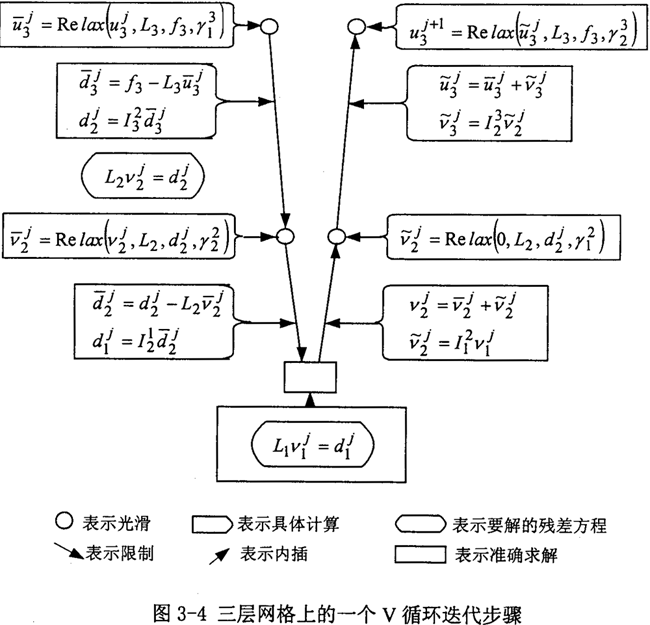
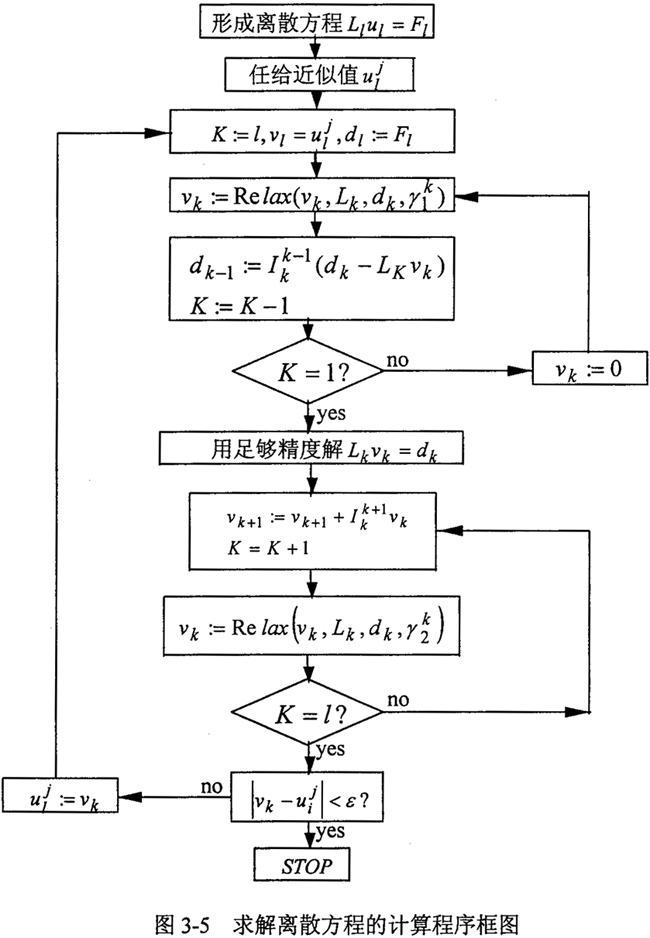
图3-5所示为l个网格层上利用V循环求解离散方程（3-31）式计算框图。

3.6.2 差分方程

由于将有量纲方程化为无是纲形式后，方程形式主得简单，便于计算，而获得的结果又便于推广到与此轴承相似的各类尺寸的轴承，故，有必要将雷诺方程无量纲化。

为了求解雷诺方程，将油膜压力区展成一矩形域，用无量纲形式的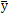和油膜角θ分别表示矩形域的宽和长。并将该求解区域离散成若干个相等的矩形网格。考虑到油膜压力在轴的宽度方向对称分布，即：方程的解关于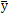=0对称，因而，油膜压力区只需计算一半即可。

在［0,l］区间n等份，在［0,2π］区间m等份，即可构造出方程（3-40）的（i，j）离散差分方程：

L_k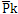=f_k                               (3-41)

其边界条件为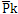：    (i,n)=0,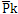(i+m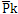,j)=(i,j)

该方程满足多重网格方法的条件，可用多重网格方法求解。

3.6.3 油膜承载能力的计算

若液体压力以解析表达式给出，油膜浮动的承载能力可由3-10和3-11式直接积分求得。但由于本节方法求出的压力是离散值，其承载能力需用数值积分求解。本文通过采用Simpson 积分公式的方法，分别沿周向和轴向迭加求值。

沿周向的一般情形的复合Simpson积分公式为：

3.6.4 计算结果的讨论

根据上面的计算公式，笔者编写了油膜压力分布和油膜浮动时的承载能力FORTRAN计算程序。计算中所采用的是V循环，网格层数为6，最粗网格数为：12×2，最细网格数为：64×384。计算的部分结果如图3-6和图3-7所示。

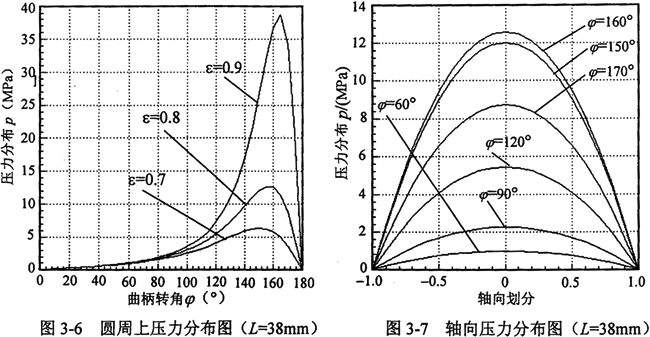
由图3-6可看出，相同浮动套长度时，圆周上的压力随着偏心率的增大而增大，且在压力最大值时的变化幅度较大。另外，计算还证明：在偏心率相同的条件下，圆周上的压力随着浮动套长度增大而增大。

由图3-7可看出，油膜浮动时的压力沿轴向近似成抛物线形状，但在不同的角度下其值则是不同的。

表3-1 不同的工况下轴膜浮动的承载能力

偏心率	ε1=0.7	ε2=0.8	ε3=0.9
油膜承载力P（N）	3768	8236	34486

笔者的结果表明，在偏心套长度确定的条件下，油膜浮动时油膜的承载力主要取决于偏心率，笔者设计的油膜浮动均载装置便是以此为基础。

3.7 本章小结

本章在对两级三环减速器的主要制造安装误差进行系统分析的基础上，依据流体动力润滑理论研究了两级三环减速器油膜浮动均载机理，建立了偏心转动和动载荷工况下两级三环减速器油膜浮动时的流体动力润滑方程，采用多重网格方法和Simpson 积分公式对样机油膜浮动的承载能力进行了计算。均载的目的就是要减少或消除制造安装误差的影响，为此，本章首先对两级三环减速器的主要制造误差进行了系统分析，计算了需补偿的位移量。依据流体动力润滑理论对两级三环减速器应用油膜浮动的可行性和三环减速器油膜浮动的均载机理进行了研究，结果表明：两级三环减速器应用油膜浮动进行均载是切实可行的。

依据流体动力润滑理论，首次建立了偏心转动及动载工况下三环减速器油膜浮动的流体动力润滑方程，为其动力学研究奠定了基础。

采用多重网格方法和Simpson积分公式对两级三环减速器油膜浮动均载时的承载能力进行了计算，计算结果为油膜浮动均载机构参数设计奠定了基础。

上一页

下一页