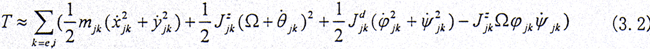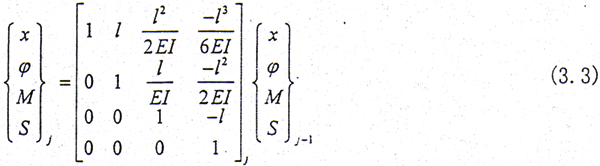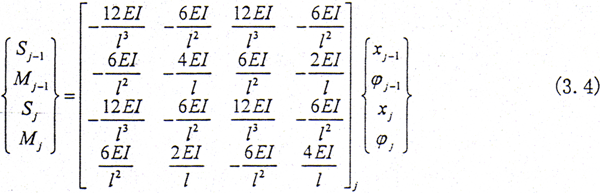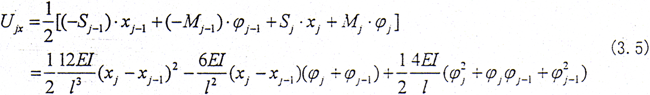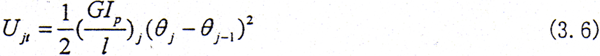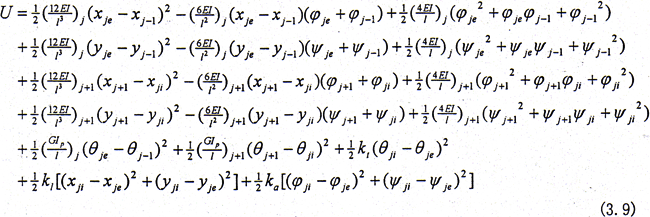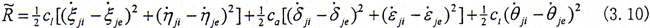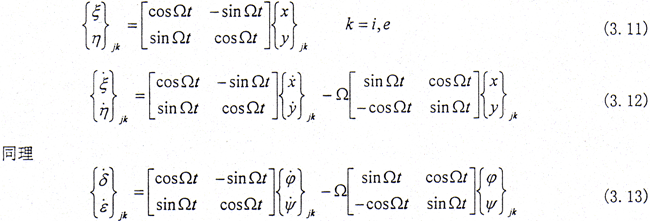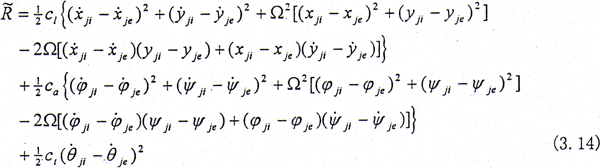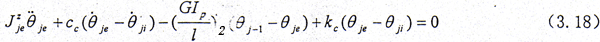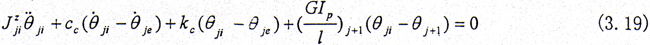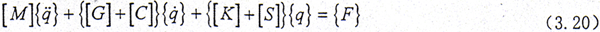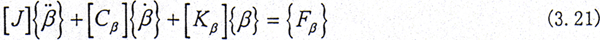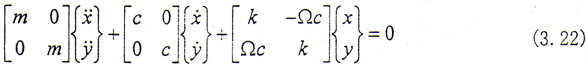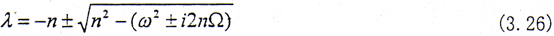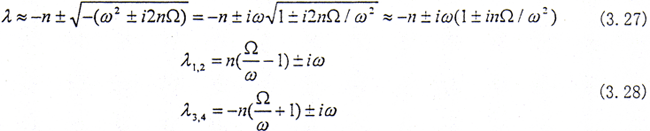第三章 对中齿轮联轴器系统的弯曲振动和扭转振动
3.1 引言
齿轮联轴器内外齿轮轴线在对中和不对中二种情况下,由于内外齿轮轮齿的接触状态不同,使得由齿轮联轴器连接的转子系统的运动形式存在差异。从理论上讲,轴线严格对中,则各齿上的受力和变形完全相同,因而在齿轮联轴器横向上的力学特性也完全相同[34];而在不对中时,则正好相反,因此相应的力学模型也会有所不同。本章在上一章的基础上,首先根据拉格朗日方程重点来讨论半齿轮联轴器在对中时,系统运动微分方程的建立过程,然后对一个由齿轮联轴器连接的二个Jeffcott转子所组成的系统(轴承—转子—齿轮联轴器系统)进行了比较详细的数值分析。有关齿轮联轴器在不对中时的建模和分析将在第五、第六、第七章中作详细的讨论。
在轴承—转子—齿轮联轴器系统的建立过程中要涉及到轴承、转子和齿轮联轴器这三部件的模化。在以小扰动为基础的线性系统中,一般将滑动轴承的油膜力用八个线性化的刚度和阻尼系数来表征;而将转子离散成为多个无质量的弹性轴段及具有质量和转动惯量的多个刚性圆盘,主要的方法有集总参数法和有限元法,具体的作法参见文献[90]。齿轮联轴器作为整体系统的一个子系统,一般有二对齿数相等内外齿相啮合的齿轮和相应的轴段组成,这样自然可以将其视为简单的轴般结构,将其中齿轮及轴段的质量和转动惯量分别等效到相应的结点上,齿轮啮合处的力学模型由上一章的六个刚度和阻尼系数给出。由于二对齿轮的啮合建模完全类似,所以在此我们重点来讨论一对啮合的齿轮处,即半齿轮联轴器系统的建模问题。并以此模型从理论上探讨轴承—转子—齿轮联轴器系统的失稳机理。通过数值方法分析齿轮联轴器对整体系统失稳转速的影响,并着重与等效轴计算方法[6]进行比较。计算了在多种工况下系统的临界转速和不平衡响应。
3.2 半齿轮联轴器系统运动方程
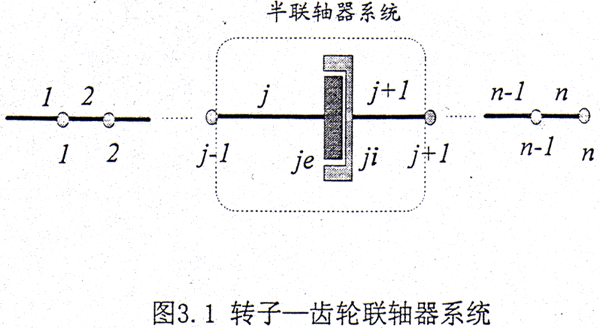
设将整个轴承—转子—齿轮联轴器系统划分成n个轴段和n个结点,在第j个结点处存在一个半齿轮联轴器系统,如图3.1所示。将外齿轮和内齿套均看作一当量圆盘,并满足小扰动假设,不计轴向运动,则圆盘的运动可用其中心的位移(xj,yj)和相应的偏转角(φj,ψj,θj)来表示,其中三个偏转角的意义见图3.2。设oxyz为固定坐标系,oξηz为相应的旋转坐标系,下面就以此为模型用拉格朗日方程来建立该子系统的运动微分方程。

3.2.1 动能
半齿轮联轴器系统的动能包括内齿套和外齿轮的平动动能和转动动能
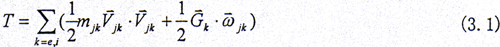
下标i,e分别表示内齿套和外齿轮。
对于半齿轮联轴器系统,内齿套和外齿轮的齿数是相等的,因此绕转轴的转动角速度均为Ω加上一个相应的小量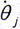 ,在小偏离的情况下,略去高阶小量后得系统的动能[90]为
,在小偏离的情况下,略去高阶小量后得系统的动能[90]为
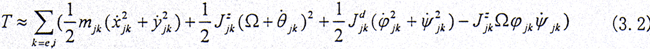
其中 Ω为转子的转动角速度;
mjk (k=e,i)分别为外齿轮和内齿套的质量;
Jljk(k=e,i l=d,z)分别为外齿轮和内齿套的赤道转动惯量和极转动惯量。
3.2.2 弹性势能
(1)轴段的弯曲弹性势能,参见图3.3。
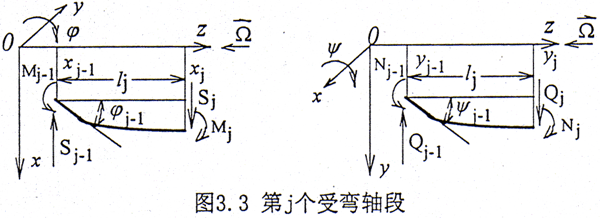
其中 Sj-1,Mj-1,Nj-1,Sj,Mj,Qj,Nj分别为作用于第j-1、j个结点处轴截面上的剪力和弯矩,根据平衡方程则第j个轴段在x方向
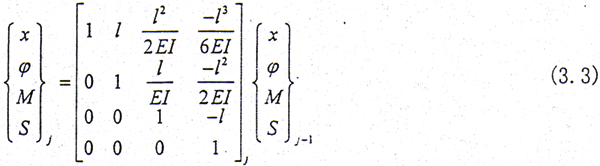
式中 EI为轴段截面的抗弯刚度。
由式(3.3)可得
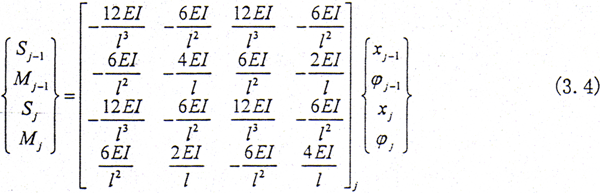
第j个轴段在x方向的弯曲弹性势能[91]
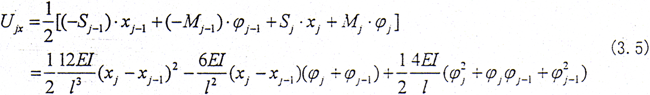
同理可得y方向的弯曲弹性势能。
(2)轴段的扭转弹性势能,参见图3.4。
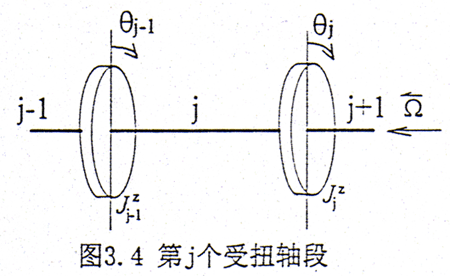
第j个轴段的扭转弹性势能
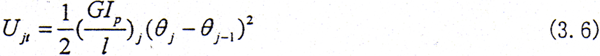
式中 GIp为轴段截面的抗扭刚度。
(3)半齿轮联轴器系统的弹性势能
第j个轴段的总弹性势能
Uj=Ujx+Ujy+Ujt (3.7)
半齿轮联轴器系统的弹性势能包括左右轴段和联轴器的弹性势能
U=Uj+Uie+Uj+1 (3.8)
将以上各式代入即得
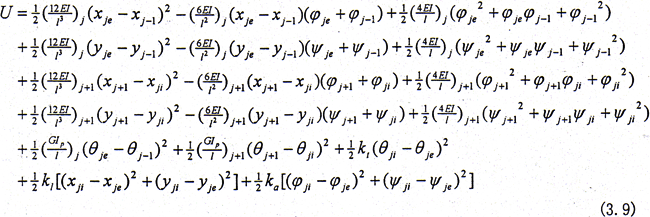
3.2.3 耗散函数
系统的能量耗散主要来自轴承的油膜阻尼和齿轮联轴器的内阻尼。在此暂不考虑轴承的油膜阻尼部分,对于联轴器的内阻尼所耗散的能量是与联轴器内外齿轮的相对运动有关,因此建立耗散函数时,应该在旋转坐标系中。半齿轮联轴器系统的耗散函数为
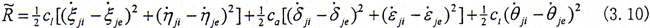
由图3.2中的坐标变换可得
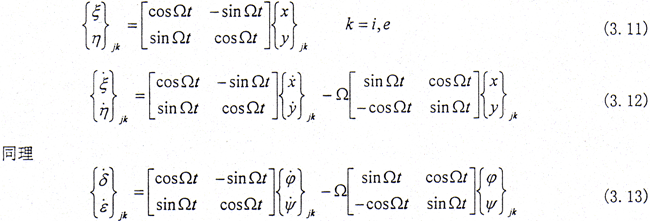
将式(3.12)、(3.13)代入式(3.10)中得
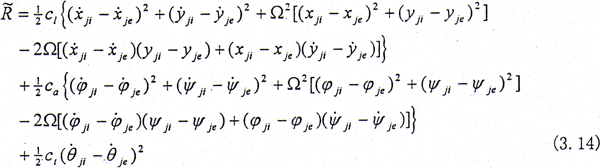
3.2.4 运动微分方程
根据拉格朗日方程

将式(3.2)、式(3.9)和式(3.14)分别代入式(3.15),就可以得到系统的运动方程。由于弯曲运动和扭转运动不耦合,所以将二者分开以便于讨论。
(1)半齿轮联轴器的弯曲运动方程
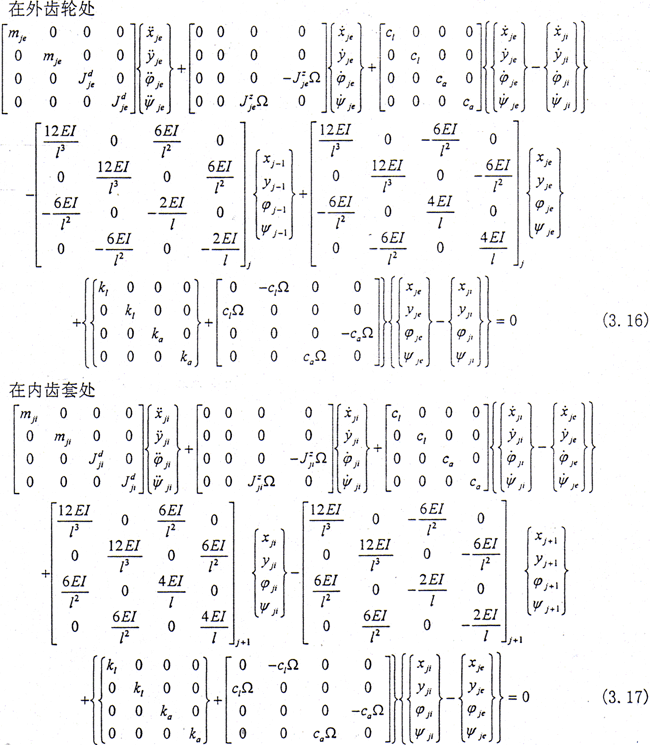
这样就得到了第j个结点(外齿轮、内齿套)处的弯曲运动微分方程。
(2)半齿轮联轴器的扭转运动方程
在外齿轮处
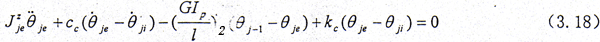
在内齿套处
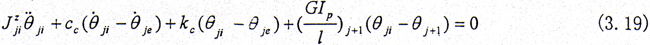
3.3 轴承—转子—齿轮联轴器系统的运动微分方程
(1)系统的弯曲运动微分方程
转子上各结点处(1,2,…,j-1)的弯曲运动微分方程可参见文献[90]。将上面推得的第j个结点(即半齿轮联轴器处)的弯曲运动微分方程合在一起就可以得到转子—齿轮联轴器系统的弯曲运动微分方程。如果在转子的第i个结点处具有滑动轴承支承,则只要在第i个结点处的运动方程中直接加入反应轴承的八个油膜刚度和阻尼系数,这样就可以得到整体系统的轴承—转子—齿轮联轴器耦合系统的弯曲运动微分方向,简写成
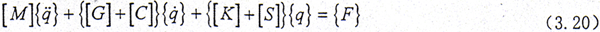
式中 {q}={x1 y1 φ1 ψ1 … xje yje φje ψje xji yji φji ψji … xn yn φn ψn}T
在式(3.20)中,[M],[C],[K]分别为整体系统的广义质量、阻尼和刚度矩阵,这三个矩阵是对称阵;而[G]是陀螺力阵,[S]是广义循环力(或称之为广义约束阻尼力)阵,这二个矩阵是反对称阵;{F}为外激振力阵。
(2)系统的扭转运动微分方程
同理可以写出转子上各结点处(1,2,…,j-1)的扭转运动方程,参见文献[90]。再将上面得到的第j个结点(即半齿轮联轴器处)的扭转运动微分方程合在一起就可以得到整体系统的扭转运动微分方程。简写为
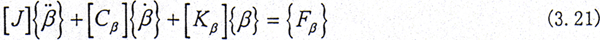
式中 {β}={θ1 … θie θii … θn}T;
[J],[Cβ],[Kβ]分别为系统的转动惯量阵,扭转阻尼力矩和扭转刚度阵;
{Fβ}为外扭转激振力矩阵。
由于扭转振动的内阻尼不存在自激,所以下面我们重点讨论整体系统的弯曲振动。
3.4 齿轮联轴器内阻尼引起自激振动的机理
在单自由度系统中,自激振动是由于负阻尼作用引起的,而在多自由度系统中就要复杂得多。并非一定象单自由度系统那样纯粹出于负阻尼,也可能由于各自由度之间的耦合作用引起不稳定振动。
对于具有内阻尼的简单耦合系统
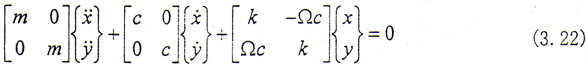
设方程的解为

则式(3.22)的特征方程为
(mλ2+cλ+k)2+(Ωc)2=0 (3.24)
令
2n=c/m, ω2=k/m (3.25)
则方程的特征值为
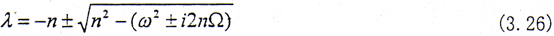
一般而言n=c/2m是很小的,故有
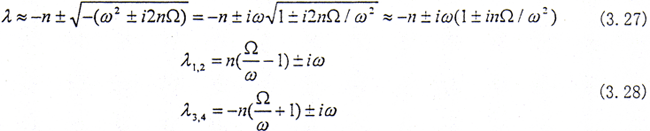
从λ1,2可以看出,在转子系统中,当Ω/ω>1,即转子的转动角速度大于系统的固有频率值时,则由{x y}T={X Y}Ten(Ω/ω-1)t·eiωt组成的振幅随时间增大,并以eiωt的形式振动,这样振动随时间不断的增大,即产生自激振动。因此在转子的转动角速度Ω大于系统的固有频率时,系统便会发生频率为ω的自激振动,并且随着Ω的增大(指超过ω后),系统的振动越来越敏感,这就是内阻尼引起自激振动的机理。当然在Ω/ω>1时,实际系统并不立即失稳,因为此时系统的非线性特性会显现出来,在此我们不作讨论。
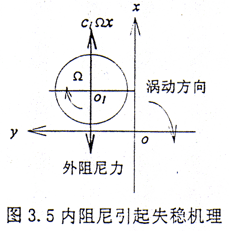
对于式(3.20)的稳定性分析要复杂得多,形如式(3.14)的耗散函数首见于文献[92]。美国学者Kane等在研究耗散的重力定向自旋卫星稳定性时发现的,与之相关的力被后来的学者称之为约束阻尼,并沿用至今,而在转子动力学中则多被称为循环力[93].如果在系统运动方程中没有循环力阵[S],则系统的稳定性可以利用著名的Kelvin-Tait-Chetaev定理来分析,但是当[S]≠0时,这个定理就不适用了。Mingori[94]、李俊峰等[95]对此作了专门的研究,给出了在某些特定条件下的判稳方法。文献[94]仍要求解一同阶矩阵的特征值;而文献[95]中的条件则要求det[G]≠0,因而式(3.20)不满足,比较可行的方法是运用Routh-Hurwitz法来判稳,但也只能解决低阶系统,对于高阶系统只能进行数值计算。一个比较简单的物理解释是在式(3.16)和式(3.17)中,存在首促进涡动的耦合力(clΩx)和耦合力矩(caΩφ)项。下面以耦合力(clΩx)为例来加以说明。设转子的转动方向和涡动方向如图3.5所示,耦合力与轴的转动方向相同,并且随转子转动角速度Ω的增大而增大,在Ω高于某一极限值时,这个耦合力会超过外阻尼使轴心产生一个与该力同向的加速度,这个加速度使轴心轨迹发散,即系统失稳。
实际上从式(3.16)和式(3.17)可知,由于联轴器的内阻尼使方程的最后一项产生交叉耦合并呈反对称,而正是此项的出现会降低系统的稳定性,这也是转子动力学中内阻尼引起的各种自激振动的共同特性。
上一页
下一页



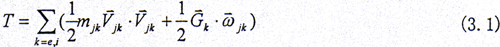
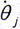 ,在小偏离的情况下,略去高阶小量后得系统的动能[90]为
,在小偏离的情况下,略去高阶小量后得系统的动能[90]为