3.5 无量纲化
在工程分析计算中,位移、时间和力是基本量,其它是导出量,因此各无量纲化定义如下:
无量纲位移:Xj=xj/d0,Yj=yj/d0,Ljlj/d0,Dj=dj/d0;
无量纲时间:τ=Ωt;
无量纲剪力: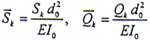
无量纲力矩: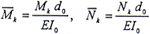
无量纲质量和转动惯量: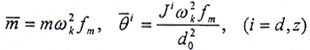
无量纲刚度系数: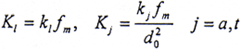
无量纲阻尼系数: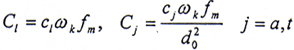
无量纲转动角速度: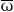 =Ω/ωk;
=Ω/ωk;
其中:ωk为一阶临界转速;
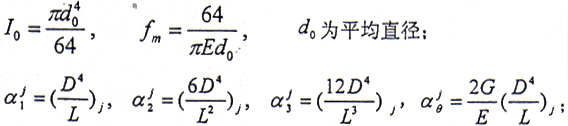
设系统方程的解为:x=x0eλt,λ=-u+iv;
则相应的无量纲表达式为: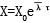 ;
;
式中: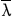 =λ/Ω=-U+iV,而 U=u/Ω,V=v/Ω。
=λ/Ω=-U+iV,而 U=u/Ω,V=v/Ω。
经上述过程后,将式(3.20)和式(3.21)无量纲化,就可以方便地写出无量纲形式的系统运动微分方程。限于篇幅在此从略。
3.6 系统方程的求解
当{F}=0时,式(3.20)为自由振动方程,可以对系统进行模态分析。此时式(3.20)所对应的特征值问题为
(λ2[M]+λ([G]+[C])+[K]+[S]){φ}=0 (3.29)
这是一个二次特征值问题,可以化为一般的广义特征值问题求解。求解的方法有QR法、Lanczos法和广义逆迭代法等,本文采用广义逆迭代法[90]。
当{F}≠0时,可以对系统进行各种强迫振动分析。在转子系统中,最主要的外激振力是转子的不平衡而引起的惯性力,因此只要确定了转子的不平衡量及其作用的位置,就可以计算系统的不平衡响应,常用的方法有振型叠加法、直接积分法和高斯消去法[90]。本文采用高斯消去法直接求解系统的不平衡响应。
3.7 轴承—转子—齿轮联轴器系统的动力学分析
轴承—转子—齿轮联轴器系统的动力学分析包括系统的稳定性和模态分析以及临界转速和不平衡响应的计算等内容。下面主要来讨论齿轮联轴器的动力特性对系统的影响。
计算模型如图3.6所示。整体系统由一个齿轮联轴器连接的二个Jeffcott转子系统所组成,共有三跨,因此是一典型的多跨轴承—转子系统。齿轮联轴器的结构近似选用CL5型,为方便问题的讨论,重点分析左右对称布置的系统。系统具体的结构参数见表3.1。工作转速为n=3000rpm。齿轮联轴器对中良好,全齿宽接触。计算采用无量纲化(在后面的计算中,如无特殊说明均为无量纲)。传统上计算此类问题时往往采用两种方法,第一种方法是将联轴器人为截断,只计算系统的左侧或右侧转子[18,50],即单轴分析法,这样系统为一单跨轴承—转子系统,系统静定负荷分配简单,但是却忽略二转子之间的耦合作用;第二种方法是整体分析法,这一方法是将整个系统作为研究对象,将齿轮联轴器用一等效的轴段[6]来代替(故称之为等轴法),等效轴段长度的刚度即为等效刚度,此时系统是超静定的。从直观上看这样处理似乎比单轴分析法更为合理,但是其中等效轴段的长度不易确定。为便于比较在下文中凡涉及到等效轴法的计算结果均是以联轴器的实际长度作为等效长度而得的。
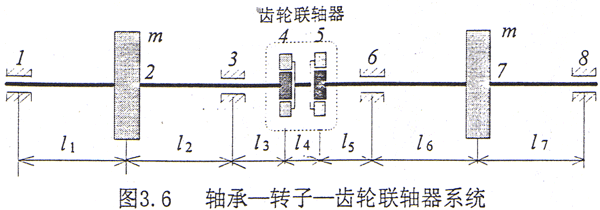
表3.1 对称转子系统的结构参数
| 轴段及材料 |
圆盘 |
圆轴承 |
| li=0.5m(i=1,2,6,7) |
轴径 d=0.09m |
质量 m=700kg |
长径比 B/d=0.5 |
| l3=l5=0.15m |
弹性模量E=206GPa |
极转动惯量Jz=12.0kg·m2 |
间隙比 ψ=0.2% |
| l4=0.15m |
泊松比 μ=0.3 |
赤道转动惯量Jd=6.0kg·m2 |
动力粘度μ=0.0221Pa·s |
3.7.1 齿轮联轴器对轴承特性的影响
对于对称轴承—转子—齿轮联轴器系统,计算步骤如下:1)轴心的平衡位置随转速的变化关系,结果如图3.7所示。2)轴承的油膜刚度和阻尼系数随转速的变化关系,结果如图3.8所示。由于在两侧转子上对应轴承的特性相同,故仅列出在左侧转子上二个轴承(#1和#2)处的结果。
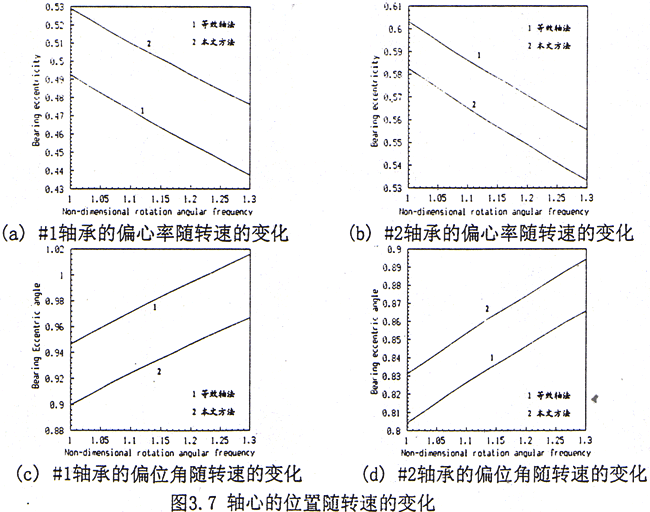
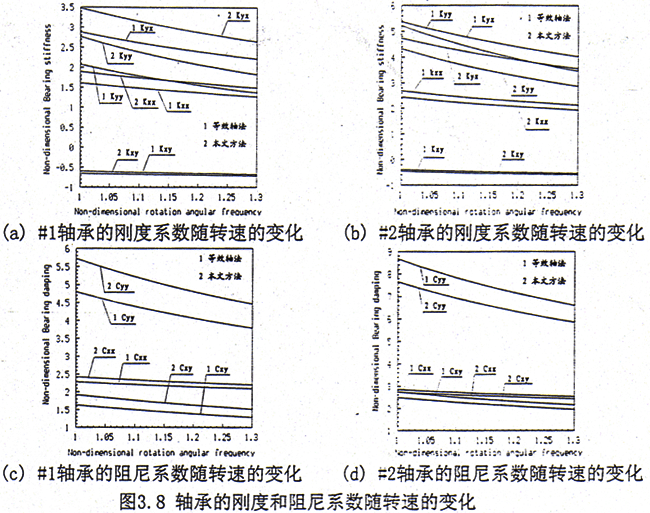
从以上的计算结果来看,用等效轴法计算轴承的轴心位置,#1轴承处的偏心率明显偏小,偏位角偏大,而在#2轴承处则正相反。这表明采用等效轴法会使转子的平衡位置产生较大的误差,也预示着#1轴承和#2轴承之间负荷分配的变化。另外比较#1和#2轴承的结果,还可以看出,联轴器的作用使得二个轴承的负荷分配趋于接近,而等效轴法从某种意义上讲相当于二个转子的直接对接,必将造成二轴承负荷分配不均,在工作转速下各轴承处的负荷分配见表3.2,因此对轴承的受力来说这也正是采用齿轮联轴器的优点所在。从二轴承处的动特性来看,#1轴承的各项刚度和阻尼系数比等效轴法大,而#2轴承的各项刚度和阻尼系数则比等效轴法小,这归根到底也是轴承负荷分配发生了变化的结果。如果采用单轴分析方法计算,以左侧转子为例,由于联轴器的质量与圆盘相比要小许多,系统近似为一对称转子系统,则作用在#1和#2轴承上的负荷相差不大,因此二个轴承处的动特性系数也比较接近。由于轴承的静、动特性发生了变化,因此势必引起系统动态特性的变化。
表3.2 工作转速下各轴承处的负荷分配(kg)
| |
#1轴承 |
#2轴承 |
#3轴承 |
#4轴承 |
| 本文方法 |
311.55 |
414.45 |
414.45 |
311.55 |
| 等效轴法 |
259.64 |
465.17 |
465.17 |
259.64 |
3.7.2 齿轮联轴器对系统复特征值和复模态的影响
下面对二侧对称的轴承—转子—齿轮联轴器系统进行分析计算。
(1)按‘等效轴’法计算,结果见表3.3。
表3.3 按‘等效轴’法计算得不同转速下系统的特征值
| 相对工作角速度Ω/ωk |
No. |
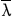 i=u/Ω+iv/Ω i=u/Ω+iv/Ω |
| 1.00000 |
1
2
3
4 |
-0.34774D-01+i0.72585D+00
-0.22925D-01+i0.76828D+00
-0.41981D-01+i0.83403D+00
-0.28089D-01+i0.85016D+00 |
| 1.43719 |
1
2
3
4 |
-0.83590D-05+i0.51463D+00
-0.15650D-02+i0.53676D+00
-0.27019D-01+i0.57455D+00
-0.23805D-01+i0.58722D+00 |
| 1.43819 |
1
2
3
4 |
0.35243D-04+i0.51430D+00
-0.15355D-02+i0.53639D+00
-0.26998D-01+i0.57414D+00
-0.23797D-01+i0.58681D+00 |
注:ωk=314.159 rad/s(不同)。
(2)不计齿轮联轴器内阻尼按本文方法计算,结果见表3.4。
表3.4 不同转速下轴承—转子—联轴器系统的特征值
| 相对工作角速度Ω/ωk |
No. |
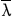 i=u/Ω+iv/Ω i=u/Ω+iv/Ω |
| 1.00000 |
1
2
3
4 |
-0.19310D-01+i0.63059D+00
-0.14980D-01+i0.64585D+00
-0.18366D-01+i0.72318D+00
-0.65746D-01+i0.80639D+00 |
| 1.26417 |
1
2
3
4 |
-0.14454D-04+i0.50838D+00
-0.44376D-03+i0.51607D+00
-0.16639D-01+i0.57032D+00
-0.57178D-01+i0.62901D+00 |
| 1.26517 |
1
2
3
4 |
0.35627D-04+i0.50801D+00
-0.40779D-03+i0.51568D+00
-0.16633D-01+i0.56986D+00
-0.57150D-01+i0.62848D+00 |
比较上述二种情况,可以看出在工作转速Ω/ωk=1.0时,表3.3所列系统低阶特征值的实部和虚部的绝对值明显要大于表3.4所对应的值,这表明:1)在正常工作状态下,按等效轴法计算得的系统对数衰减率和固有频率要大。按等效轴法计算,在Ω/ωk=1.43819时系统失稳;而按本文的模型,即使在全齿宽接触的情况下,系统的失稳转速也只为Ω/ωk=1.26517,这说明用等效轴法来计算这类系统的失稳转速,数值明显偏高,是极不合适的。2)通过比较Ω/ωk=1.0时,低阶固有频率值的数值可以推出,按等效轴法所计算得的系统的低阶临界转速也是偏高的,这一现象在一实际的轴承—转子—齿轮联轴器系统中被证实[66],因为等效轴法实质上相当于齿轮联轴器被锁定时将二个转子看成为一个整体,这样处理相当于给系统增加了一个约束,结果自然会失真。关于系统的临界转速在后面我们还将作详细的讨论。如果按单轴分析法计算,系统的失稳转速Ω/ωk=1.19215。因此用等效轴法(按联轴器的实际长度作为等效长度)和单轴分析法所计算得的系统失稳转速实质上是二个极限,前者偏高不安全,而后者偏低过于保守。
(3)齿轮联轴器的内阻尼对系统失稳转速的影响
齿轮联轴器的内阻尼系数可由上一章的方法计算。总的来说,联轴器的内阻尼受系统工况的影响较大,在不同的工况下内阻尼会有所变化。设各齿承载相同,即联轴器对中良好,其中扭矩T取为CL5型齿轮联轴器许用扭矩的一半;按照文献[34],齿面间的滑动摩擦系数取为f=0.15;ω应为转动角速度与最易产生失稳的涡动角速度之差,失稳一般首先发生在低阶,在此涡动频率取为第一阶固有频率。相对横向振幅为CL5型联轴器[88]内外齿轮之间的径向间隙c,相对转角振幅为arctg2c/l,其中l为内外齿轮的接触宽度。这样可以计算得到在工作转速下无量纲内阻尼系数为Cl=0.38,Ca=3.67×10-3。系统的失稳转速见表3.5。
表3.5 不同转速下轴承—转子—联轴器系统的特征值
| 相对工作角速度Ω/ωk |
No. |
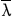 i=u/Ω+iv/Ω i=u/Ω+iv/Ω |
| 1.00000 |
1
2
3
4 |
0.19315D-01+i0.63062D+00
-0.14968D-01+i0.64611D+00
-0.19918D-01+i0.72273D+00
-0.66795D-01+i0.80548D+00 |
| 1.26317 |
1
2
3
4 |
0.21974D-04+i0.50879D+00
-0.14346D-03+i0.51674D+00
-0.18046D-01+i0.57034D+00
-0.57988D-01+i0.62870D+00 |
| 1.26417 |
1
2
3
4 |
0.30147D-04+i0.50842D+00
-0.10558D-03+i0.51636D+00
-0.18039D-01+i0.56988D+00
-0.57959D-01+i0.62818D+00 |
比较表3.4和表3.5二种情况,系统的失稳转由1.26517降为1.26417,显然变化很小。而且失稳时的涡动频率也几乎不变。如果将各内阻尼系数增大为原来的5倍,则失稳转速在ω/ωk=1.23417~1.23517之间。由此可见,在对中良好并且内外齿轮间润滑充分时,联轴器内阻尼对系统失稳转速的影响不十分明显。当然在润滑失效并且对中不良时,由于偏载效应而引起齿面间的摩擦力(力矩)可能要大得多[6],此时内阻尼系数也会相应增大。
(4)齿轮联轴器耦合系统的复模态
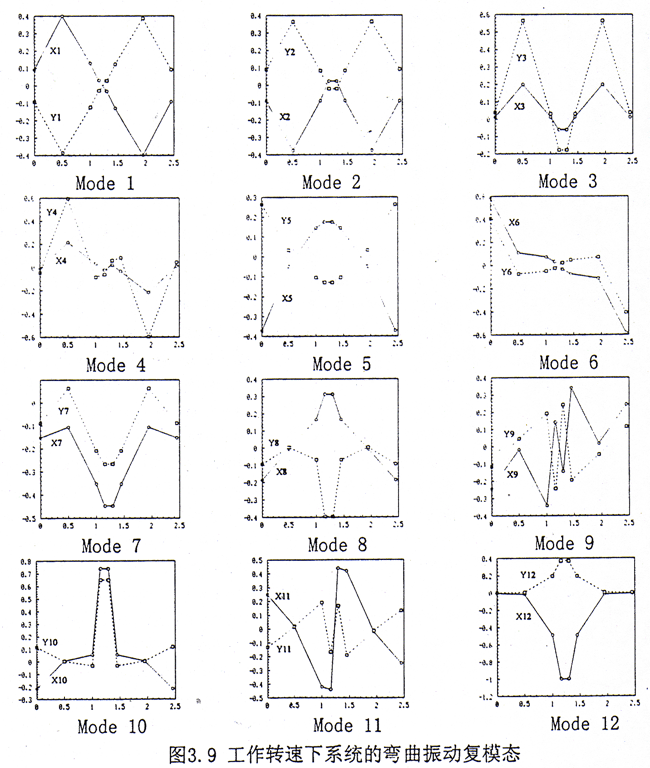
在ka=0.128不计内阻尼时,工作转速下系统的前12阶弯曲振动复模态图见图3.9。从复模态图上可以看出,在低阶弯曲模态中,轮齿的变形是较小的,轮齿变形较大主要发生在高阶模态中。这与实际情况比较接近,因为在实际的转子系统中,轮齿的刚度一般比轴段的刚度要大许多,因此在低阶的弯曲模态中,轮齿的变形体现不出来。系统前2阶的扭转振型如图3.10所示。在前二阶扭转振型中轮齿变形也较小。

上一页
下一页

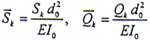
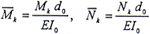
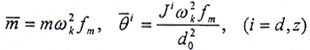
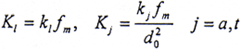
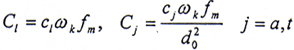
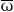 =Ω/ωk;
=Ω/ωk;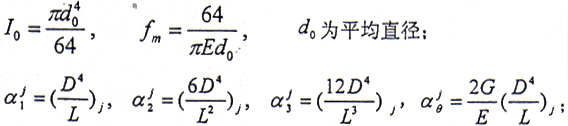
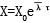 ;
;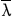 =λ/Ω=-U+iV,而 U=u/Ω,V=v/Ω。
=λ/Ω=-U+iV,而 U=u/Ω,V=v/Ω。



