3.7.3 齿轮联轴器刚度和阻尼的变化对系统稳定性的影响
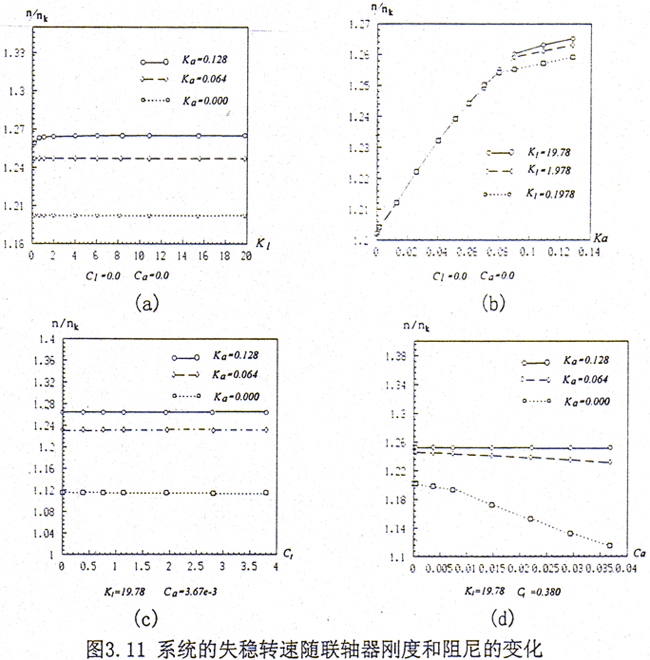
(1)齿轮联轴器的刚度对系统失稳转速的影响
从图3.11a可见随横向刚度的增大系统的失稳转速几乎没有变化,只有在转角刚度较大而且横向刚度较小时,系统的失稳转速才有所变化。图3.11b表示系统失稳转速随转角刚度的变化,系统的失稳转速随转角刚度变化显著。在转角刚度较小时,几乎是线性增加。当转角刚度达到某一值时,失稳转速变化趋缓。进一步的计算表明,当继续增大转角刚度,系统的失稳转速趋于一定值。原因是当转角刚度增大到某值时,在齿轮啮合处已接近于一刚性连接的结构,如果继续增大转角刚度则对整体系统的刚度影响不大,因此系统的失稳转速变化不大。对齿轮联轴器而言,一般横向刚度是比较大的,因此对系统的失稳转速的影响可不予考虑。在转角刚度较小时,系统的失稳转速随转角刚度的增加而增加,所以转角刚度对系统的失稳转速影响必须予以考虑。转角刚度与轮齿有效接触齿宽b的平方成正比,而有效接触齿宽b主要与联轴器的齿形和内外齿间的接触情况有关,一般而言b值较少,对于修形齿和鼓形齿则更小。关于轮齿的接触情况则比较复杂,当不考虑轮齿的误差时,则主要受工况的影响,不同的工况接触情况不同,即使在同一工况下也会有所变化,因此对于具有情况应区别对待。
(2)齿联轴器的内阻尼对系统失稳转速的影响
从图3.11c可见在一定的范围之内,齿轮联轴器横向内阻尼的变化对系统的失稳转速几乎没有影响。由图3.11d可知,随齿轮联轴器转角内阻尼的增加失稳转速减小,减少的幅度与系统的转角刚度有关,转角刚度取大值时,系统的失稳转速变化甚微,而取小值时,则变化明显。一般而言,对于确定的齿轮联轴器类型,如果轮齿间的润滑充分对中良好,则转角内阻尼变化不会太大。所以系统的失稳转速也不会有明显的变化。但当润滑不充分,齿轮联轴器对中不良时,转角内阻尼的变化较大,从而会引起系统失稳转速生产较大的变化。
从以上的计算分析可以推出,在工作转速下,由于齿轮联轴器的刚度和内阻尼的影响,会对系统的对数衰减率产生影响,其中尤以联轴器的转角刚度影响最为显著,究其根本原因是联轴器的转角刚度对系统的负荷分配产生影响,从而引起轴承特性的变化进而影响系统的稳定性。对于实际的轴承—转子系统,在轻载时,由于传递的扭矩较小,引起内外齿轮之间的摩擦力和摩力矩较小,但此时内外齿轮之间的有效接触长度也较小,这样联轴器的转角刚度变小,因此容易引起系统的不稳定。而在重载时,内外齿轮之间的有效接触长度变大,转角刚度随之迅速增大,此时虽然摩擦也有所增大,但就总体而言系统的失稳反而有可以不易发生。
传统认为齿轮联轴器对轴承—转子系统稳定性的影响主要是由于它的内摩擦或内阻尼特性。通过以上的分析,可以得出这样的结论:齿轮联轴器对系统稳定性的影响,是其动力特星的综合反应,并非只是其中的内阻尼。从影响的程度来看,以转角刚度影响最大;在一定的条件下转角内阻尼也会产生一定的影响,即作用于联轴器上的弯矩是影响系统稳定性的主要原因。横向刚度和横向内阻尼对系统的稳定性影响不大,即作用于联轴器上的横向剪切作用可以不计。
3.7.4 转子外伸端的几何参数对系统稳定性的影响
在实际的转子系统设计中,外伸端的长度是一个重要的几何参数,文献[5]认为应该尽量取短一些。下面仍以上述系统进行计算,其中取无量纲值Kl=19.78,Ka=0.128。不考虑联轴器内阻尼,其它参数不变。表3.6列出图3.6所示轴承—转子—齿轮联轴器系统在外伸端长度增大一倍时,#1轴承和#2轴承的刚度和阻尼系数。
| |
Kxx |
Kxy |
Kyx |
Kyy |
Cxx |
Cxy |
Cyx |
Cyy |
| No.1 |
1.9007
(1.8926) |
-0.5923
(-0.5942) |
3.4990
(3.4810) |
2.7885
(2.7668) |
2.4288
(2.4244) |
1.9343
(1.9260) |
1.9343
(1.9260) |
5.7537
(5.7260) |
| No.2 |
2.4342
(2.4420) |
-0.4567
(-0.4544) |
4.7201
(4.7393) |
4.3122
(4.3377) |
2.7243
(2.7285) |
2.4851
(2.4932) |
2.4851
(2.4932) |
7.6293
(7.6589) |
*注:括号()内的值为L3=L5=1.67时,相应的轴承动特性系数。
比较表3.6中的数值,增加外伸端的长度使#1轴承的油膜刚度系数和阻尼系数增大,而#2轴承的油膜刚度系数和阻尼系数则相应地要减小。从理论上讲,对于这类转子系统(以图3.6中齿轮联轴器左侧的轴承—转子为例)是一典型的外伸梁结构,如果改变外伸端的长度,将使#1轴承和#2轴承的负荷分配发生变化,进而影响轴承的动特性系数。但一般而言,转子系统的质量要元大于联轴器的质量,因此外伸端长度的改变对轴承的负荷分配影响不大,因此动特性系数的变化也不大。
表3.7是转子外伸端的长度增加一倍时各转速下系统的复特征值。从中可以看出系统的失稳转速虽然减小,但减小不多。对低阶特征值影响不大,但对高阶特征值有一定的影响。在实际工程中,许多系统失稳首先在低阶发生,此时适当改变外伸的长度不会对系统的稳定性产生明显影响;而当系统失稳有可能在较高阶发生时,增加外伸端长度会对系统的稳定性产生不利影响。
表3.7 L3=L5=3.33时系统的特征值
| 相对工作角速度Ω/ωk |
No. |
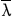 i=u/Ω+iv/Ω i=u/Ω+iv/Ω |
| 1.00000 |
1
2
3
4 |
-0.13644D-01+i0.63999D+00
-0.17115D-01+i0.71224D+00
-0.19071D-01+i0.72955D+00
-0.46959D-01+i0.82386D+00 |
| 1.26317 |
1
2
3
4 |
-0.29851D-04+i0.51157D+00
-0.26953D-02+i0.52827D+00
-0.15519D-01+i0.56229D+00
-0.44809D-01+i0.64717D+00 |
| 1.26417 |
1
2
3
4 |
0.47588D-05+i0.51119D+00
-0.26361D-02+i0.52789D+00
-0.15513D-01+i0.56184D+00
-0.44790D-01+i0.64663D+00 |
一些轴承—转子—齿轮联轴器系统为了降低左右转子间的耦合作用,将转子外伸端的直径缩小,下面对此作一简讨论。设系统的其它参数不变。外伸端的无量纲直径由原来的D3=D5=1.0变为D3=D5=0.667,即外伸端的直径减小到原来的三分之二。计算结果分别由表3.8和表3.9给出。
#1和#2轴承刚度和阻尼系数的变化趋势与增大外伸端的长度相同,变化幅度稍大。缩小转子外伸端的直径也使系统的失稳转速降低,降低的幅度也不很大,但转子直径的减小会严重影响到整体系统的扭转刚度和强度,因此在系统设计时应综合考虑各种因素的影响。
表3.8 D3=D5=0.667时轴承的动特性系数(n=3000rpm)
| |
kxx |
kxy |
kyx |
kyy |
cxx |
cxy |
cyx |
cyy |
| No.1 |
1.9582
(1.8926) |
-0.5790
(-0.5942) |
3.6262
(3.4810) |
2.9413
(2.7668) |
2.4609
(2.4244) |
1.9936
(1.9260) |
1.9936
(1.9260) |
5.9496
(5.7260) |
| No.2 |
2.3781
(2.4420) |
-0.4728
(-0.4544) |
4.5851
(4.7393) |
4.1343
(4.3377) |
2.6938
(2.7285) |
2.4271
(2.4932) |
2.4271
(2.4932) |
7.4220
(7.6589) |
注:括号()内的值为D3=D5=1.0时,相应的轴承动特性系数。
表3.9 D3=D5=0.667时系统的特征值
| 相对工作角速度Ω/ωk |
No. |
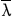 i=u/Ω+iv/Ω i=u/Ω+iv/Ω |
| 1.00000 |
1
2
3
4 |
-0.15511D-01+i0.62338D+00
-0.12541D-01+i0.63177D+00
-0.17169D-01+i0.70317D+00
-0.38389D-01+i0.74726D+00 |
| 1.24220 |
1
2
3
4 |
-0.42456D-04+i0.50905D+00
-0.22512D-03+i0.51325D+00
-0.15685D-01+i0.56461D+00
-0.34419D-01+i0.59737D+00 |
| 1.24320 |
1
2
3
4 |
0.42574D-05+i0.50867D+00
-0.18903D-03+i0.51285D+00
-0.15679D-01+i0.56415D+00
-0.34404D-01+i0.59688D+00 |
3.7.5 齿轮联轴器对系统临界转速的影响
文献[8]指出,在实际的大化肥透平压缩机组振动中,由于转子轴承系统临界转速计算不准确,安全裕度不足而产生共振的现象。这从一个侧面反映出这类系统的设计和计算存在问题。
经计算可知,联轴器的横向刚度、横向阻尼和转角阻尼对系统临界转速的影响不大,但转角刚度有较大的影响,在工作范围之内的临界转速见表3.10,其中包括了同步正向涡动和同步反向涡动时的临界转速。为便于比较,表3.10同时给出了用单轴分析法和等效轴法分析计算得到的系统的临界转速。从表中的数值来看,转角刚度Ka对系统的临界转速的影响是比较大的。总的来说,随转角刚度Ka的增大,各阶临界转速增大。Ka的取值与齿轮联轴器内外齿轮间的接触情况密切相关,在其它一些因素一定时,Ka取小值表示承载较小,而Ka取大值则表示承载较大,因此在具有齿轮联轴器耦合的系统中,临界转速会随工况的变化而发生变化。从表中还可以看出用单轴分析法和用等效轴法计算得的系统临界转速值分别是二种极限情况,用这二种方法进行分析计算会产生不小的偏差,而且也不能反应出工况的变化,因此在实际工程中,有可能出现转子系统的工作转速与临界转速之间裕度不足问题[8]。另外,实际系统是非常复杂的,即使同一类型的系统,也由于制造、安装等会引起Ka发生一定变化,从而也会引起系统临界转速发生变化。
在Ka=0.0和Ka=0.128二种工况下,计算了图3.6所示系统,转子外伸端几何参数变化对系统的临界转速的影响,结果分别见表3.11和表3.12。可以看出在同一工况下,临界转速变化不大。
表3.10 在工作转速范围之内的临界转速
| |
无量纲临界转速 |
| 单轴 |
0.6027 |
|
0.6690 |
|
| Ka=0. |
0.6030 |
0.6033 |
0.6660 |
0.6683 |
| Ka=0.008 |
0.6072 |
0.6091 |
0.6736 |
0.7034 |
| Ka=0.032 |
0.6123 |
0.6173 |
0.6877 |
0.7600 |
| Ka=0.128 |
0.6150 |
0.6450 |
0.7277 |
0.8167 |
| 等效轴法 |
0.6200 |
0.7236 |
0.8470 |
0.8590 |
表3.11 外伸端直径变化对临界转速的影响(D3=D5=0.667,L3=L5=1.67)
| |
无量纲临界转速 |
| Ka=0. |
0.6032 |
0.6033 |
0.6659 |
0.6683 |
| Ka=0.128 |
0.6128 |
0.6301 |
0.7064 |
0.7543 |
表3.12 外伸端长度变化对临界转速的影响(D3=D5=1.0,L3=L5=3.33)
| |
无量纲临界转速 |
| Ka=0. |
0.5996 |
0.6007 |
0.6508 |
0.6611 |
| Ka=0.128 |
0.6393 |
0.6410 |
0.7156 |
0.8320 |
3.7.6 齿轮联轴器对系统不平衡响应的影响
设仅在左侧圆盘处存在一质量偏心,其中无量纲偏心距为1.1×10-4。在4个轴承处的不平衡响应如图3.12所示。

用单轴分析法计算不平衡响应,在#1和#2轴承上产生的振幅最大,等效轴法则最小,而在#3轴承和#4轴承上产生的振幅则正相反。其中用单轴分析法计算不平衡响应,在#3和#4轴承处不产生振动,这与实际情况不符;用等效轴法计算,则明显夸大了二侧转子的耦合作用,没有体现出齿轮联轴器的特点。因此采用单轴分析方法和等效轴方法计算系统的不平衡响应均存在不小的误差。通过上面的计算可见,随着转角刚度的增大,左侧转子的不平衡量对本身转子支承轴承所激起的响应幅值明显减小,对右侧转子支承轴承所激起的响应幅值则明显增大。
系统其它的参数不变,仅改变转子外伸端的几何参数,计算结果见图3.13。图中符号的意义如下:1—D3=D5=1.0,L3=L5=1.67,即悬臂端的直径和长度均保持不变;2—D3=D5=0.667,L3=L5=1.67,即悬臂端的直径减小,长度不变;3—D3=D5=1.0,L3=L5=3.33,即悬臂端的直径不变,长度增大。
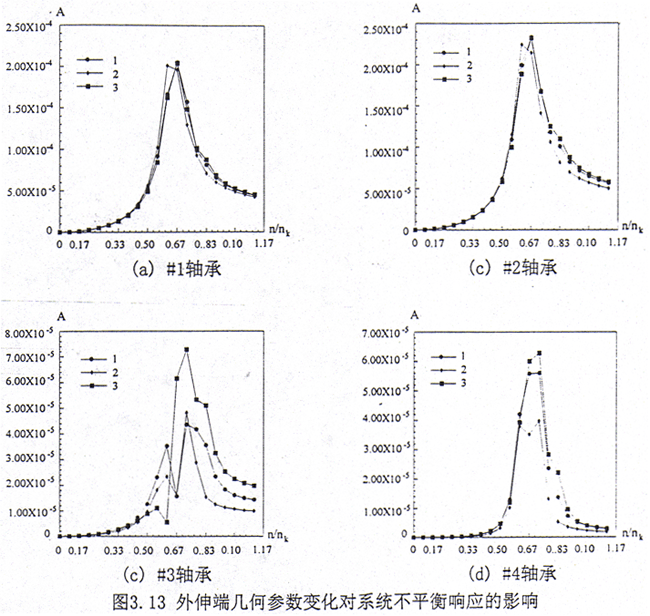
从上面的计算可见,在给定的条件下,转子外伸端的几何参数对在#1、#2轴承处的不平衡响应影响不大;对#3、#4轴承处的不平衡响应有影响,但量级较小,因此可以认为外伸端的几何尺寸对系统的不平衡响应影响较小。
3.8 小结
本章根据拉格朗日方程,完整地推导了齿轮联轴器在对中时,轴承—转子—齿轮联轴器系统的运动微分方程,并从理论上阐明了齿轮联轴器的内阻尼引起自激振动的机理。应用上述模型对轴承—转子—齿轮联轴器系统进行了数值模拟,结论如下:
(1)用传统的单轴分析法和等效轴法来计算系统的失稳转速,结果会出现偏差。单轴分析法使失稳转速降低而偏于保守,等效轴法则偏高不安全。
(2)作用于齿轮联轴器上的弯矩是影响系统稳定性的主要原因。在对中良好并且润滑充分时,齿轮联轴器的横向刚度、横向阻尼和转角阻尼对系统的失稳转速影响不十分明显,而转角刚度对系统的失稳转速影响较大。
(3)用单轴分析法和等效轴法计算系统的临界转速和不平衡响应均会出现较大的误差。单轴分析法忽视了齿轮联轴器对二侧转子的耦合作用,而等效轴法则过分夸大了这种作用。
上一页
下一页


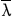 i=u/Ω+iv/Ω
i=u/Ω+iv/Ω
